프로그래머스 약수의 개수 구하기 자바

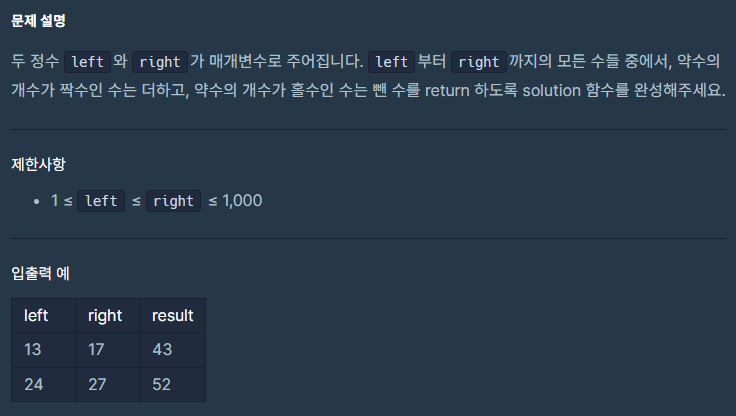
문제

풀이

class Solution {
    public int solution(int left, int right) {
        int answer = 0;
        for(int i = left; i <= right; i++){
            int cnt = 0;
            for(int y = 1; y*y <= i; y++ ){
                if(y*y == i){
                    cnt++;
                }else if(i % y == 0){
                    cnt+=2;
                }
            }
            if(cnt % 2 == 0){
                answer += i;
            }else{
                answer -= i;
            }
        }
        
        return answer;
    }
}

리뷰

약수의 개수를 구하기만 하면 되는 간단한 문제였다.
다만 약수의 개수를 구할 때 단순히 1에서부터 n까지 모든 수를 찾아가며 약수인지 검증을 하는데는 오랜 시간이 걸린다.
따라서 탐색의 범위가 클 경우 최적화하는 알고리즘이 필요하다.

먼저 n에 대한 약수의 개수를 찾고자 할 때, n의 제곱근까지만 구하면 모든 약수의 개수를 찾을 수 있다.
1부터 1씩 증가하는 i가 있을 때,

1. 'i * i == n'이라면 약수라는 뜻이므로 약수의 개수를 저장하는 변수 cnt에 1을 더한다.
2. 'n % i == 0'이라면 i가 n의 약수라는 뜻인데, 예를들어 14(n)라는 값에서 2(i)가 약수인데, 정확히는 2 * 7 = 14로 2와 7 두 숫자가 약수인 것을 알 수 있다.
   따라서 이 경우 cnt에 2를 더해준다.