[알고리즘] 7662 발표자료

요구사항

• 이중 우선순위 큐를 구현하는 것임.
• 필요한 것은

1. 데이터 구조
   1. 최대값과 최소값을 효율적으로 삭제할 수 있어야 한다
   2. 중복된 값도 저장가능
2. 연산
   1. I n
      1. 정수 n을 큐에 삽입
   2. D 1
      1. 큐에서 최댓값을 삭제함.
   3. D -1
      1. 큐에서 최솟값을 삭제함.
3. 기타
   1. 큐가 비어있는 경우 D 연산이 들어오면 무시
   2. 최대값이나 최솟값이 여러 개인 경우 하나만 삭제
   3. 모든 연산 처리 후 큐가 비어있다면 EMPTY
   4. 남아있는 값 중 최댓값과 최솟값을 출력

코드분석

• 트리 맵 사용
  • key 를 기준으로 정렬된 값을, 기준으로 log n 의 속도로 조회가 가능하다.
  • 근데 first key 나 last key 의 경우 상수시간에 조회가 가능함.
• 문제에서 최댓값과 최솟값만 빠르게 조회하면 되기에 트리맵이 가장 어울리는 자료구조였음.

Operation operation = Operation.findBy(st.nextToken());
int num = Integer.parseInt(st.nextToken());

• D 인지 I 인지 등.. 연산을 찾는다.
• num ← 은 삽입할 키값이다.

public enum Operation {
        INSERT("I"),
        DELETE("D"),
        ;
        
        private final String operation;
        
        Operation(String operation) {
            this.operation = operation;
        }
        
        public String getOperation() {
            return operation;
        }
        
        public boolean isDelete() {
            return this == DELETE;
        }
        
        public boolean isInsert() {
            return this == INSERT;
        }
        
        public static Operation findBy(String operation) {
            for (Operation value : values()) {
                if (value.getOperation().equals(operation)) {
                    return value;
                }
            }
            
            throw new UnsupportedOperationException("해당하는 연산이 없습니다.");
        }
    }

• enum 에 별도 Operation 을 정의

if (operation.isInsert()) {
    doublyProirityQueue.put(num, doublyProirityQueue.getOrDefault(num, 0) + 1);
    continue;
}

• 삽입 연산이다.
• 출현 횟수를 value 로 저장한다.
• 이미 존재하면 출현 횟수 + 1

if (operation.isDelete()) {
    if (doublyProirityQueue.isEmpty()) {
        continue;
    }

• 삭제 연산
  • 큐가 비어있으면 삭제 연산 무시

if (isMinValueOf(num)) {
    int value = doublyProirityQueue.get(doublyProirityQueue.firstKey());
    if (value == 1) {
        doublyProirityQueue.remove(doublyProirityQueue.firstKey());
        continue;
    }
    doublyProirityQueue.put(doublyProirityQueue.firstKey(), value - 1);
    continue;
}

• 최솟값인경우, 출현 횟수가 1이면, 아예 삭제하고 아닌 경우 1을 감소시킨다.
  
• 최댓값 삭제

if (doublyProirityQueue.isEmpty()) {
    sb.append(EMPTY).append("\n");
    continue;
}
sb.append(doublyProirityQueue.lastKey()).append(" ").append(doublyProirityQueue.firstKey()).append("\n");

• 모든 연산 후에 큐가 비어있는 경우 EMPTY 를 출력한다.
• 그렇지 않는 경우 최댓값(lastKey) 와 최소값(firstKey) 을 출력함.

트리 맵에서는 어떻게 firstKey 과 lastKey 가 상수 시간에 접근가능한것 일까?

1. 내부 구조

   1. RB 트리 ( 레드 블랙 트리) … 균형 이진 검색 트리로 트리맵은 구성되어 있다.
   2. 해당 트리트는 항상 균형을 유지한다. ( == O(log n) ) 시간 복잡도를 보장한다.

2. 추가 참조

   1. Treemap 은 내부적으로 가장 작은 키 와 큰 키에 대한 직접적인 참조를 별도로 유지한다.
   2. 트리가 수정될 떄 마다 업데이트됨.

   • 잠깐..

     public K firstKey() {
         return key(getFirstEntry());
     }
     
     // getFirstEntry() 는
     
     final Entry<K,V> getFirstEntry() {
         Entry<K,V> p = root;
         if (p != null)
             while (p.left != null)
                 p = p.left;
         return p;
     }
     
     //left 혹은 right 노드를 타고 들어가면 항상 최소, 최댓값인 키임.
         
     // getLastEntry() 는
     
     final Entry<K,V> getLastEntry() {
         Entry<K,V> p = root;
         if (p != null)
             while (p.right != null)
                 p = p.right;
         return p;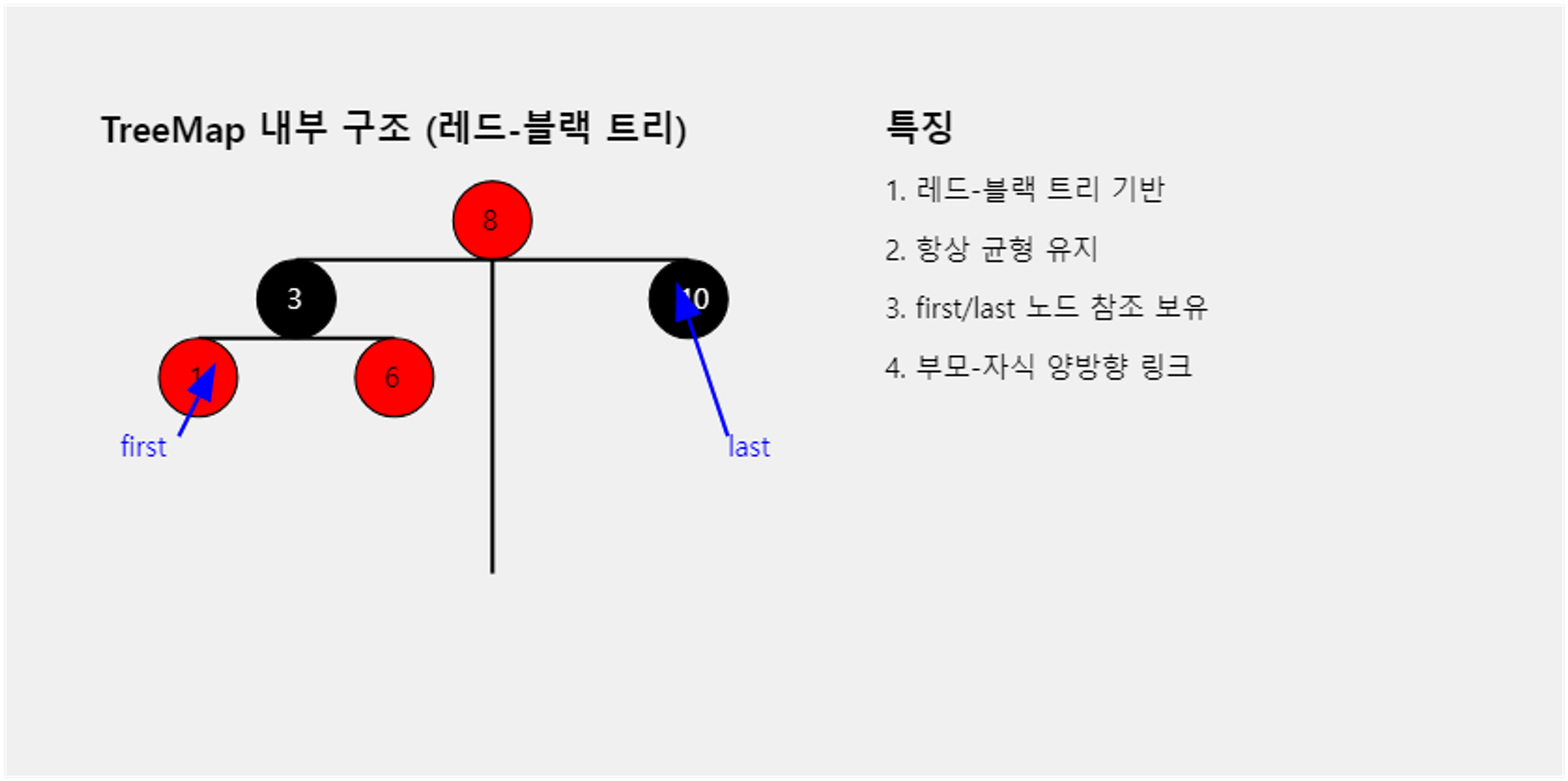
     }

     

     • 가장 작은 값은 항상 트리의 최하단 가장깊은 left, 가장 큰 값은 항상 트리의 가장 깊은 right 이다.