[알고리즘 1058] 친구

개요

1. A 와 B가 직접 친구이거나
2. A 와 B 모두와 친구인 C 가 존재하는 경우

2-친구가 된다고 한다.

알고리즘

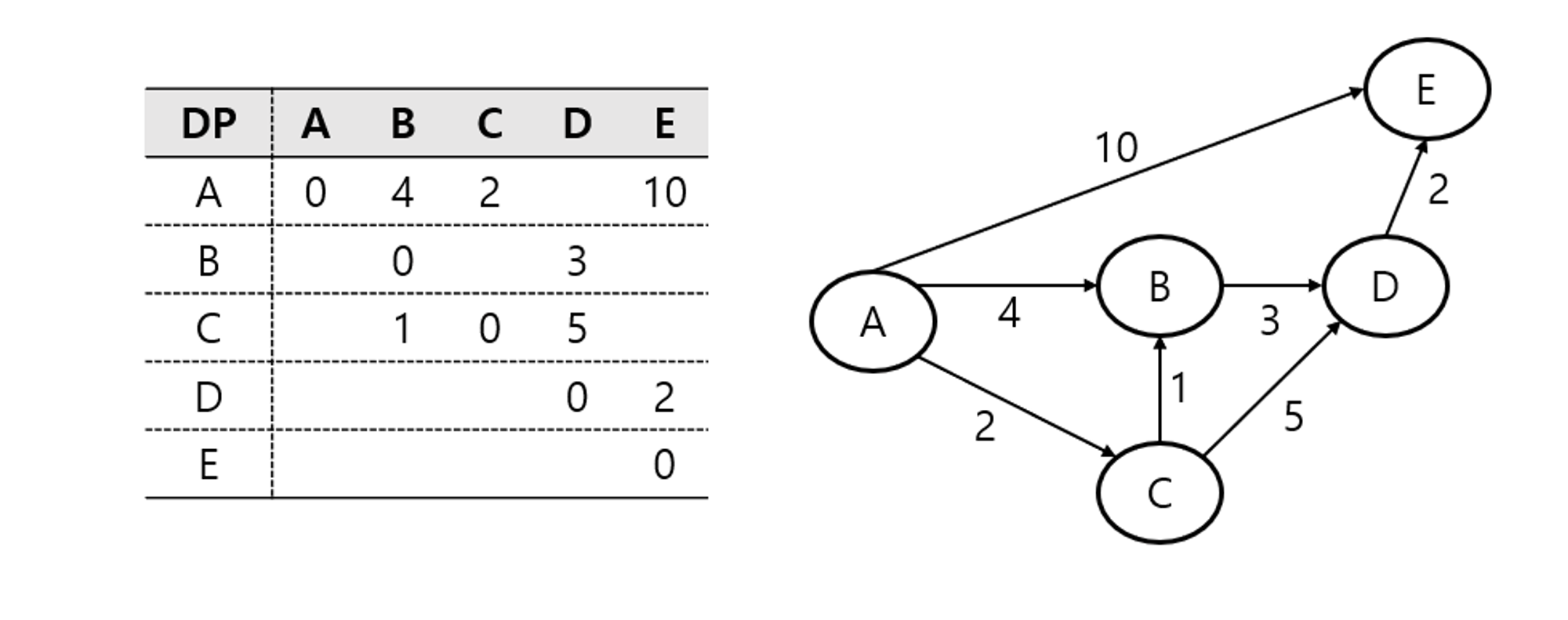
• 플로이드 워셜 알고리즘
  • 그래프에서 모든 장점 쌍 사이의 최단 경로를 찾는 알고리즘이다.
  • 다익스트라, 벨만포드 알고리즘는 한 노드에서 모든 노드까지 최단경로인 반면 플로이드 워셜 알고리즘은
    
  1. 목적
     • 그래프의 모든 정점에서 다른 모든 정점까지의 최단 거리를 계산함.
  2. 방법
     1. 모든 정점 쌍에 대해 반복을 수행한다.
     2. 각 반복에서 새로운 중간 정점을 고려해 경로를 갱신한다.
  3. 시간복잡도
     1. O(V^3)
        1. 중간 노드 K ( 0 ~ N ) , 2차원배열 순회 행 i , 열 j 을 전체 순회함.
  • 알고리즘 상에서는
    • 중간 노드가 서로 모르는 친구를 이어주는 중간 친구가 됩니다.

코드

public static final int DIRECT_FRIEND_VALUE = 1;

// 본인이랑 이어진 경우 0으로 설정
public static final int INDIRECT_FRIEND_VALUE = 0;

// 거리값의 최대가 10,000 이 나오지 않기에 10,000 으로 설정함
public static final int MOCKED_INF_VALUE = 10000;

• 직접 친구 = 1 로 기록
• 본인인 경우 0 으로 기록
• 거리값의 최대가 10,000 이 나오지 않기에 10,000 으로 설정 ( 최단 거리를 구하기에 10,000 을 만나면 최단으로 항상 인지되지 않을거임

// 친구 관계를 그래프로,, 각 친구는 정점이며, 관계는 간선으로 표현한다..
// 직접 친구인 경우 1 , 아닌 경우 0, 친구가 아닌 경우 10,000 으로 설정한다.
for (int i = 0; i < N; i++) {
    String[] st = br.readLine().split("");
    
    for (int j = 0; j < N; j++) {
        if (isMe(i, j)) {
            friends[i][j] = INDIRECT_FRIEND_VALUE;
            continue;
        }
        
        if (isY(st[j])) {
            friends[i][j] = DIRECT_FRIEND_VALUE;
            continue;
        }
        
        if (isN(st[j])) {
            friends[i][j] = MOCKED_INF_VALUE;
        }
    }
}

---

  // 특정 사용자의 친구가 2명 이하인지 확인
  private static boolean isTwoFriends(int j, int[] friends) {
      return friends[j] <= 2;
  }
  
  private static boolean isMe(int i, int j) {
      return i == j;
  }
  
  private static boolean isN(String ny) {
      return Objects.equals(ny, "N");
  }
  
  private static boolean isY(String ny) {
      return Objects.equals(ny, "Y");
  }

1. 2차원 배열의 값중에
   1. 나는 0으로, 직접 친구는 1로, 아무것도 아닌 경우 10000으로 설정

// 플로이드 워셜
for (int k = 0; k < N; k++) {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            //나 인 경우는 패스한다..
            if (isMe(i, j)) {
                continue;
            }
            
            //중간 노드 k , 출발 i , 도착 j -> 중간 노드를 하나씩두고 만약 거쳐간 경우의 최소 거리를 찾는다.
            setShortestCount(friends, i, j, k);
        }
    }
}

• 플로이드 워셜 3중 for 문.

private static void setShortestCount(int[][] friends, int i, int j, int k) {
    // 친구 i -> j  거리값이  = 친구 i -> k + 친구 k -> j 거리값 보다 크다면 친구 i -> j 거리값을 친구 i -> k + 친구 k -> j 거리값으로 설정한다.
    if (friends[i][j] > friends[i][k] + friends[k][j]) {
        friends[i][j] = friends[i][k] + friends[k][j];
    }
}

• 중간 노드를 정해놓고, 가장 최단 거리를 구합니다.
• 나중에 해당 최단 거리는 조건에만 맞는다면 주기적으로 갱신이 되겠죠

// 2- 친구수 계산
int maxFriend = 0;

for (int i = 0; i < N; i++) {
  int friendCount = 0;
  for (int j = 0; j < N; j++) {
      if (isMe(i, j)) {
          continue;
      }
      
      if (isTwoFriends(j, friends[i])) {
          friendCount++;
      }
  }
  
  maxFriend = Math.max(maxFriend, friendCount);
}

• 순회를 돌면서 거리 2 이하의 친구가 각 행마다 몇 명있는지 최대를 갱신합니다.