[자바] 9465 스티커

package org.example.알고리즘.스티커;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {
    public static void main(String[] args) {
        try (BufferedReader br = new BufferedReader(new InputStreamReader(System.in))) {
            int T = Integer.parseInt(br.readLine());
            StringBuilder sb = new StringBuilder();
            
            while (T-- > 0) {
                int n = Integer.parseInt(br.readLine());
                int[][] ns = new int[2][n];
                
                for (int i = 0; i < 2; i++) {
                    String[] input = br.readLine().split(" ");
                    for (int j = 0; j < n; j++) {
                        ns[i][j] = Integer.parseInt(input[j]);
                    }
                }
                
                int[][] dp = new int[3][n];
                
                //윗 스티커 뗀 경우
                dp[0][0] = ns[0][0];
                //아랫 스티커 뗸 경우
                dp[1][0] = ns[1][0];
                //둘다 안뗀 경우
                dp[2][0] = 0;
                
                for (int i = 1; i < n; i++) {
                    //윗 스티커 뗀 경우
                    dp[0][i] = Math.max(dp[2][i - 1], dp[1][i - 1]) + ns[0][i];
                    
                    //아랫 스티커 뗸 경우
                    dp[1][i] = Math.max(dp[2][i - 1], dp[0][i - 1]) + ns[1][i];
                    
                    //아래 스티커도 떼지 않은 경우
                    dp[2][i] = Math.max(dp[0][i - 1], Math.max(dp[1][i - 1], dp[2][i - 1]));
                }
                
                int max = Math.max(dp[0][n - 1], Math.max(dp[1][n - 1], dp[2][n - 1]));
                
                sb.append(max).append("\n");
            }
            
            System.out.println(sb);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
}

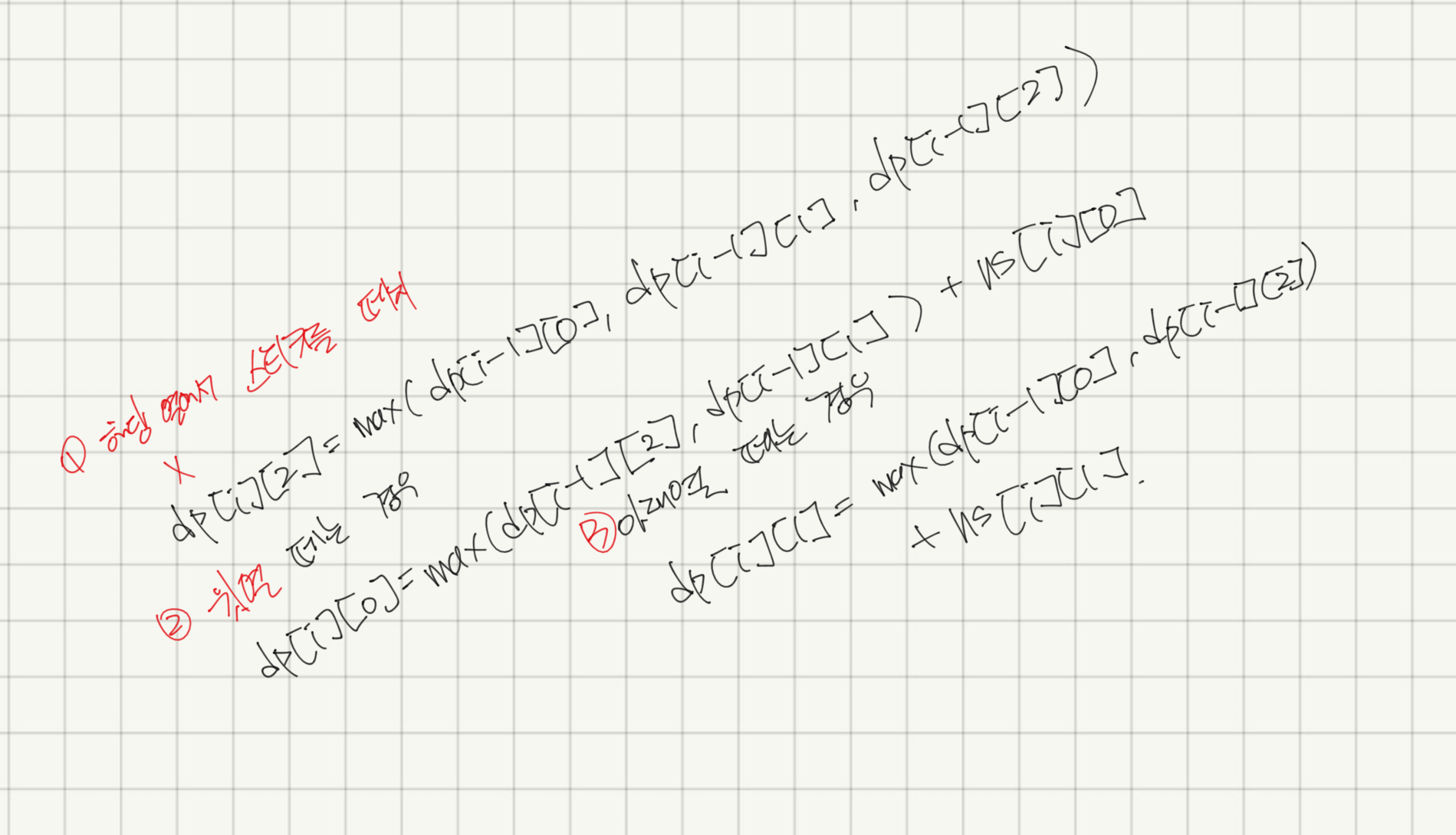
• 그림이 기울어져 있어서 좀 그렇긴한데

  • 해당 열에서 스티커를 떼지 않는 경우

  • 해당 열에 위쪽 스티커를 떼는 경우

  • 해당 열에서 아랫쪽 스티커를 떼는 경우

    로 나눠서 생각하면 된다.

    그게 윗 점화식이 된다.