[ 글의 목적: 컴퓨터가 소수점을 저장하는 방법, 부동소수점과 고정소수점 정리와 python deciaml 예시 정리 ]

소수점 표현

이 현상은 python에만 국한되는 것이 아니라 "IEEE 754 부동소수점 방식" 표준을 따르는 모든 언어에서 공통되게 나타나는 현상이다. 그럼 왜 이런 형상이 나타나는지, 컴퓨터의 소수점 저장방식과 표준에 대해서 살펴보자! (누군가에게는 엄청 지루한 topic일 가능성이 높다🙃)

>>> a = 0.1
>>> b = 0.2
>>> 0.3 == a+b
False
>>> a+b
0.30000000000000004

1. 컴퓨터의 소수점 표현

• 우리가 흔히 사용하는 자료구조 float은 실수이며 소수점은 "부동소수점"으로 표현한다. 여기서 "부동" 이라는 이름 때문에 "움직이지 않는가?.." 라고 생각을 할 수 있다. 하지만 놀랍게 뜰 부(浮)를 사용하며, 소수점의 위치를 고정하지 않는 것을 말한다.

• 컴퓨터는 우리가 선언한 변수(뿐 아니라 실행 중인 정보를)를 어디에 저장하는가? 기본적으로 "주기억 장치 - RAM" 에 저장한다. 흔히 "주기억장치 - 책상", "보조기억장치 - 책장" 으로 비교를 많이 한다. 읽고 싶은 책을 찾기 위해 보조기억 장치에서 찾고, 읽기 위해 책상에 올려둔다. 한 번에 많은 책을 펼치고 싶으면 일단 책상이 넓어야 한다.

• RAM에 대해 너무 깊게 들어가면 전혀 다른 주제가 되니 핵심만 리마인드 해보자! 우리가 선언한 "변수"는 하드웨어적으로 RAM의 memory cell에 저장되며 CPU가 빠르게 접근할 수 있다. 이 메모리 셀은 bit 라는 최소한의 단위로 만들어 졌다.

1) bit

• bit는 RAM이 기억하는 최소한의 단위다. 컴퓨터 하드웨어 탄생들의 시기에는 전기적 신호를 가장 단순하게 표현할 수 있는 진수는 2진수 였다. 예를 들어 전류가 흐를때(ON) 1, 흐르지 않을때(OFF) 0 으로 말이다.

• 그래서 1bit는 0 또는 1밖에 저장하지 않는, "2진수 기억 단위" 라고 생각하면 된다. 그리고 8개가 모여, 8bits = 1byte 가 된다. 그리고 IEEE 754 표준은 부동 소수점을 처리할 때 64bits (8bytes) 를 사용한다. 더 정확하게는 single-precision 은 32bits, double-precision 은 64bits, java에서는 전자를 float, 후자가 double, python에서는 double이 float이다. datatype만으로 bits를 구분하면 헷갈릴 수 있다.

2) bit로 숫자 표현하기

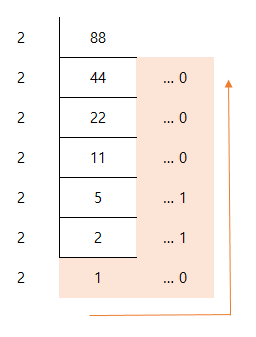
• bit는 2진법이 될 수 밖에 없다. 그러니 우리, 사람이 일반적으로 사용하는 "10진법 체계"를 모두 "2진법 체계"로 바꿀 필요가 있다. 88을 2진수로 표현하려면? 더 이상 나눌 수 없을 때 까지, 2로 계속 나누면 된다. 아래 사진과 같이 계산해, 1011000(2) 가 된다!

• 그러면 소수점의 경우, 실수의 경우는 어떨까? 9.6875 를 위와 같은 방법으로 바꿔보자! 이 경우는 9와 소수부분 0.6875를 따로 계산해야 한다.

• 그림과 같이 소수 부분에 2를 곱해나간다. 만일 2를 곱한 결과가 1을 넘을 경우 1을 빼준다. 각 단계에서 정수 부분(1 or 0)을 2진수로 얻어낸다. 위의 경우 최종 결과가 0.0이 나와서 멈췄지만, 대부분의 실수는 무한히 순환하며 반복된다. 그렇기 때문에 "적당한 개수의 유효숫자만을 취하게 된다. 이 과정에서 먼저 오차가 발생하게 된다." 결국 9.6875를 2진법으로 표현하면 1001.1011(2) 이 됨을 알 수 있다.

• 아니 그래서, 이게 도대체 왜 문제가 생기는 걸까? 일단 이렇게 2진화된 숫자를 진짜 컴퓨터는 어떻게 저장할까? 그리고 그 표준이라는 친구는 어떻게 저장하는 걸 표준이라고 한걸까?

3) float, IEEE 754 표준

• 일단 표준에서 핵심을 살펴보자. 표준에서는 float을 저장하고 처리하기 위해 64bits를 사용한다고 언급했다. 그 표준의 가장 핵심은 아래 사진과 같다.

• 참고로 더 정확하게 32bits를 사용할 수 있다. single-precision (32-bit) binary floating-point format, double-precision (64-bit) binary floating-point format 로 나뉜다. single의 경우 부호부 1Bit | 지수부 8Bit | 가수부 23Bit

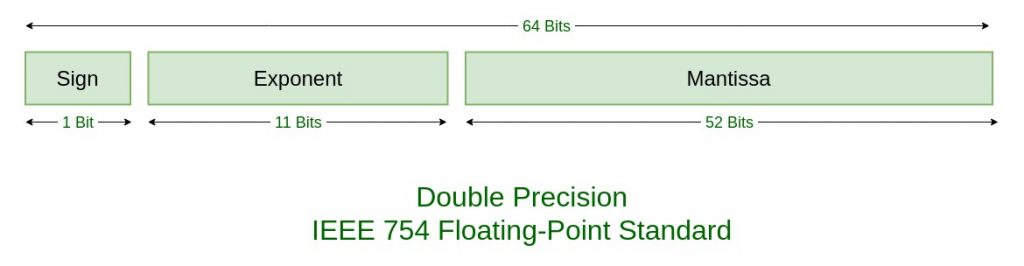
1. Sign은 부호부분으로써 양수(0) 인지 음수(1) 인지를 나타내고 1비트를 사용한다.
2. Exponent는 지수부분 으로써 11비트를 차지한다.
3. Mantissa(또는 Fraction)는 가수부분 으로써 52비트를 차지한다.
4. 총 64비트로 이루어져 있다.

(1) Exponent - 지수부분

• 위에든 예시로 1001.1011(2)는 "그대로 저장하면 고정 소수점" 이 된다. 정수부, 소수부를 그냥 각각 저장한다고 생각하면 된다. (자세한 설명은 아래에서 다시 언급할 예정이다.)

• 다른 예시를 생각해 보자, 0.1 10진수를 2진수로 표현하면 어떤 값이 나올까? 위에 든 예시와 달리 0.0001100110011001100110011001100110011001100110011... 와 같이 무한히 0과 1이 나온다!

• 자 그럼 여기서, 일단 적당히 짤라서, 2진수값 소수점을 기준으로 왼쪽에 1이 될 때까지 끌어다 온다. 1.10011001100110011001101, 총 4칸을 옮겼다. 즉 이 행위를 "지수로" 표현하면 2^-4 와 같다. 그래서 1.10011001100110011001101 x 2^(-4) 로 표현할 수 있다.

• 여기서 Exponent 개념을 좀 더 살펴보자. 1이 11개인 2진수는 11111111111(2), 2047(10)이 된다. 하지만 이 11비트로 exponent값 자체가 음수인지 양수인지 판단해야한다. 그때 "bias 값" 이라는 것을 사용한다. 우리가 exponent을 저장할 때 실제로는 bias값과 exponent의 합을 저장하게 된다. bias더하면 실제의 음수를 저장하지 않고서도 음수라는 것을 표현할 수 있다.

• 그리고 64bis(double)에서는 이 bias가 1023이 된다.. 그래서 2047 (the largest biased exponent) - 1023 (the bias value) = 1024 값이 나오고, 0 (the smallest biased exponent) - 1023 (the bias value) = -1023 이 되면서 -1022 to +1023 범위 값을 11bits exponent field 에 사용해야 한다. 이런 표기법이 "바이어스 표현법"이다.

• 쉽게 (2^(Exponent bit - 1) ) + 1 + (소수점 몇번 움직였냐) 의 계산식으로, (2^10) + 1 - 4 가 되며, 1019 라는 숫자를 얻을 수 있다. 이는 2진법으로 1111111011를 의미하며, 10자리라 맨 앞에 0을 붙여 01111111011를 얻을 수 있다.

(2) Mantissa - 가수부분

• 위에서 1.10011001100110011001101..., 총 4칸을 옮겼다. 그리고 오른쪽 부분 전체가 "가수 부분" 이 된다. 총 52자리를 써야하니 짤린 부분을 그대로 가지고 오면 된다. 1001100110011001100110011001100110011001100110011010 가 된다.

(3) 0.1 의 float 실제 저장 형태 - 2진수

• 부호부분: 0

• 지수부분: 01111111011

• 가수부분: 1001100110011001100110011001100110011001100110011010

• 최종 표기: 0 01111111011 1001100110011001100110011001100110011001100110011010(2)

• 실제 컴퓨터는 최종표기와 같은 2진수 형태로 부동소수점 값을 저장한다. https://www.h-schmidt.net/FloatConverter/IEEE754.html 에서 실제 변환값, 저장값, 오차범위를 확인할 수 있다.

2. 부동소수점과 고정소수점 정리

1) 부동소수점

• 위에서 IEEE 754 double precision 2진수 표기법을 보면서 float에 대해 조금 더 자세하게 알아봤다.

• 그럼 오차범위 가능성이 있는 부동소수점을 왜 쓰는 것일까? 정확하게 지수가 커지면 커질수록 오차 또한 급격하게 커질 수 밖에 없다. 하지만 "엄청나게 작은 수를 표현할 수 있다."

• 우리가 나이를 어떻게 세는가? 몇 살이냐고 물어보면, "태어난지 10137일 정도 지난 것 같아요" 라고 하지 않는다. 광년은 어떤가? 10억 광년이 진짜 10억 ..... 0.231312 광년 이 중요한가? 그래서 부동소수점을 쓴다. 고정소수점으로 접근할 수 없는 자리수 그 이상을 러프하게 계산할 수 있으니, 우주 계산에는 부동소수점이 아직까지는 좋은 접근법이다.

2) 고정소수점

• 고정소수점은 부동소수점에 비해 계산하기 편하다. 소수점 자리수를 정해두고 그냥 있는 그대로 2진수화 하면 끝이다.

• 쉽게 32bits 예시부터 보면 [ 0 000000000000000 0000000000000000 ] 순서로, 부호, 정수, 소수점 이하 자릿수라고 해보자. 9.6875 을 계산해보자.

• 정수는 9이므로 [ 000000000001001 ], 소수점 이하는 6875이므로 [ 1011000000000000 ] (어떻게 되었냐는 위 "bit로 숫자 표현하기" 계산하는 식을 참조!), 즉 [ 0 000000000001001 1011000000000000 ] 이 된다. 64bits는 표현할 수 있는 범위만 넓어지니 생략하겠다.

• 이런 고정소수점은 "표현할 수 있는 범위가 부동소수점에 비해 매우 적다"는 단점이 존재한다. 하지만 부동소수점에서 오차가 엄청 중요한 경우, 즉 "돈을 다루는 값" 같은 경우는 "고정소수점"을 사용하는게 올바른 접근이다. 게다가 돈은 소수점 아래를 그렇게 많이 사용하지 않고, [ 뱅커스 라운딩 (오사오입 반올림) - 올려질 값이 5인 경우에 만들어질 수의 끝이 짝수가 되도록(짝수에 수렴) 하는 방식 ] 을 채택하기 때문에 이 "고정소수점"에 딱 맞다.

3) python에서 고정소수점

다시 처음으로 돌아가, Python에서 0.1 + 0.2 = 0.30000000000000004 라고 해버린다. 위에서 살펴본 IEEE 754 double precision 에 의해 0.3의 근삿값이 나오는 것이다.

(1) Decimal

• 고정소수점을 사용하려면 python 내장 decimal 모듈의 Decimal datatype을 활용하면 된다. Decimal('0.1') + Decimal('0.2') = Decimal('0.3') 이 나온다.

>>> from decimal import Decimal
>>> Decimal('0.1') + Decimal('0.2')
Decimal('0.3')

• 참고로 python의 round는 "특이하다" 라는 얘기를 들어봤을 것이다. 올려질 자리수를 "짝수로 만들게끔" 올림하기 때문이다. 근데 decimal은 "반올림 하는 방법을 정할 수 있다". decimal의 ROUND_HALF_UP, ROUND_HALF_DOWN, ROUND_UP 등이 있다.

from decimal import Decimal, ROUND_HALF_UP

# Define a Decimal object for a currency value
value = Decimal('25.945')

# Round the value to two decimal places
rounded_value = value.quantize(Decimal('.01'), rounding=ROUND_HALF_UP)

print(rounded_value)  # Output: 25.95

• quantize 라는 Decimal method는 반올림 방법과 자리수를 정해 아주 정확하게 예상한대로만 반올림이 되게끔 하는데 도움을 주는 친구이다. 돈 계산에 이 보다 나은 방법이 있을까 싶다.

• 즉 위 deciaml object "25.945"를 quantize(올려질 자리수, 라운딩 방법) method 으로 2번째 자리에서 "round to the nearest value with ties going towards zero" 방법으로 반올림 했다.

value = Decimal('10.12512439')
rounded_value = value.quantize(Decimal('.01'), rounding=ROUND_HALF_UP)
print(rounded_value)  # Output: 10.13

value = Decimal('10.12512439')
rounded_value = value.quantize(Decimal('.0001'), rounding=ROUND_HALF_UP)
print(rounded_value)  # Output: 10.1251

(2) django model도 DecimalField 이 있다.

• 해당 model field에 대한 소개는 Django Model - 필드(filed) 모음집로 대체한다.

출처

• chatGPT
• https://irem.univ-reunion.fr/IMG/pdf/ieee-754-2008.pdf
• IEEE 754는 Willan Khan으로 부터 출발했다. 인터뷰 보기
• https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
• https://betterprogramming.pub/why-is-0-1-0-2-not-equal-to-0-3-in-most-programming-languages-99432310d476
• https://0.30000000000000004.com/
• https://readyfortest.tistory.com/47
• https://www.h-schmidt.net/FloatConverter/IEEE754.html