이번 시간엔 우선순위큐에 대해서 알아보겠다.
우선순위큐란?
큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형식의 자료구조이다.
우선순위 큐(Priority Queue)는 먼저 들어오는 데이터가 아니라, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조이다.
우선순위 큐는 일반적으로 힙(Heap)을 이용하여 구현한다.
힙이란?
힙(Heap)은 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조이다.
여러 개의 값 중 최댓값 또는 최솟값을 찾아내는 연산이 빠르다.
힙의 특징
완전이진트리 형태로 이루어져 있다.
부모노드와 서브트리간 대소 관계가 성립된다. (반정렬 상태)
이진탐색트리(BST)와 달리 중복된 값이 허용된다.
힙의종류
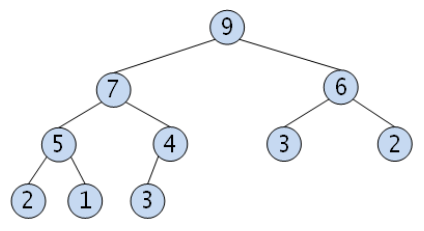
최대 힙 (Max Heap)
부모 노드의 키 값이 자식 노드보다 크거나 같은 완전이진트리이다.
❝ key(부모노드) ≥ key(자식노드) ❞
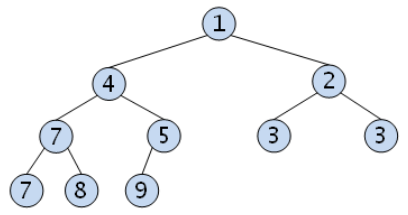
최소 힙 (Min Heap)
부모 노드의 키 값이 자식 노드보다 작거나 같은 완전이진트리이다.
❝ key(부모노드) <= key(자식노드) ❞
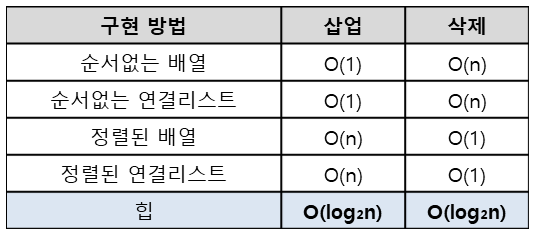
우선순위 큐를 힙이 아니라 배열 또는 연결리스트를 이용하여 구현할 수도 있다.
하지만 배열과 연결리스트는 선형 구조의 자료구조이므로 삽입 또는 삭제 연산을 위한 시간복잡도는 O(n)이다.
반면 힙트리는 완전이진트리 구조이므로 힙트리의 높이는 log₂(n+1)이며, 힙의 시간복잡도는 O(log₂n)이다.
우선순위 큐 구현
1. 힙 구현
힙은 일반적으로 배열을 이용하여 구현한다.
완전 이진트리이므로 중간에 비어있는 요소가 없기 때문이다.
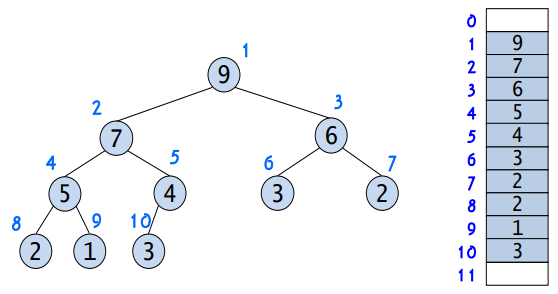
위 그림과 같이 트리의 각 노드에 번호를 붙이고, 이 번호를 배열의 인덱스로 생각하면 효과적으로 힙을 구현할 수 있다.
배열로 구현하였기 때문에 부모 또는 자식 노드를 찾아가는 연산을 구현하기도 간편하다.
자식노드를 구하고 싶을 때
왼쪽 자식노드 index = (부모 노드 index) * 2
오른쪽 자식노드 index = (부모 노드 index) * 2 + 1
부모노드를 구하고 싶을 때
부모 노드 index = (자식노드 index) / 2
2. 삽입연산
힙에 삽입을 하기 위해서는 힙 트리의 성질을 만족시키면서 새로운 요소를 추가해야 한다.
삽입 방법
우선 완전이진트리의 마지막 노드에 이어서 새로운 노드를 추가한다.
추가된 새로운 노드를 부모의 노드와 비교하여 교환한다.
정상적인 힙트리가 될 때 까지 (더이상 부모노드와 교환할 필요가 없을 때까지) 2번을 반복한다.
최악의 경우 새로 추가된 노드가 루트노트까지 비교하며 올라가야 하므로 시간복잡도가 O(log₂n)이다.
2.3 삭제 연산
힙 트리에서 루트노드가 가장 우선순위가 높으므로 루트 노드를 삭제해야 한다.
삭제가 이뤄진 후 힙 트리의 성질이 유지돼야 하므로 아래와 같은 방법으로 삭제를 진행한다.
삭제 방법
-
루트 노드를 삭제한다.
-
루트 노드가 삭제된 빈자리에 완전이진트리의 마지막 노드를 가져온다.
-
루트 자리에 위치한 새로운 노드를 자식 노드와 비교하여 교환한다.
-
이때 최대 힙인 경우 자식노드 중 더 큰 값과 교환을 하며, 최소 힙인 경우 더 작은 값과 교환을 한다.
정상적인 힙트리가 될 때까지 (더 이상 자식노드와 교환할 필요가 없을 때까지) 3번을 반복한다.
삭제 연산 또한 최악의 경우 루트노트부터 가장 아래까지 내려가야 하므로 시간복잡도가 O(log₂n)이다.
힙 구조체 선언
typedef struct{
int heap[MAX_ELEMENT];
int heap_size;
}HeapType;
삽입 연산 구현
void insertHeap(HeapType* h, int item)
{
int i;
h->heap_size = h->heap_size + 1;
i = h->heap_size;
while ((i != 1) && (item > h->heap[i / 2]))
{
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item;
}
//삽입 같은 경우는 큰 개념은 이와같다.
// 1. 히프의 크기를 하나 증가시켜서 노드 위치를 확장하고 확장한 노드 번호가 현재의 삽입 위치 i가 된다.
// 2. 삽입할 원소 item과 부모노드 heap[i/2]를 비교하여 item이 부모 노드보다 작거나 같으면 현재의 삽입 위치 i를 삽입 원소의 위치로 확정한다.
// 3. 만약 삽입할 원소 item이 부모 노드보다 크면, 부모 노드와 자식 노드의 자리를 바꾸어 최대 히프의 관계를 만들어야 하므로 부모 노드 heap[i/2]를 현재의 삽입 위치 heap[i]에 저장한다.
// 4. i/2를 삽입 위치 i로 하고 2~4를 반복하면서 item을 삽입할 위치를 찾는다.
// 5. 찾은 위치에서 삽입할 노드 item을 저장하면 최대 히프의 재구성 작업이 완성되므로 삽입 연산을 종료한다. 삭제연산
int deleteHeap(HeapType* h)
{
int parent, child;
int item, temp;
item = h->heap[1];
temp = h->heap[h->heap_size];
h->heap_size = h->heap_size - 1;
parent = 1;
child = 2;
while (child <= h->heap_size)
{
if ((child < h->heap_size) && (h->heap[child]) < h->heap[child + 1])
child++;
if (temp >= h->heap[child]) break;
h->heap[parent] = h->heap[child];
parent = child;
child = child * 2;
}
h->heap[parent] = temp;
return item;
//1,루트 노드 heap[1]을 itemp 에 저장하고.
//2. 마지막 노드의 원소 heap[h->heap_size]를 temp에 임시 저장한 후에
//3. 전체 노드의 개수가 줄어든 히프가 되도록 하기 위하여 노드의 개수를 1 감소시킨다.
//4. 마지막 노드의 원소였던 temp의 임시 저장 위치 parent는 루트 노드 자리인 1번이 된다.
//5. 현재 저장 위치에서 자식 노드 heap[child]와 heap[child + 1]이 있을 때, 둘 중에서 키값이 큰 자식 노드의 키값과 temp를 비교하여 temp가 크거나 같으면 현재 위치가 temp의 자리로 확정된다.
//6. 만약 temp가 자식 노드보다 작으면 자식 노드와 자리를 바꾸고 다시 5~6을 반복하면서 temp의 자리를 찾는다.
//7. 찾은 위치에 temp를 저장하여 최대힙 잭성 작업을 완료시키고 루트 노드를 저장한 item을 반환하는 것으로 삭제 연산을 종료한다.
}