Today I Learned

매일 배운 것을 정리하며 기록합니다. Time Complexity를 공부하였습니다.

---

Time Complexity(시간 복잡도)

• 알고리즘을 해결하는데 걸리는 시간과 입력의 함수 관계를 가르킴
• 즉, 연산의 횟수

---

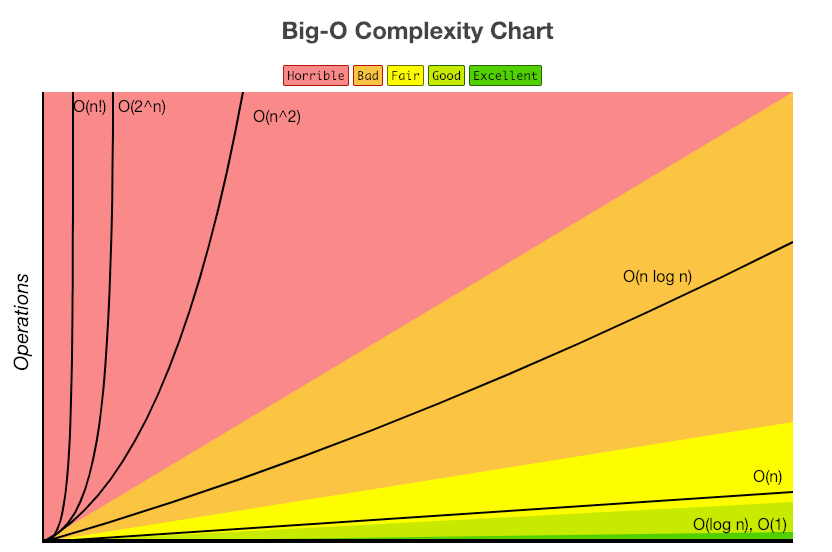
Big O natation(빅오 표기법)

• 알고리즘의 효율성을 수학적으로 표기해주는 표기법
• 계수법칙으로 인해 계수와 상수는 제거함
• 알고리즘의 시간과 공간 복잡도를 표현할 수 있음
• 입력 데이터가 주어졌을 때 덧셈, 뺄셈, 곱셈 같은 기본 연산의 횟수를 의미
• 알고리즘 효율성을 상한선 기준으로 표기, Worst Case (알고리즘 효율성은 값이 클수록 비효율)
• 알고리즘이 복잡해 질수록 평균적인 경우는 구하기 어려워지기 때문에 최악의 경우로 알고리즘의 성능을 파악

---

O(1)

• Constant time
• 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
• ex) push, pop

---

O(log n)

• 연산이 한 번씩 처리될 때마다 검색해야 하는 데이터의 양이 절반씩 줄어드는 알고리즘
• ex) binary search

---

O(n)

• Linear time
• 입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘
• ex) for문

---

O(n log n)

• ex) 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort)

---

O(n²)

• Quadratic time
• 똑같은 O(n)의 연산이 2개 있을 때
• ex) 2중 for문, 삽입 정렬(insertion sort), 버블 정렬(bubble sort), 선택 정렬(selection sort)

---

O(nm)

• Quadratic time
• 다른 O(n)의 연산이 2개 있을 때

---

O(n³)

• Polynomial/Cubic time
• 똑같은 O(n)의 연산이 3개 있을 때

---

O(2ⁿ)

• Exponential time
• ex) 피보나치 수열

---