[프로그래머스_ Java_Lv0] 순서쌍, IntStream

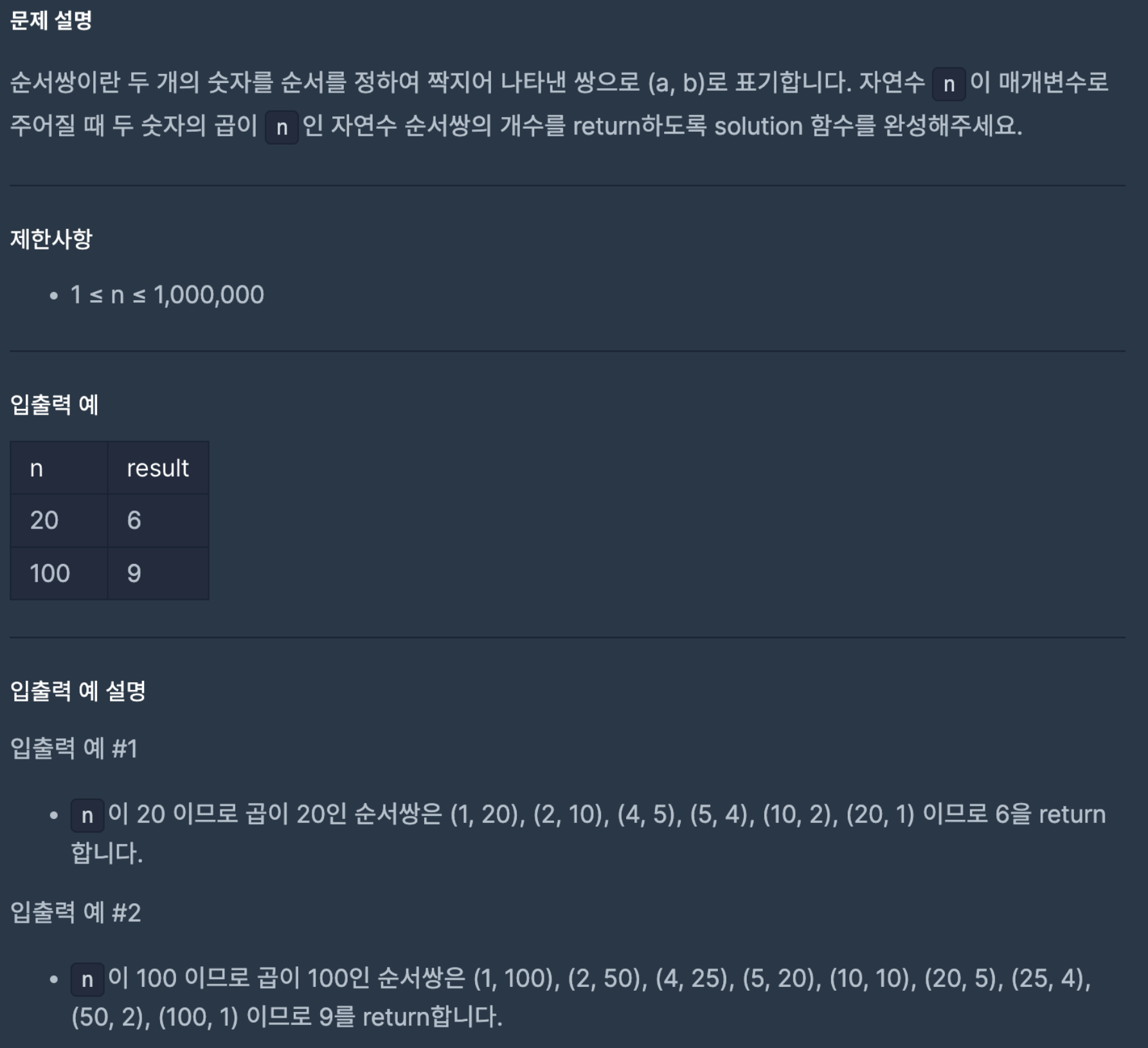
class Solution {
    public int solution(int n) {
        int count = 0;
        
        for(int i = 1; i * i <= n; i++) { // √n 까지만 반복
            if (n % i == 0) {
                count += (i == n / i) ? 1 :2; // 중복 방지
            }
        }
        return count;
    }
}

✔ 핵심 아이디어

• (a, b)가 n의 약수라면 (b, a)도 성립한다.

• 즉, 약수의 개수 × 2를 반환하면 된다.

• 약수를 찾을 때 1부터 n까지 다 검사하면 비효율적이다.

• √n까지만 탐색하면 빠르게 해결 가능하다.

✔ 풀이

1️⃣ 1부터 √n까지만 탐색 (i * i <= n)

• i가 n의 약수이면 (i, n/i)와 (n/i, i) 두 개의 순서쌍이 존재.

2️⃣ (i == n / i)이면 (4, 4)처럼 중복이므로 +1

• 일반적인 경우 두 개의 순서쌍이 있으므로 +2

---

다른사람 풀이

class Solution {
    public int solution(int n) {
        return (int) IntStream.rangeClosed(1, n).filter(i -> n % i == 0).count();
    }
}

1️⃣ IntStream.rangeClosed(1, n)

• 1부터 n까지의 숫자를 순차적으로 생성하는 스트림을 만든다.
• 즉, 1부터 n까지 모든 숫자를 반복하며 확인하는 역할.

2️⃣ .filter(i -> n % i == 0)

• i가 n의 약수인지 확인하는 과정
• n % i == 0이면 i는 n의 약수이므로 스트림에 남김
• 그렇지 않으면 제외됨.

3️⃣ .count()

• 약수의 개수를 세서 반환
• count()는 long 타입을 반환하므로 (int)로 변환 필요하다.

✅ 약수(순서쌍) 개수 구하기

• (a, b)가 n의 약수 쌍이면 (b, a)도 항상 존재.
• 하지만 IntStream.rangeClosed(1, n) 방식에서는 중복 없이 한 번만 계산된다.
  👉 이미 약수 개수 자체가 곧 정답이 된다!