문제

Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

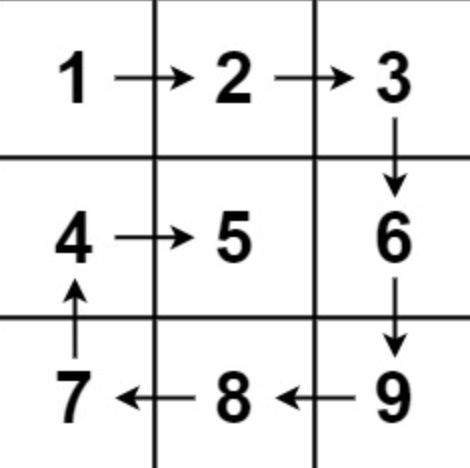
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
Example 2:

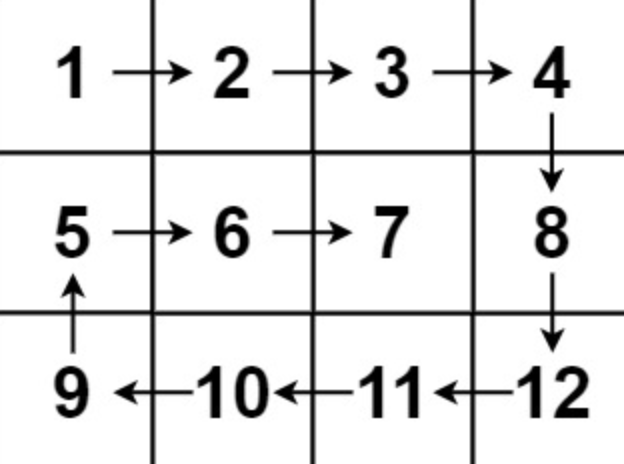
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

작성한 코드

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    const xLen = matrix[0].length;
    const yLen = matrix.length
    const output = [];

    const initMatrix = matrix.map((innerMatrix) => innerMatrix.map((val) => val = 0));
    const finalX = Math.floor(xLen / 2);
    const finalY = Math.floor(yLen / 2); 

    // 초기 행렬 생성

    let currX = 0;
    let currY = 0;
    let currDir = {
        x: 1,
        y: 0
    }
    for (i = 0; i < xLen * yLen ; i++) {
        if (isValid(currX + currDir.x, currY + currDir.y, xLen, yLen)) 
        isVisited = initMatrix[currY + currDir.y][currX + currDir.x];
        if ( isVisited || !isValid(currX + currDir.x, currY + currDir.y, xLen, yLen)) {
            currDir = changeDir(currDir);
        }

        output.push(matrix[currY][currX]);
        initMatrix[currY][currX] = 1;
        
        currX += currDir.x;
        currY += currDir.y;
    }
    return output
};

function changeDir (currDir) {
    // x 방향 이동
    if (currDir.x === 1 && currDir.y === 0) return { x: 0, y: 1};
    // -y 방향 이동
    if (currDir.x === 0 && currDir.y === 1) return { x: -1, y: 0};
    // -x 방향 이동
    if (currDir.x === -1 && currDir.y === 0) return { x: 0, y: -1};
    // y 방향 이동
    if (currDir.x === 0 && currDir.y === -1) return { x: 1, y: 0};
}

function isValid (newX, newY, xLen, yLen) {
    if (newX > xLen - 1) return false;
    if (newY > yLen - 1) return false;
    if (newX < 0) return false;
    if (newY < 0) return false;
    return true;
}

아이디어

n X m 행렬을 나선방향으로 돌며 출력을 해야 한다. 그때 n X m 행렬의 바깥으로 빠져나가서는 안되고 이미 방문한 곳을 다시 방문해서는 안된다.

그래서 방문했었는지 여부를 알기 위해 0 으로 채워진 같은 크기의 n X m 행렬 initMatrix 을 생성해주고 현 좌표 (currX, currY) 에서 현재 방향 currDir 만큼 이동했을때 (currX + currDir.x, currY + currDir.y) 방문했었는지 여부와 그렇게 이동했을 때의 좌표가 n X m 행렬 내에 있는지를 보고

현재의 방향을 유지할때의 다음 좌표가 방문했거나 유효하지 않을 경우 방향을 전환 changeDir 하도록 하여 최종 지점까지 반복하도록 하는 구현 코드를 구상했다.

학습

이미 방문한 곳을 다시 방문하면 안된다고 생각했다. 또한 범위 바깥으로 나가는 경우도 고려해야 했고 시간복잡도를 고려하여 O(n^2) 가 발생하는 반복문 내의 반복문이 들어가는 경우를 최대한 피하려 했다. (그래도 초기 initMatrix 를 만드는데 O(n^2) 가 소요된 것 같다.. )

방향을 currDir 라는 객체에 x, y 값으로만 넣어줬는데 차라리 배열과 인덱스 값을 만들어서 const dirArray = [{0, 1}, {1, 0}, {0, -1}, {-1, 0}] 와 dirIndex = 0 을 생성해두고 (dirIndex + 1) % 4 를 하는게 더 깔끔해 보인다.

그럼에도 성능향상과 관련이 있을지에 대해서는 의문이다.

차라리 initMatrix 를 만드는데 O(n^2) 가 소요되는데 이 부분이 더 개선되어야 하지 않을까 싶었다.

// 기존 코드
const initMatrix = matrix.map((innerMatrix) => innerMatrix.map((val) => val = 0));

// 수정한 코드
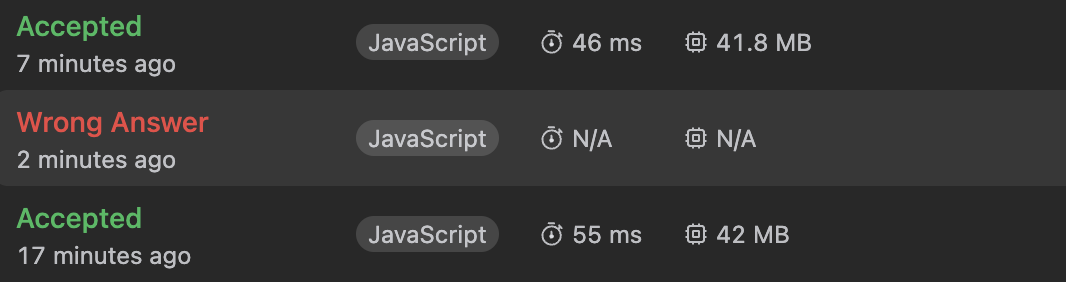
const initMatrix = Array(yLen).fill(false).map(() => Array(xLen).fill(false));

확실히 이부분을 개선하니 성능이 확 좋아졌다.

새로 알게된 사항

Array() constructor

Array 도 생성자함수가 있어서 인자로 number 를 전달하면 주어진 크기만큼의 배열이 생성된다.

Array.prototype.fill()

Array 의 fill() 메서드는 Array 를 특정 범위 혹은 전체를 원하는 값으로 채워줄 수 있다.

const array1 = [1, 2, 3, 4];

// Fill with 0 from position 2 until position 4
console.log(array1.fill(0, 2, 4));
// Expected output: Array [1, 2, 0, 0]

// Fill with 5 from position 1
console.log(array1.fill(5, 1));
// Expected output: Array [1, 5, 5, 5]

console.log(array1.fill(6));
// Expected output: Array [6, 6, 6, 6]

이 둘을 조합하면 Array(yLen).fill(0).map(() => Array(xLen).fill(0)) 를 통해 O(n^2) 에서 O(n) 으로 줄여줄 수 있게 된다.

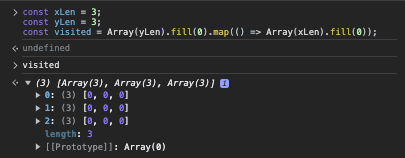
그러나 fill() 이 Array 내부적으로 어떻게 동작하길래 map 을 중첩해서 사용하는 것보다 더 수월했을까?

// 기존 코드
const initMatrix = matrix.map((innerMatrix) => innerMatrix.map((val) => val = 0));

// 수정한 코드
const initMatrix = Array(yLen).fill(false).map(() => Array(xLen).fill(false));

기존코드에서 innerMatrix.map((val) => val = 0) 이 부분을 보면 사실 기존의 값을 가져와서 새로 변한 값을 할당하는 2단계의 동작이 이루어진다. 즉, 기존 값을 복사하고 할당하는 동작이 이루어지는데

수정한 코드에선 크기만 갖는 빈 배열을 만들어두고 값 할당만 이루어져서 메모리 및 성능 측면에서 더 나은 퍼포먼스를 보여주는 것 같다.

애초에 fill 을 통해 전체 행렬을 특정 값으로 채우는 방법을 mdn 에서 소개해주고 있다.