백준_11399_ATM, 백준_1931_회의실배정, 백준_1449_수리공항승

그리디 알고리즘이란?

어떤 문제가 있을 때 단순 무식하게, 탐욕적으로 문제를 푸는 알고리즘을 말한다. 이때 그리디, 탐욕이란 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 말한다. 매 순간 가장 좋아 보이는 것을 선택하며, 현재의 선택이 나중에 미칠 영향에 대해 고려하지 않는다.

보통 그리디 알고리즘은 기준에 따라 가장 좋은 것을 선택하는 알고리즘이라 '가장 큰 순서대로', '가장 작은 순서대로' 같은 기준을 제시해준다. 그러니 정렬 알고리즘과 같이 짝을 지어 출제된다.

예시

거스름돈 문제

500원, 100원, 50원, 10원짜리 동전이 무한히 존재할때 손님에게 거슬러줘야 할 돈이 N 원일 때 거슬러 줘야 할 동전의 최소 개수는? 단, N 은 항상 10의 배수이다.

기준

가장 큰 화폐 단위 부터 돈을 거슬러 주는 것

풀이

n = 1260
count = 0

coin_types = [500, 100, 50, 10]

for coin in coin_types:
	count += n // coin
    n % coin
    
print(count)

문제 출처 : 이것이 취업을 위한 코딩 테스트다 with 파이썬

백준 11399 ATM

문제

인하은행에는 ATM이 1대밖에 없다. 지금 이 ATM앞에 N명의 사람들이 줄을 서있다. 사람은 1번부터 N번까지 번호가 매겨져 있으며, i번 사람이 돈을 인출하는데 걸리는 시간은 Pi분이다.

사람들이 줄을 서는 순서에 따라서, 돈을 인출하는데 필요한 시간의 합이 달라지게 된다. 예를 들어, 총 5명이 있고, P1 = 3, P2 = 1, P3 = 4, P4 = 3, P5 = 2 인 경우를 생각해보자. [1, 2, 3, 4, 5] 순서로 줄을 선다면, 1번 사람은 3분만에 돈을 뽑을 수 있다. 2번 사람은 1번 사람이 돈을 뽑을 때 까지 기다려야 하기 때문에, 3+1 = 4분이 걸리게 된다. 3번 사람은 1번, 2번 사람이 돈을 뽑을 때까지 기다려야 하기 때문에, 총 3+1+4 = 8분이 필요하게 된다. 4번 사람은 3+1+4+3 = 11분, 5번 사람은 3+1+4+3+2 = 13분이 걸리게 된다. 이 경우에 각 사람이 돈을 인출하는데 필요한 시간의 합은 3+4+8+11+13 = 39분이 된다.

줄을 [2, 5, 1, 4, 3] 순서로 줄을 서면, 2번 사람은 1분만에, 5번 사람은 1+2 = 3분, 1번 사람은 1+2+3 = 6분, 4번 사람은 1+2+3+3 = 9분, 3번 사람은 1+2+3+3+4 = 13분이 걸리게 된다. 각 사람이 돈을 인출하는데 필요한 시간의 합은 1+3+6+9+13 = 32분이다. 이 방법보다 더 필요한 시간의 합을 최소로 만들 수는 없다.

줄을 서 있는 사람의 수 N과 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어졌을 때, 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 사람의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어진다. (1 ≤ Pi ≤ 1,000)

출력

첫째 줄에 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 출력한다.

기준

각 손님의 대기 시간의 총합을 최대한 줄이는 것

=> 인출 시간이 적은 순으로 정렬한다.

풀이

N = int(input()) # 사람의 수 1 ~ 1000
P = [int(x) for x in input().split()] # 인출하는데 걸리는 시간 1 ~ 1000

# i 번째 사람이 돈을 인출하는데 걸리는 시간 Pi

P.sort()
sum = 0

for i in range(0, N):
  sum += P[i] * ( N - i )

print(sum)

백준 1931 회의실배정

문제

한 개의 회의실이 있는데 이를 사용하고자 하는 N개의 회의에 대하여 회의실 사용표를 만들려고 한다. 각 회의 I에 대해 시작시간과 끝나는 시간이 주어져 있고, 각 회의가 겹치지 않게 하면서 회의실을 사용할 수 있는 회의의 최대 개수를 찾아보자. 단, 회의는 한번 시작하면 중간에 중단될 수 없으며 한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다. 회의의 시작시간과 끝나는 시간이 같을 수도 있다. 이 경우에는 시작하자마자 끝나는 것으로 생각하면 된다.

입력

첫째 줄에 회의의 수 N(1 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N+1 줄까지 각 회의의 정보가 주어지는데 이것은 공백을 사이에 두고 회의의 시작시간과 끝나는 시간이 주어진다. 시작 시간과 끝나는 시간은 231-1보다 작거나 같은 자연수 또는 0이다.

출력

첫째 줄에 최대 사용할 수 있는 회의의 최대 개수를 출력한다.

기준

빨리 끝나는 회의 순서대로 정렬, 빨리 시작하는 회의 순서대로 정렬

이 문제는 기준이 2개이다. 이 조건을 보자 단, 회의는 한번 시작하면 중간에 중단될 수 없으며 한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다. 빨리 끝나는 회의 순서대로 정렬하면 뒤에서 고려해볼 회의가 많아지고, 이후 빨리 시작하는 회의 순서대로 정렬한다면 회의가 끝나는 것과 동시에 다음 회의가 시작되는 경우를 고려할 수 있다.

풀이

import sys

N = int(sys.stdin.readline().rstrip())
time = []

for i in range(N):
  start, end = map(int, sys.stdin.readline().rstrip().split())
  time.append([start, end])

time.sort(key = lambda x: (x[1], x[0]))

end = time[0][1]
count = 1

for i in range(1, N):
  if time[i][0] >= end or time[i][0] == time[i][1]:
    count += 1
    end = time[i][1]

print(count)

백준 1449 수리공항승

문제

항승이는 품질이 심각하게 나쁜 수도 파이프 회사의 수리공이다. 항승이는 세준 지하철 공사에서 물이 샌다는 소식을 듣고 수리를 하러 갔다.

파이프에서 물이 새는 곳은 신기하게도 가장 왼쪽에서 정수만큼 떨어진 거리만 물이 샌다.

항승이는 길이가 L인 테이프를 무한개 가지고 있다.

항승이는 테이프를 이용해서 물을 막으려고 한다. 항승이는 항상 물을 막을 때, 적어도 그 위치의 좌우 0.5만큼 간격을 줘야 물이 다시는 안 샌다고 생각한다.

물이 새는 곳의 위치와, 항승이가 가지고 있는 테이프의 길이 L이 주어졌을 때, 항승이가 필요한 테이프의 최소 개수를 구하는 프로그램을 작성하시오. 테이프를 자를 수 없고, 테이프를 겹쳐서 붙이는 것도 가능하다.

입력

첫째 줄에 물이 새는 곳의 개수 N과 테이프의 길이 L이 주어진다. 둘째 줄에는 물이 새는 곳의 위치가 주어진다. N과 L은 1,000보다 작거나 같은 자연수이고, 물이 새는 곳의 위치는 1,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 항승이가 필요한 테이프의 개수를 출력한다.

기준

테이프 하나가 커버할 수 있는 범위에 최대한 많이 집어 넣는 것

테이프 길이 L 이 주어졌을 때 좌우 0.5 만큼 간격을 줘야 물이 새지 않으니 테이프 하나는 L - 1 까지 커버가 가능하다. 그러니 n 에서 시작하면 n + L - 1 까지의 구멍을 막아줄 수 있고 다음 n 이 그보다 크면 새로운 테이프를 붙이는 방식으로 접근한다.

풀이

import sys

N, L = map(int, sys.stdin.readline().rstrip().split())
nums = list(map(int, sys.stdin.readline().rstrip().split()))

# 오름차순 정렬
nums.sort()

count = 1
cur = nums[0] + L - 1

for num in nums:
  if num > cur:
    count += 1
    cur = num + L - 1

print(count)

list 연산에 따른 시간 복잡도

시간 복잡도가 O(1) 인 연산

len(a)

a = [1,2,3,4]
print(len(a)) # 4

a[i]

a = [1,2,3,4]
print(a[1]) # 2

a.append(x)

a = [1,2,3,4]
a.append(5)
print(a) # [1, 2, 3, 4, 5]

a.pop()

a = [1, 2, 3, 4]
print(a.pop()) # 4

시간 복잡도가 O(k) 인 연산

a[i:j]

a = [1, 2, 3, 4]
print(a[1:2]) # [2]

시간 복잡도가 O(n) 인 연산

x in a

a = [1, 2, 3, 4]
print(3 in a) # True

a.count(x)

a = [1, 1, 2, 2, 3]
print(a.count(1)) # 2

a.index(x)

a = [1, 2, 3, 4, 5]
print(a.index(4)) # 3

일치하는 값이 다수 있더라도 앞에서부터 가장 먼저 나오는 값의 인덱스를 반환

a.insert(idx, x)

a = [1, 2, 3, 4]
a.insert(2, 5)
print(a) # [1, 2, 5, 3, 4]

append 가 O(1) 인데 비해 insert 가 O(n) 인 이유는 중간에 원소를 삽입한 뒤, 리스트의 원소 위치를 조정해줘야 하기 때문이다.

a.pop(0)

a = [1, 2, 3, 4]
print(a.pop(0)) # 1

pop() 은 O(1) 이나 pop(0) 은 맨 앞에 있는 값을 출력하기 위해 전체 복사를 해주기 위해 O(n) 이 나온다. O(1) 로 처리하기 위해서 deque 를 사용한다.

from collections import deque

data = deque([2, 3, 4])
print(data.popleft()) # 2
data.appendleft(1) # data = deque([1, 3, 4])
data.append(0) # data = deque([1, 3, 4, 0])
print(list(dat)) # [1, 3, 4, 0]

deque 연산자

• appendleft(x) - 첫 번째 인덱스에 원소 x 삽입
• append(x) - 마지막 인덱스에 원소 x 삽입
• popleft() - O(1), 첫 번째 원소 제거
• pop() - 마지막 원소 제거

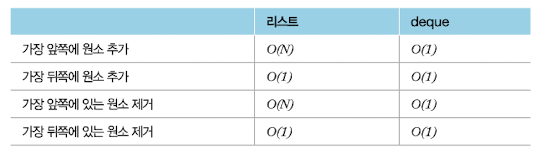
이미지 출처 : 이것이 취업을 위한 코딩 테스트다 with 파이썬

위의 사진에서 deque 에 해당하는 연산자가 차례대로 appendleft(x), append(x), popleft(), pop() 이고
list 에 해당하는 연산자가 차례대로 insert(0, x), append(x), pop(0), pop() 이다.

deque 연산자의 시간복잡도

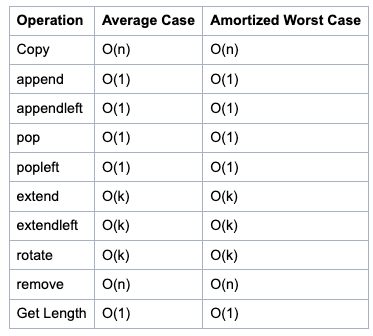
이미지 출처 : python wiki

list 연산자의 시간복잡도

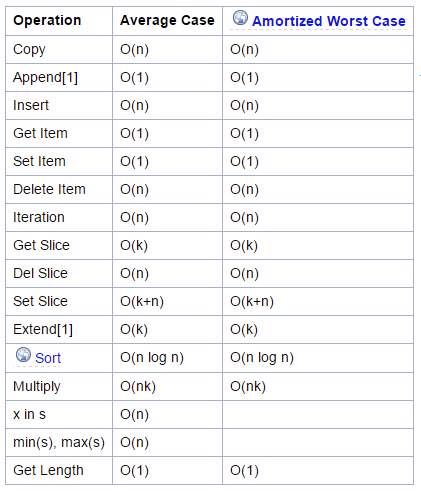
이미지 출처 : python wiki

del a[i]

a = [1, 2, 3, 4]
del a[2]
print(a) # 3

remove(x)

a = [1, 1, 2, 3, 4]
a.remove(1)
print(a) # [1, 2, 3, 4]

특정한 값을 갖는 원소를 제거하나 값을 가진 원소가 여러 개일 경우 하나만 제거한다.

만약 특정한 값의 원소를 모두 제거하려면 다음과 같은 방법을 사용한다.

a = [1, 2, 3, 4, 5, 5, 5]
remove_set = {3, 5}

result = [i for i in a if i not in remove_set]
print(result) # [1, 2, 4]

min(a), max(a)

a = [1, 2, 3, 4]
print(min(a)) # 1
print(max(a)) # 4

a.reverse()

a = [1, 2, 3, 4]
a.reverse()
print(a) # [4, 3, 2, 1]

만약 내림차순으로 정렬하여 출력한다고 하면 a.sort(reverse=True) 는 O(nlogn) 이고 reverse() 는 O(n) 이니 reverse() 가 더 성능이 좋다.

시간 복잡도가 O(nlogn) 인 연산

a.sort()

a = [5, 2, 3 ,1, 4]
a.sort()
print(a) # [1, 2, 3, 4, 5]

sort() 는 TImSort ( Merge Sort + Insert Sort ) 이며 최소 O(n), 최대 O(nlogn) 의 시간복잡도를 보인다.

set 연산에 따른 시간 복잡도

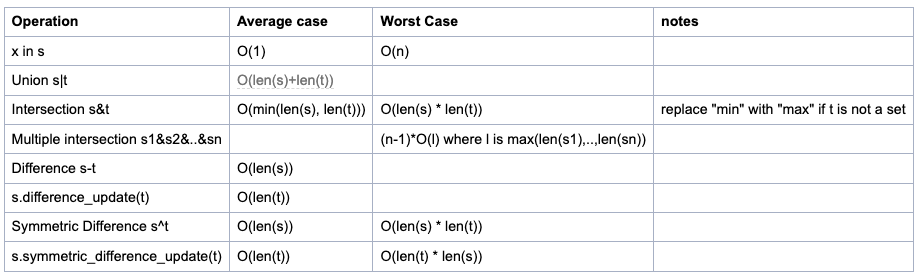
이미지 출처 : python wiki

set 의 add(), remove() 함수의 시간복잡도는 O(1) 이다. - 이것이 취업을 위한 코딩 테스트다 with 파이썬

만약 x in s 연산이 필요한 경우 리스트는 평균 O(n), set 는 평균 O(1), 최악 O(n) 이 소요되니 성능상 set 의 이점이 크다.

dict 에서의 x in x 역시 평균 O(1), 최악 O(n) 이 소요된다.

만약 remove / del 연산이 필요한 경우 리스트는 평균 O(n), set 는 O(1)이 소요되니 성능상 set 의 이점이 크다.

dict 연산에 따른 시간 복잡도

이미지 출처 : python wiki

list, set, dict 에 따라 시간 복잡도를 비교한 다음 2dowon 님의 포스트를 참고하자
2dowon.github.io - list, set, dict 자료형에 따른 시간 복잡도 비교

추가) 유용한 접근법

list 에서의 x in a 는 O(n)
set, dict 에서의 x in a 는 O(1)
dict 에서의 a.get(x) 는 O(1) 이다.

그래서 백준 특유의 둘째 줄에는 정수가 한칸씩 띄어져서 나타난다... 같은 경우 보통 split() 해서 리스트로 저장해왔는데 알고리즘 스터디 팀원분의 코드에서 해시테이블인 dict 로 바로 저장하여 사용하는 방식이 있어 기록하려 한다.

import sys

N, C = map(int, sys.stdin.readline().split()) # N, C
weights = {x : x for x in sorted(list(map(int, sys.stdin.readline().split()))) if x <= C}

위와 같은 코드인데 특정 조건을 만족하는 경우 dict 에 값을 저장하는 방식이다. key: value 모두 x 로 동일한데 어차피 해당 문제 내에서는 value 를 조회하지 않고 key 가 존재하는지 여부만 판단하고 있어 list 의 x in a 보다 더 성능이 좋게 접근할 수 있는 방식이다.

출처

blog
hyun-am - Python list 연산에 따른 시간 복잡도
2dowon.github.io - list, set, dict 자료형에 따른 시간 복잡도 비교
docs
python wiki