서론

이전에 비트마스킹 알고리즘에 대해 알아본 뒤로 새로 알게된 사항들에 대해 정리하고자 한다.

본론

leetcode 67. Add Binary

leedcode 67. add binary

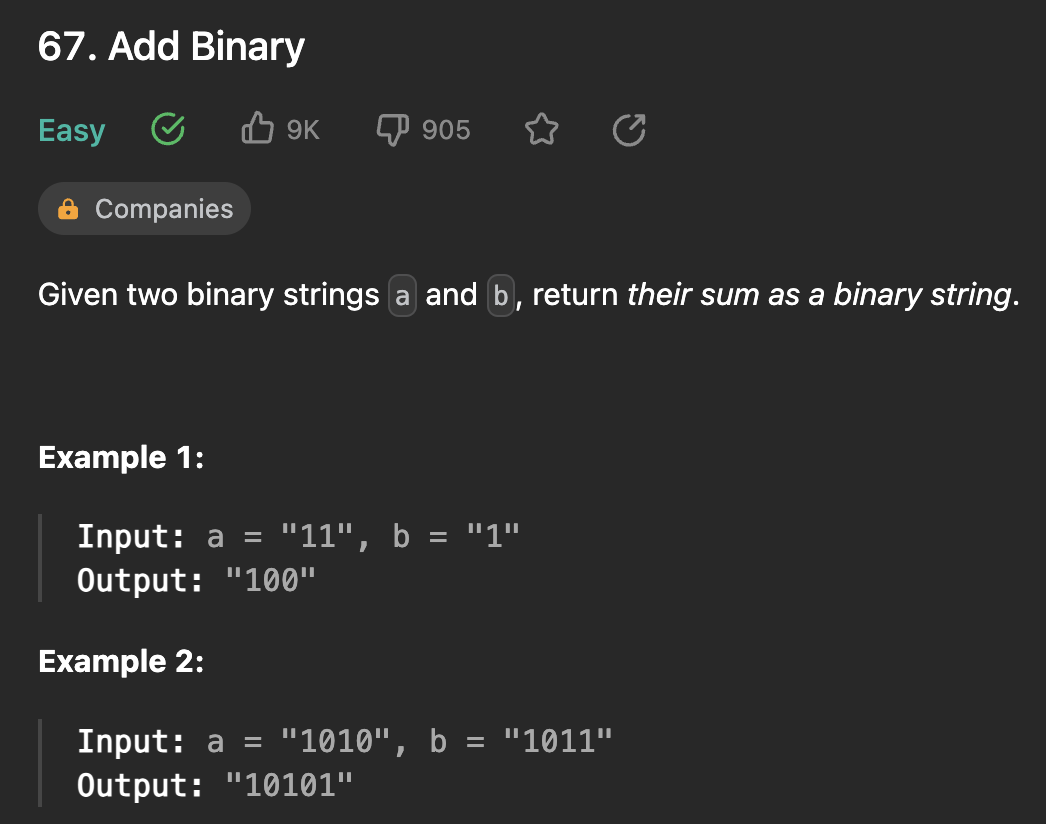
두개의 숫자로 이루어진 문자열을 더할때의 결과를 이진 문자열로 반환하라는 문제이다. 이 문제를 푸는 세가지 방식에 대해 정리하고자 한다.

1. 숫자로 바꿔 더한뒤 다시 이진 문자열로 변환

def addBinary(self, a: str, b: str) -> str:
    result = bin(int(a, 2) + int(b, 2))
    return result[2:]

1. 새로 알게 된 사항 숫자로 이루어진 문자열을 10진수로 바꾸고 싶다면 int 로 감쌀때 두번째 인자로 어떤 k 진수에서 10진수로 바꿀 것인지 나타낼 수 있다.

a = '101'
int(a, 2) # 5

b = '11'
int(b, 3) # 4

2. 새로 알게 된 사항 10진수를 2진수로 변환하는 간단한 방법으로 bin 메서드를 활용하는 방법이 있다. 단, 이때 2진수로 변환한 것이라 앞에 0b 가 붙은 문자열을 반환한다.

a = 5
binary = bin(a) # '0b101'
result = binary[2:] # '101'

=> 위의 풀이는 간단하게 이 문제를 풀 수 있다. 그런데 이 문제는 비트마스킹을 사용해 푸는 것을 요구하고 있다.

2. 비트마스킹을 이용한 풀이

def addBinary(self, a: str, b: str) -> str:
	int_a = int(a, 2)
    int_b = int(b, 2)

	def addBin(int_a, int_b):
    	if int_b == 0: return int_a

		sum_bit = int_a ^ int_b      # xor : 둘중 하나에만 포함된 원소 -> 2
        carry = (int_a & int_b) << 1 # 둘다 포함된 원소들 집합을 1bit 만큼 left shift
        return addBin(sum_bit, carry)

	return bin(addBin(int_a, int_b))[2:]

비트끼리의 덧셈이 어떻게 이루어지는지 생각해보자.
같은 자리의 수가 둘다 1일 경우 carry 가 1 발생한다.
XOR 연산은 (^) 두 수가 다를때 1, 같을때 0 을 반환한다.
AND 연산은 (&) 두 수가 모두 1일때 1을 반환한다.

처음에 어떻게 코드가 작동하는지 살펴보자.

첫 예시인 a = '11', b = '1' 의 경우를 생각해보자.

앞에서 찾아본 것처럼 int(a, 2) = 3, int(b, 2) = 1 이 나온다.
그럼 addBin() 에 두 개의 인자로 3, 1 을 전달한다.

3 과 1 을 XOR 연산하면 어떻게 될까?
11 과 01 을 XOR 연산하면 10 이 반환된다. sum_bit = 10 = 2

3 과 1 을 AND 연산하면?
11 과 01 을 AND 연산하면 01 이 반환된다. 이걸 1 만큼 left shift 해주면 carry = 10 (2) 이다.

그 다음 addBin 에는 2, 2 를 전달한다.

그럼 이때의 동작을 살펴보자.
sum_bit = 10 XOR 10 = 00
carry = (10 AND 10) << 1 = 10 << 1 = 100

그 다음의 동작은 다음과 같다.
sum_bit = 0 XOR 100 = 100
carry = (0 AND 100) << 1 = 0 << 1 = 0

마지막 로직에서 int_b = 0 이 되어 int_a 로 전달된 100 인 4가 반환되고 이를 bin 에 넣었으니 '100' 을 return 에 전달하게 된다.

즉, 두 이진수를 더하는 로직은

1. XOR 연산 ( 일의자리부터 한 자리씩 덧셈 연산 )
2. AND 연산후 1 left shift ( carry 구하기 )
3. 두번째 인자에 0이 전달될 때까지 1 ~ 2를 반복

위의 로직은 한번 반복할 때마다 한자리씩 덧셈을 하며 carry 를 그 다음 자리로 전달한다.

3. 각 인덱스별로 연산한 뒤, 문자열에 직접 더하기

def addBinary(a: str, b: str) -> str:
	ans = ''
    lenA, lenB = len(a) - 1, len(b) - 1
    carry = 0
    
    while lenA >= 0 or lenB >= 0 or carry:
    	if lenA >= 0:
        	carry += int(a[lenA])
            lenA -= 1
        if lenB >= 0:
        	carry += int(a[lenB])
            lenB -= 1
        ans = str(carry % 2) + ans
        carry //= 2
    return ans

leetcode 190. Reverse Bits

leetcode 190. Reverse Bits

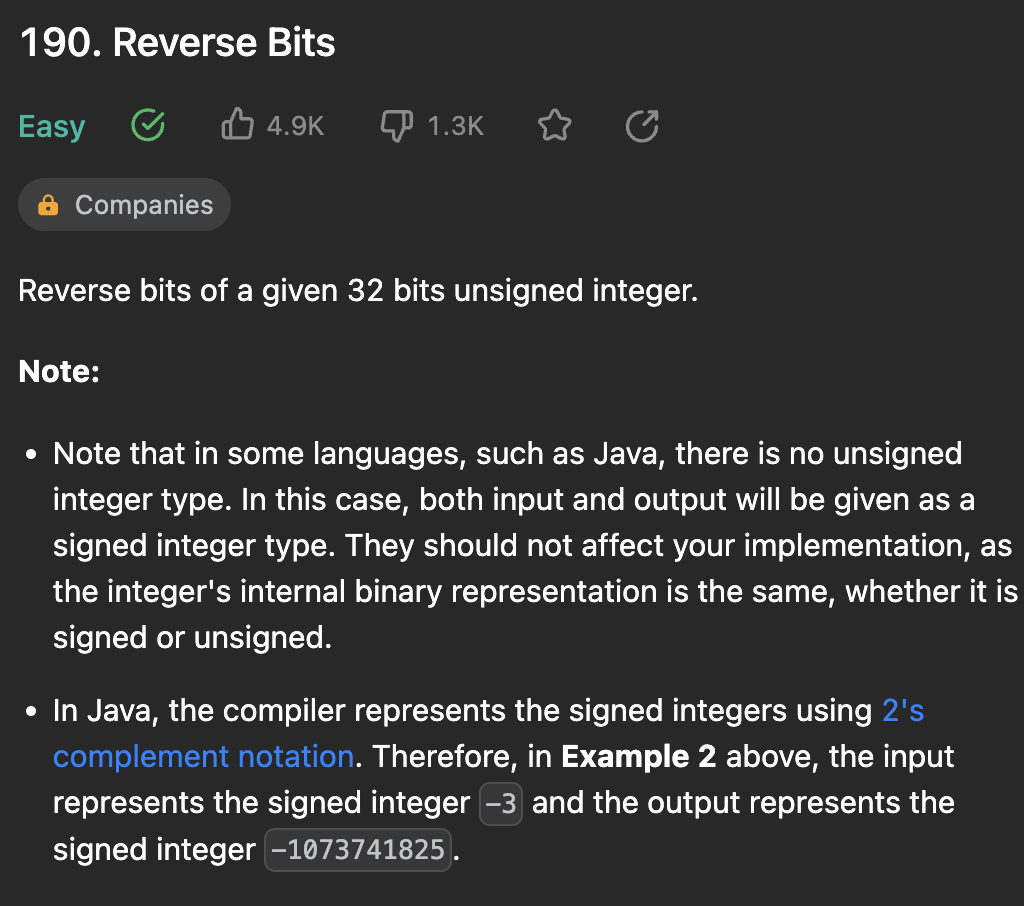
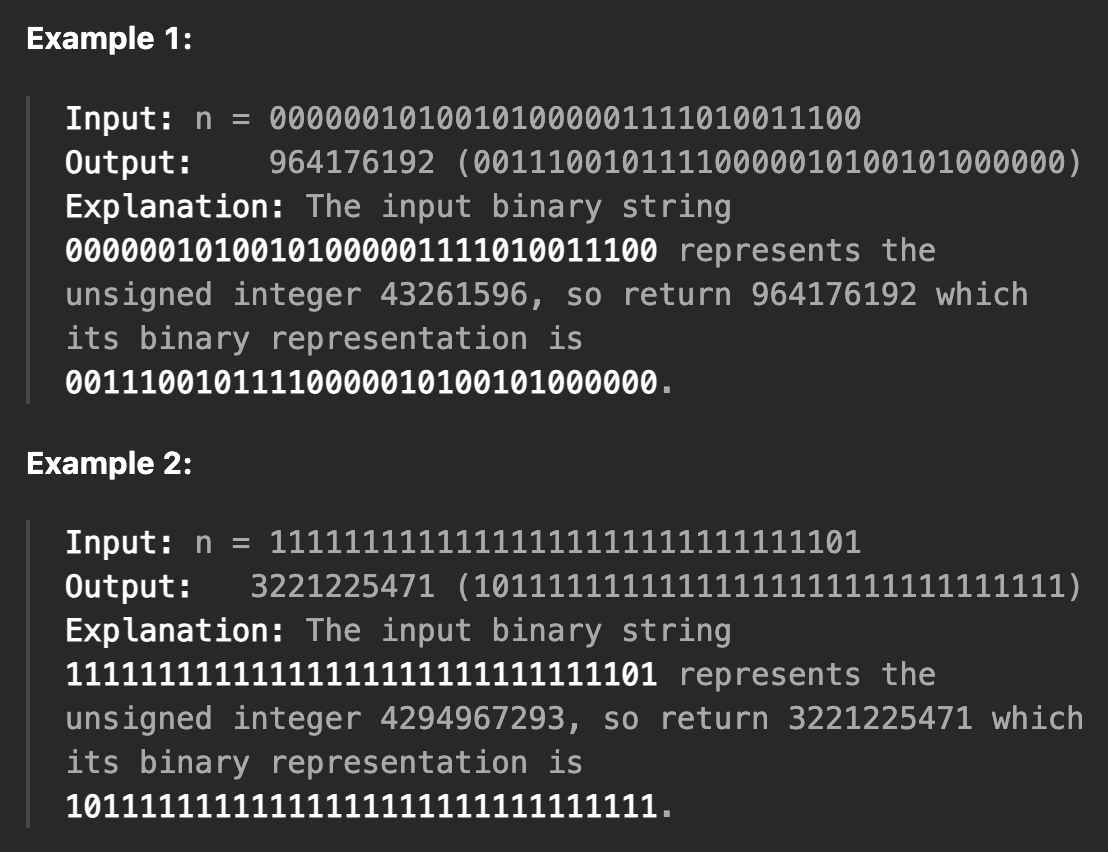
주어진 10진수를 2진수로 볼때 반전해서 32비트로 나타내면 그때의 10진수를 반환하라는 문제다.

풀이 1.

def reverseBits(self, n: int) -> int:
    string = bin(n)[2:] # 3 -> '0b11' -> string = '29 * 0 110'
    reverse_string = string[::-1] # '011 29 * 0'

    gap = 32 - len(reverse_string)

    if gap != 0:
        for _ in range(gap):
            reverse_string = reverse_string + '0'

    return int(reverse_string, 2)

이 풀이 역시 비트마스킹을 쓰지 않았다.

풀이 2.

def reverseBits(self, n: int) -> int:
    n = format(n, 'b')
    n = n.zfill(32)
    return int(n[::-1], 2)

format 에 두번째 인자로 'b', 'x', 'o' 를 붙이는 것에 따라 해당 10진수를 k 진수로 변환할 수 있다.

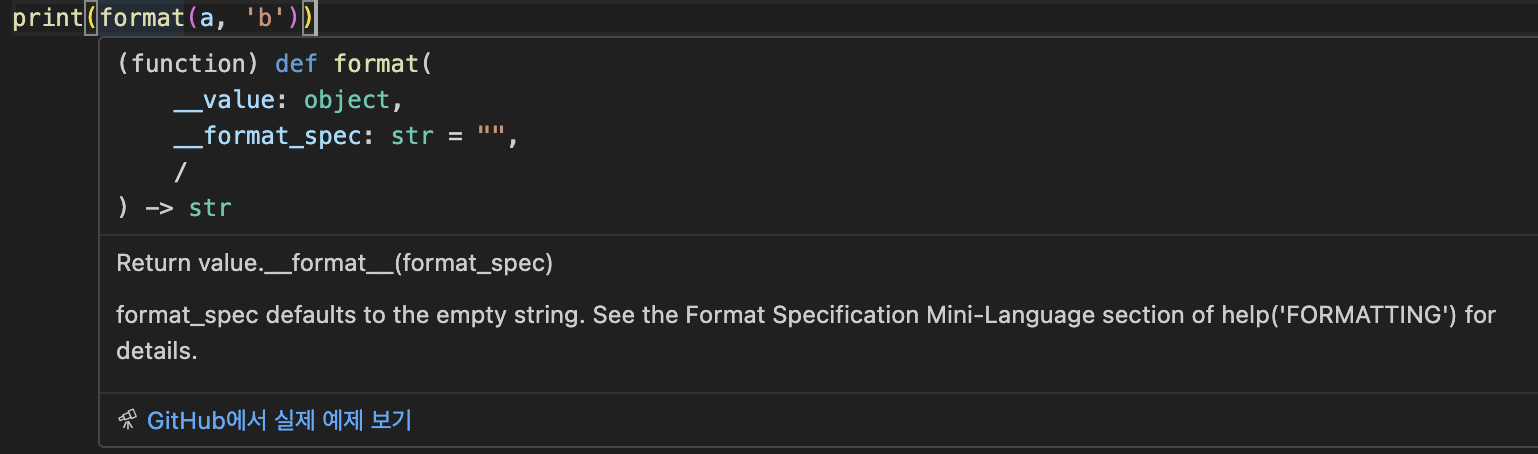
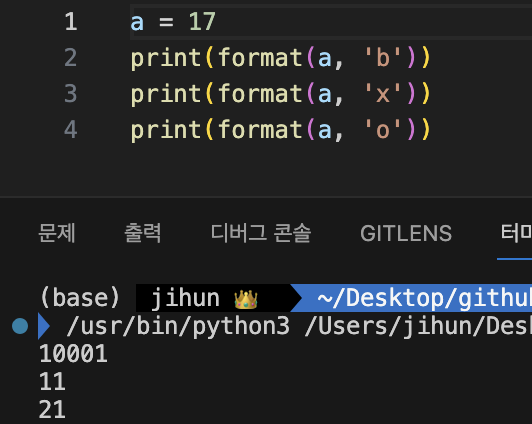
3. 새로 알게 된 사항 format 에 두번째 인자를 전달해 10진수를 간편하게 다른 진수로 변환할 수 있다.

zfill 은 인자로 전달한 수보다 n 의 길이가 짧으면 부족한 만큼 0으로 채워준다.

4. 새로 알게 된 사항 zfill 은 부족한만큼 0을 채워준다.

=> 사실 이 문제는 비트마스킹을 이용한 풀이가 있는데 아직 잘 이해가 안돼서 이해가 잘 되면 그때 정리하려고 한다.

leetcode 191. Number of 1 Bits

leetcode 191. Number of 1 Bits

1 의 개수를 반환하라는 문제다.

def hammingWeight(self, n: int) -> int:
    ans = 0

    while(n != 0):
        n = n & (n - 1)
        ans += 1

    return ans

풀이가 신박해서 같이 코딩테스트 스터디하시는 분의 풀이를 가져왔다.

n = 110 일때를 생각해보자.
n - 1 = 101 이다.
이 둘을 AND 연산하면 100 이다.
즉, 어떤 수와 해당 수에서 1을 뺀 두 수를 AND 연산할 때마다 가장 끝의 1이 0으로 바뀌며 1의 수를 카운트 할 수 있다.

추후 참고

비트마스킹 정리 - 1998yuki0331
파이썬 코딩도장 비트 연산자