링크

문제 링크

문제 설명

N개의 아파트가 일렬로 쭉 늘어서 있습니다. 이 중에서 일부 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 기술이 발전해 5g 수요가 높아져 4g 기지국을 5g 기지국으로 바꾸려 합니다. 그런데 5g 기지국은 4g 기지국보다 전달 범위가 좁아, 4g 기지국을 5g 기지국으로 바꾸면 어떤 아파트에는 전파가 도달하지 않습니다.

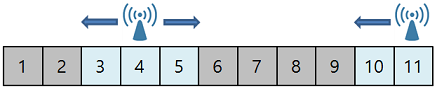
예를 들어 11개의 아파트가 쭉 늘어서 있고, [4, 11] 번째 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 만약 이 4g 기지국이 전파 도달 거리가 1인 5g 기지국으로 바뀔 경우 모든 아파트에 전파를 전달할 수 없습니다. (전파의 도달 거리가 W일 땐, 기지국이 설치된 아파트를 기준으로 전파를 양쪽으로 W만큼 전달할 수 있습니다.)

• 초기에, 1, 2, 6, 7, 8, 9번째 아파트에는 전파가 전달되지 않습니다.

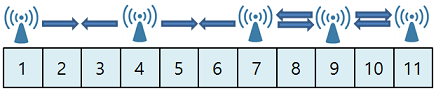
• 1, 7, 9번째 아파트 옥상에 기지국을 설치할 경우, 모든 아파트에 전파를 전달할 수 있습니다.

• 3개의 아파트보다 더 많은 아파트 옥상에 기지국을 설치할 경우에도 모든 아파트에 전파를 전달할 수 있습니다.

이때, 우리는 기지국을 최소로 설치하면서 모든 아파트에 전파를 전달하려고 합니다. 위의 예시에선 최소 3개의 아파트 옥상에 기지국을 설치해야 모든 아파트에 전파를 전달할 수 있습니다.

아파트의 개수 N, 현재 기지국이 설치된 아파트의 번호가 담긴 1차원 배열 stations, 전파의 도달 거리 W가 매개변수로 주어질 때, 모든 아파트에 전파를 전달하기 위해 증설해야 할 기지국 개수의 최솟값을 리턴하는 solution 함수를 완성해주세요

제한사항

• N: 200,000,000 이하의 자연수
• stations의 크기: 10,000 이하의 자연수
• stations는 오름차순으로 정렬되어 있고, 배열에 담긴 수는 N보다 같거나 작은 자연수입니다.
• W: 10,000 이하의 자연수

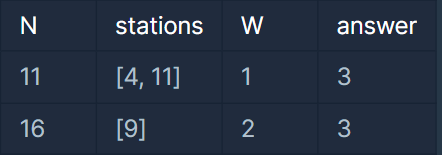
입출력 예

입출력 예 설명

입출력 예 #1
문제의 예시와 같습니다

입출력 예 #2

• 초기에, 1~6, 12~16번째 아파트에는 전파가 전달되지 않습니다.

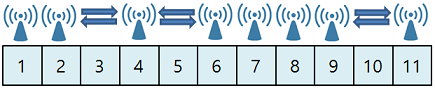
• 3, 6, 14번째 아파트 옥상에 기지국을 설치할 경우 모든 아파트에 전파를 전달할 수 있습니다.

풀이

1. w는 양쪽으로 퍼지기 때문에, begin과 end지점사이에 2w+1이 얼마나 많이 들어갈 수 있는지 구하자.
2. begin과 end는 처음에 begin은 1로, end는 stations[i] - w - 1로 잡자
3. 반복문이 끝나고나서 뒷 부분에 만약 전파가 닿지 않는다면, 추가적으로 더 계산해주면 끝!

이 문제는 처음에 무조건 이분탐색인줄 알고 구간마다 이분탐색을 썼다.

내가 만든 테스트케이스는 다 통과했지만, 제출시 절대 통과되지 않는 테스트케이스들이 많았다. 한.. 6개정도?

그래서 여러 경우를 생각하는 과정에서 이분탐색적으로 접근했을 때 한 가지 문제점을 발견할 수 있었다.

예를 들어 범위가 1 ~ 10까지에 w가 3이라 치자. 이분탐색으로 설치하면 1과 10의 중간인 5에 설치하고, 양쪽에 닿지않는 곳에 또 설치를 하면 총 3개가 요구된다.

그러나 연습장에 그려봤을때, 4에 설치하면 123(4)567 까지 전파를 미칠 수 있고 8,9,10은 그냥 아무데나 한 군데 설치하면 된다. 즉 2개가 요구되었다.

즉 이분탐색으로 접근한 나의 실책이었다.

그래서 생각을 달리하여 두 지점사이에, 2w + 1이 몇개가 들어갈 수 있을까? 를 계산하였고, 나머지가 있다면, 리턴하기 전 ++해주고 리턴해주니까 바로 통과되었다..

(왜 2w+1이냐면, 기지국을 기준으로, 양쪽으로 w가 퍼지기때문에, 2w에 기지국 1개까지 총 2w+1이라 생각했다.)

코드

class Solution {
    public int bsearch(int begin, int end, int w) {
        int res = (end - begin + 1) / (2 * w + 1);
        if((end - begin + 1) % (2 * w + 1) > 0) res++;
        return res;
    }
    public int solution(int n, int[] stations, int w) {
        int answer = 0;
        int begin = 1;
        for(int i = 0; i < stations.length; i++) {
            if(begin < stations[i] - w)
                answer += bsearch(begin, stations[i] - w - 1, w);
            begin = stations[i] + w + 1;
        }
        if(stations[stations.length - 1] + w < n)
            answer += bsearch(stations[stations.length - 1] + w + 1, n, w);
        return answer;
    }
}