문제링크

문제 링크

문제 설명

제한 사항

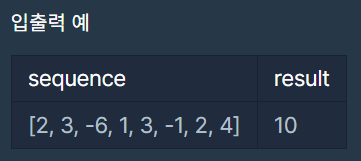
입출력 예

입출력 예 설명

풀이

1. 제한사항에 sequence의 길이가 50만까지니까, O(n)들로만 구성된 반복문만 쓴다면 딱히 풀이에 지장이 없을것이라 생각했다.
2. 모든 sequence 배열 각 원소에 1 -1을 곱해서, 그 합을 누적하여 쌓은 배열 하나를 가지고있자
3. 그 배열의 최댓값 - 최솟값이 곧 문제의 정답!

처음에 문제를 잘못읽어서 음과양 또는 양과음이 연속해서 반복되는 구간의 처음과 끝을 잘랐다.

그리고 거기에 펄스 수열을 곱해서 그렇게 나온 수들의 최댓값을 구했었는데 제출하니까 빨간거만 보이길래 ㅜ 문제를 다시 심오하게 읽고 풀었다!

그리고 누적합 배열 구할때 1, -1, 1, -1을 곱해서 나온 sum이나 -1, 1, -1, 1을 곱해서 나온 sum이나 양음만 반대되는 값이 나온다는 것을 알았다!

그래서 제출된 코드에는 두가지 타입의 펄스 모두 2차원 배열의 long[][] sum에 담았지만, 타입 하나만 쓰면 되는것을 알고나서 조금 수정했다.

여기다 쓰는것은 수정된 코드인 long 타입 1차원 sum 배열이다.

코드

import java.util.*;
class Solution {
    public long maxMinusMin(long[] sum) {
        long max = -100001;
        long min = 100001;
        for(int i = 0; i < sum.length; i++) {
            if(max < sum[i])
                max = sum[i];
            if(min > sum[i])
                min = sum[i];
        }
        return Math.abs(max - min);
    }
    public long solution(int[] sequence) {
        long answer = 0;
        long[] sum = new long[sequence.length + 1];
        for(int i = 1; i < sum.length; i++)
        {
            if(i % 2 == 0) {
                sum[i] = sum[i - 1] + (long) sequence[i - 1] * -1;
            }
            else {
                sum[i] = sum[i - 1] + (long) sequence[i - 1];
            }
        }
        answer = maxMinusMin(sum);
        return answer;
    }
}