링크

문제 링크

문제 설명

OO 연구소는 한 번에 K 칸을 앞으로 점프하거나, (현재까지 온 거리) x 2 에 해당하는 위치로 순간이동을 할 수 있는 특수한 기능을 가진 아이언 슈트를 개발하여 판매하고 있습니다. 이 아이언 슈트는 건전지로 작동되는데, 순간이동을 하면 건전지 사용량이 줄지 않지만, 앞으로 K 칸을 점프하면 K 만큼의 건전지 사용량이 듭니다. 그러므로 아이언 슈트를 착용하고 이동할 때는 순간 이동을 하는 것이 더 효율적입니다. 아이언 슈트 구매자는 아이언 슈트를 착용하고 거리가 N 만큼 떨어져 있는 장소로 가려고 합니다. 단, 건전지 사용량을 줄이기 위해 점프로 이동하는 것은 최소로 하려고 합니다. 아이언 슈트 구매자가 이동하려는 거리 N이 주어졌을 때, 사용해야 하는 건전지 사용량의 최솟값을 return하는 solution 함수를 만들어 주세요.

예를 들어 거리가 5만큼 떨어져 있는 장소로 가려고 합니다.
아이언 슈트를 입고 거리가 5만큼 떨어져 있는 장소로 갈 수 있는 경우의 수는 여러 가지입니다.

처음 위치 0 에서 5 칸을 앞으로 점프하면 바로 도착하지만, 건전지 사용량이 5 만큼 듭니다.
처음 위치 0 에서 2 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 2) x 2에 해당하는 위치로 이동할 수 있으므로 위치 4로 이동합니다. 이때 1 칸을 앞으로 점프하면 도착하므로 건전지 사용량이 3 만큼 듭니다.
처음 위치 0 에서 1 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 1) x 2에 해당하는 위치로 이동할 수 있으므로 위치 2로 이동됩니다. 이때 다시 순간이동 하면 (현재까지 온 거리 : 2) x 2 만큼 이동할 수 있으므로 위치 4로 이동합니다. 이때 1 칸을 앞으로 점프하면 도착하므로 건전지 사용량이 2 만큼 듭니다.
위의 3가지 경우 거리가 5만큼 떨어져 있는 장소로 가기 위해서 3번째 경우가 건전지 사용량이 가장 적으므로 답은 2가 됩니다.

제한 사항

• 숫자 N: 1 이상 10억 이하의 자연수
• 숫자 K: 1 이상의 자연수

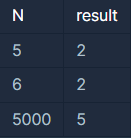
입출력 예

입출력 예 설명

입출력 예 #1
위의 예시와 같습니다.

입출력 예 #2
처음 위치 0 에서 1 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 1) x 2에 해당하는 위치로 이동할 수 있으므로 위치 2로 이동합니다. 이때 1 칸을 앞으로 점프하면 위치3으로 이동합니다. 이때 다시 순간이동 하면 (현재까지 온 거리 : 3) x 2 이동할 수 있으므로 위치 6에 도착합니다. 이 경우가 건전지 사용량이 가장 적으므로 2를 반환해주면 됩니다.

입출력 예 #3
위와 같은 방식으로 합니다.

풀이

1. 현재의 거리에서 순간이동(현재 거리 X 2)는 비용 발생 X
2. 1번을 생각해보면 현재 N이 만약 짝수라면 N/2와의 비용(정답)이 같을 것이다.
3. 만약 홀수라면 비용 하나를 소모해서 N을 짝수로 만들어주고 2번을 반복하자
4. 3번의 과정에서 비용 하나를 소모할때 ans를 하나 올려주자
5. N이 1이 될때까지!

처음에는 이 문제가 메모이제이션 dp인가 생각하다가 N이 10억이하의 자연수인것을 보고 바로 후퇴하였다.

소인수분해인가? 라는 생각도 짧게 해보았다. 그러다 잠시 생각해보니 구하려는 N의 비용은 N/2에서 순간이동을 하면 되지 않겠나?

그 N/2는 N/4에서 순간이동을 하면 되지 않겠나? 라는 생각을 반복하였고 값이 홀수가 될때마다 비용을 하나씩 소모해서 짝수로 맞춰주는 과정일까? 생각하다가 그 과정이 옳았음을 깨닫게 되었다.

나는 근데 여기서 항상 의심병이 도져서 직접 구현해보기도 전에 "진짜 그게 최소일까?"라는 생각을 쓸데없이 한다..

public class Solution {
    public int solution(int n) {
        int ans = 1;
        
        while(n > 1){
            if(n % 2 == 0)
                n /= 2;
            else {
                n--;
                ans++;
            }
        }
        
        return ans;
    }
}

이게 내 코드지만 풀고나서 질문하기를 통해 당연하지만 당시 나한텐 당연하지 못했던 아이디어를 제공받았다.

이곳이 내가 영감을 얻은 곳인데, 저 코드에서 조금만 변환시키면 정수를 이진수로 변환하는 과정이며 결국 나는 True 비트의 개수를 세고있었다.

마침 정수를 이진수로 나타냈을 때 1의 개수를 구하는 메소드 bitCount()를 알고있었기에 코드를 한 번 더 수정해보았다.

public class Solution {
    public int solution(int n) {
        return Integer.bitCount(n);
    }
}

엄청 깔끔하게 변했다...