[Array] Find pivot index

Find pivot index 문제는 피봇을 찾으라는 문제입니다.
어떤 피봇을 말하냐면 피봇을 기점으로 왼쪽 수의 합과 오른쪽 수의 합이 같은 곳의 중간에 위치한 피봇입니다. 피봇을 발견했다면 피봇의 인덱스를 리턴하고, 만약 피봇을 발견하지 못했다면 -1을 리턴하면 됩니다.

투 포인트와 슬라이딩 윈도우 알고리즘

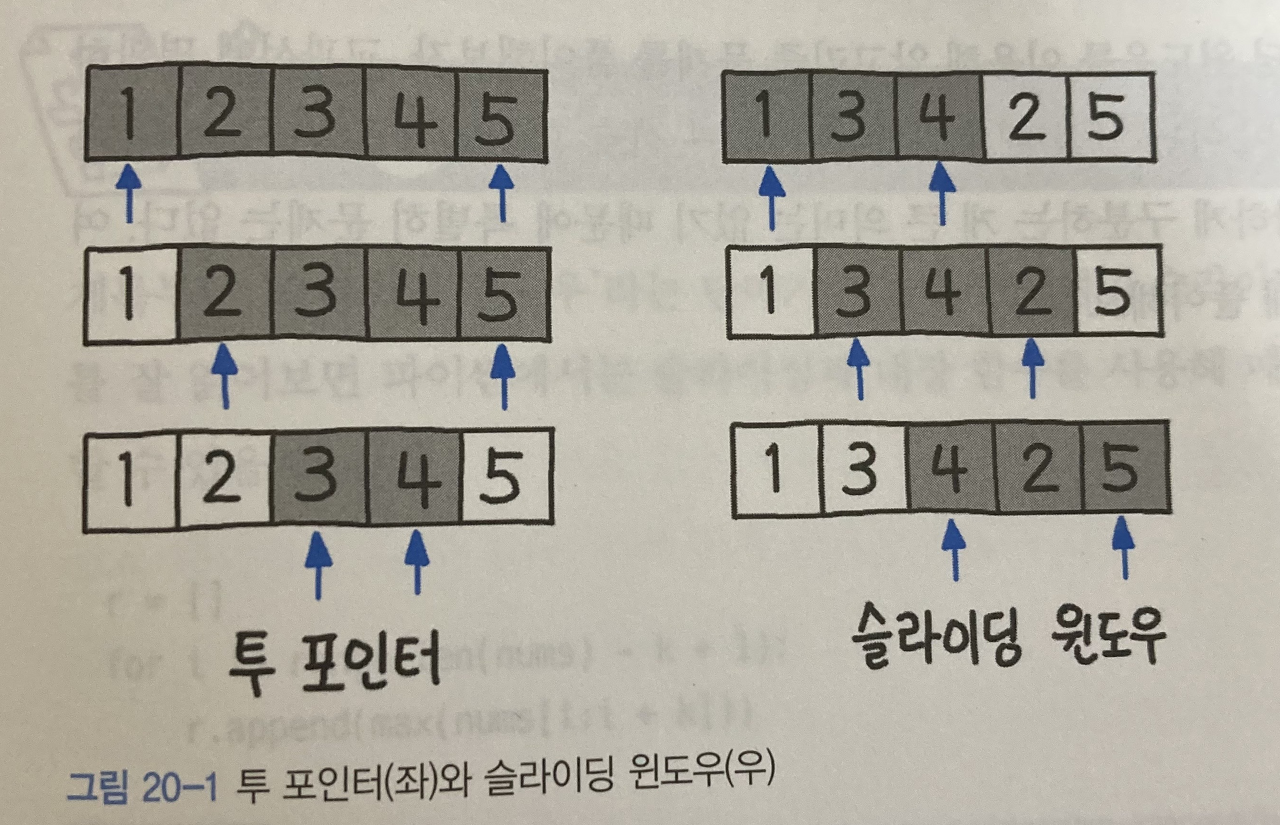
슬라이딩 윈도우는 고정 사이즈의 윈도우가 이동하면서 윈도우 내에 있는 데이터를 이용해 문제를 풀이하는 알고리즘을 말합니다.

투 포인터와 슬라이딩 윈도우 알고리즘은 선형 공간(1차원 배열)을 2회 이상 반복적으로 탐색해야 할 경우 O(N²) 이상 걸릴 시간 복잡도를 부분 배열을 활용하여 O(N)으로 줄일 수 있다는 공통점이 있습니다.

투 포인트 알고리즘은 구간의 넓이가 조건에 따라 유동적으로 변하며,
슬라이딩 윈도우 알고리즘은 항상 구간의 넓이가 고정되어 있다는 차이점이 있습니다.

이 문제를 브루트 포스(완전탐색)알고리즘으로 푼다면 인덱스를 하나하나 피봇으로 잡고 피봇의 왼쪽과 오른쪽을 전부 합쳐봅니다.
인덱스가 증가할 때마다 나머지 인덱스 전체를 돌아다니며 새로운 계산을 진행하기 때문에 O(n^2)의 시간 복잡도를 가집니다.

슬라이딩을 이용한 방법 :

1. 전체 합을 한번 구해줍니다. 이때는 O(n)의 시간이 생깁니다.
2. 배열의 첫번째 인덱스부터 피봇을 잡습니다. 피봇 왼쪽의 합은 0으로 시작하고, 피봇 오른쪽은 전체합에서 피봇 인덱스의 엘리멘트를 빼줍니다. (전체합 - [0]인덱스) 그리고 비교합니다.
3. 해당 인덱스가 피봇이 아니라고 판단했다면 다음 인덱스로 피봇이 넘어갑니다. 이제 피봇 왼쪽의 합은 (0 + [0])이고, 오른쪽의 합은 (전체합 - [0] - [1])이죠.
4. 이렇게 피봇이 나올때까지 비교하고, 피봇이 배열 마지막 인덱스까지 간다면 -1을 리턴하고 반복문을 종료합니다.

슬라이딩을 이용하면 피봇을 증가시킬때마다 새로운 계산을 진행하는것이 아니라, 이미 구해둔 전체합에서 +,- 를 진행하기 떄문에 O(N)의 시간 복잡도로 문제를 풀 수 있습니다.

구현

static int findIndex(int[] nums)
{
    int sum = nums.Sum();
    int leftSum = 0;
    int rightSum = sum;

    int pastPivotNum = 0;
    for (int idx = 0; idx < nums.Length; idx++)
    {
        rightSum = rightSum - nums[idx];
        leftSum = leftSum + pastPivotNum;

        if (leftSum == rightSum)
        {
            return idx;
        }

        pastPivotNum = nums[idx];
    }

    return -1;
}

+) 슬라이딩 추가 문제
209. Minimum Size SubArray Sum
이 문제는 주어진 타겟보다 크거나 같은(sum >= target) subArray를 찾아서
그중 가장 길이가 짧은 subArray의 길이를 반환하는 문제입니다.
(만약 subArray가 없다면 0을 반환합니다.)

예) nums = [2, 3, 1, 2, 4, 3], target = 7이라면
[1,2,4], [4,3]의 subArray를 찾을 수 있고,
[4,3]의 길이가 더 작으니 2를 반환합니다.

예2) nums = [10, 2, 3], target = 6이라면
[10]의 subArray를 찾을 수 있으니 1을 반환합니다.

static int MinSubArrayLen(int[] nums, int target)
{
    int left = 0, right = 0, sum = 0, min = int.MaxValue;
    while (right < nums.Length)
    {
        sum += nums[right];
        right++;
        while (sum >= target)
        {
            min = Math.Min(min, right - left);
            sum -= nums[left];
            left++;
        }
    }
    return min == int.MaxValue ? 0 : min;
}