11729: 하노이 탑 이동순서

어떤 문제인가?

재귀함수로 표현하기 좋도록 문제를 조건별로 나누는 문제.

시행착오 횟수

아마도 4번 정도일텐데, 그 중 옛날에 2번은 손도 못댔다.

1~2차 시도: ???

좀 오래되어서 어떻게 했는지 정확하게는 기억이 나지 않는데, 움직이는 순서를 일렬로 세워놓고 규칙을 찾으려 했으나 실패했었다.

3차 시도: 구상

이번에는 2차원에서 판의 움직임을 보려고 했다. 맨 밑에 있는 판을 1번 판이라고 하고, 그 바로 위에 있는 판은 2번, 그 위는 3번.. 이렇게 번호를 붙이자.

• $N = 1$ 일때
  -> 1) 1 -> 3
• $N = 2$ 일때
  -> 2) 1 -> 2 / 2 -> 3
  -> 1) 1 -> 3
• $N = 3$ 일때
  -> 3) 1 -> 3 / 3 -> 2 / 2 -> 1 / 1 -> 3
  -> 2) 1 -> 2 / 2 -> 3
  -> 1) 1 -> 3

그렇다. $N \geq 3$일때부터 아래 판이 움직이는 것과 똑같이 움직이는 부분이 있다. 나는 이것을 보고서 $N$번째 원판의 이동 순서를 아래처럼 정의하고 문제를 풀려 했다.

여기에서 $f(N)$은 $N$번째 원판의 이동 순서이며, $f'(N)$은 $f(N)$의 정반대 순서이다. 예컨대 위에서의 $N=2$을 예시로 들자면,

$f(2)$ = 1 -> 2 / 2 -> 3
$f'(2)$ = 3 -> 2 / 2 -> 1

이 된다. 근데 필자가 너무 나간 나머지 한가지 중요한 사실을 잊고 말았다. 그래서 하노이 탑 순서는 어떻게 표현하는가? 위 식은 각각의 원반이 움직이는 순서를 나타낼 뿐이지, 전체적인 순서를 나타내주진 않는다.

4차 시도: AC

어떻게든 규칙을 필사적으로 찾으려 애썼는데, 도저히 규칙이 보이질 않았다. 그래프를 그려보면 $N=1$ 을 뿌리로 두는 나무 모양이라, 이를 이용하려고 했는데 그렇게 해도 여전히 전체 순서를 나타낼 수 없었고, 맨 왼쪽 가지부터 시작해서 아래로 타고 내려오는 방식도 소용이 없었다. 자칫하면 $N=1$ 인 경우를 여러 번 표현할 수 있었기 때문이었다.

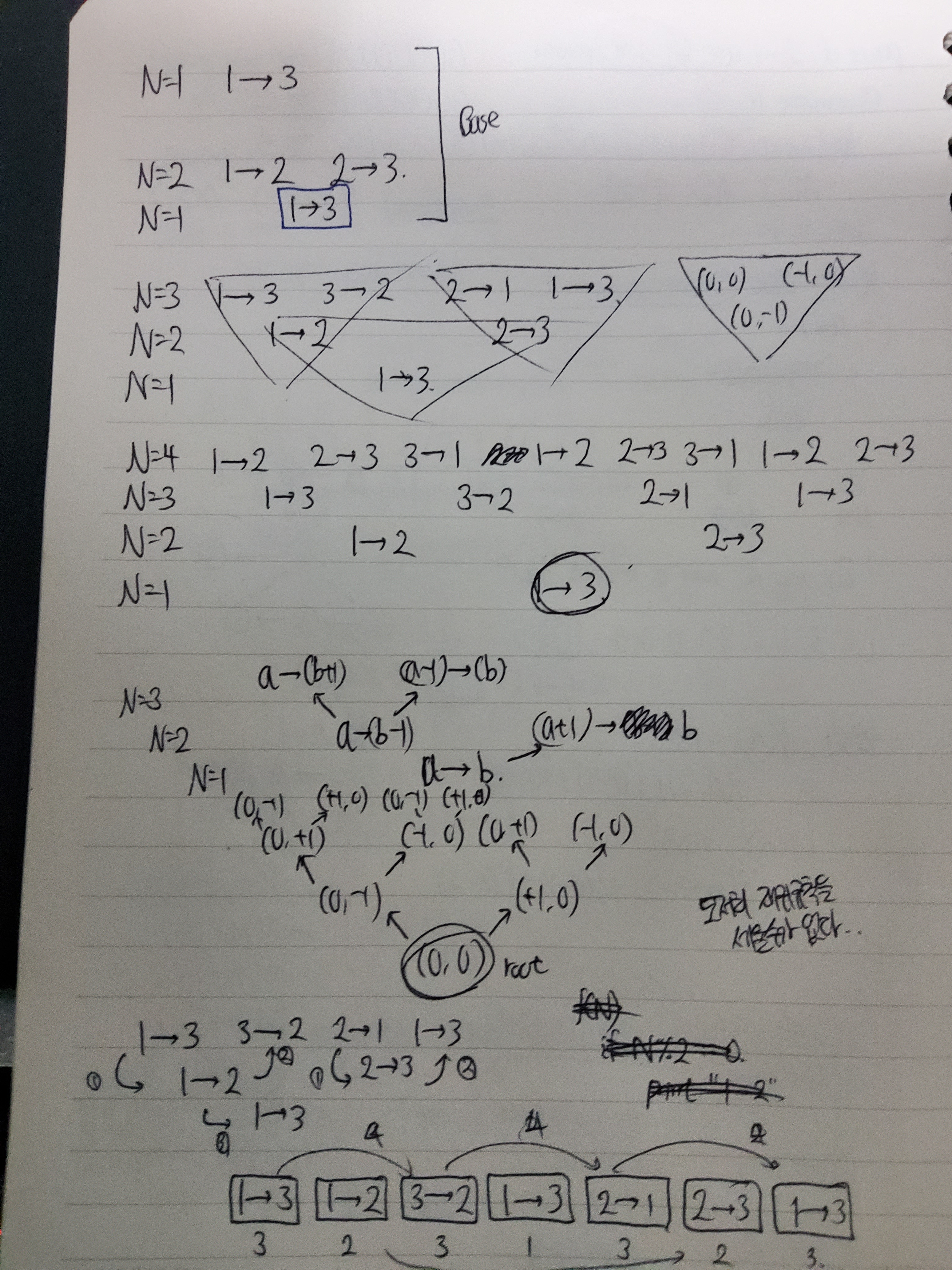
그러던 중, 갑자기 이 생각이 떠올랐다. 전에 했던 것처럼 1차원으로 다시 나열한다면, 반복문을 이용해서 풀 수 있지 않을까 하고 말이다. 배열을 하나 선언하고 한 쌍의 원소를 집어넣기로 했다. 예를 들어 1번에서 3번으로 옮겨야 한다면 배열에는 [1, 3] 처럼 담기로 했다. 1차원 배열에 모조리 넣어야 하기 때문에 [1, 3, 1, 2, 3, 1, 2, ...] 처럼 써야 했다.
여기까지 생각하고 나니 코드를 쓸 수 있었다. 물론 재귀를 쓴 것보단 많이 지저분하다.

#include <stdio.h>

char T[2097152];
int C=0;

int main() {
    int N,k;
    scanf("%d", &N);
    printf("%d\n", (1<<N)-1);
    for(int j=0;j<=N;j++) {
        k = 1;
        for(int i=2*((1<<j)-1); i<2*((1<<N)-1); i+=2<<(j+1)) {
            T[i] = k;
            if((j+N+1)%2==1) {
                k = k >= 3 ? 1 : k + 1;
                T[i+1] = k;
            } else {
                k = k <= 1 ? 3 : k - 1;
                T[i+1] = k;
            }
        }
    }
    for(int i=0;i<2*((1<<N)-1);i+=2)
        printf("%d %d\n", T[i], T[i+1]);
    return 0;
}

지금에서야 이런 생각이 든다. 배열에 안 담고 printf() 만 써서 바로 출력할 수 있었을 것 같다고.
이렇게까지 지저분하게 풀고 나니 과연 재귀로는 어떻게 푸는지 궁금해졌다.

재귀를 이용한 풀이

음.. 처음 이 풀이를 봤을 때 '이게 된다고?' 라는 생각이 먼저 들었다. $N-1$개의 원반을 어디에서 어디쪽으로 옮긴다는 것을 나타내는 3개의 변수만으로 문제를 푸는 것이 아닌가?

아! 그렇다. 필자는 문제를 너무 잘게 쪼개서 봤었다. 이 재귀 알고리즘은 실로 간단하다. 우선 하노이 탑의 조건을 다시 한번 되새겨보자.

1. 작은 원판 위에 큰 원판을 올릴 수 없다.
2. 원판은 한 번에 단 한 개만 옮길 수 있다.

즉, 원반들을 왼쪽에서 오른쪽으로 전부 옮기기 위해서는 맨 밑판부터 차근차근 깔아야 한다. 쉬운 설명을 위해 3개의 원판이 끼워져 있다고 하고, 재귀 알고리즘이 어떻게 작동하는지 보자.

1. 왼쪽 핀에 꽂힌 원반을 위에서부터 2개를 꺼내 중앙에 놓는다.
2. 왼쪽 핀에 마저 남아있는 밑판을 오른쪽으로 옮긴다.
3. 중앙에 끼운 나머지 원반을 우측으로 옮긴다.

... 중간과정이 생략되어 있어서 크게 와닿지 않을 것이다. 특히 필자처럼 하노이 원판을 하나하나씩 옮기는 방법을 생각한 사람이라면 더욱 그럴 것인데, 이렇게 설명해놓으면 하나하나씩 옮겨야 할 원반을 마치 한번에 옮기는 것 같아보이기 때문일 것이다.

이제 잠시 뒤로 물러서서 크게 바라보자. 한꺼번에 이동하는 부분은 사실 여러개의 원판을 이리저리 움직여서 결국에는 중앙에 모두 모은 것에 불과하다. 다시 위 예시를 살펴보자. 1번 동작은 다음 동작이 모여 이뤄진 결과다.

1. 왼쪽에서 맨 오른쪽으로 가장 작은 원판 하나를 옮긴다.
2. 왼쪽에서 가운데로 2번째로 작은 원판 하나를 옮긴다.
3. 오른쪽에서 중앙으로 가장 작은 원판 하나를 옮긴다.

이는 1개 이상의 원판이 끼워진 경우에도 마찬가지다. 핵심은 왼쪽에서 오른쪽으로 탑을 옮기기 위해서는 밑판부터 쌓을 수 밖에 없다는 것이고, 이는 위에서 언급한 규칙을 다르게 설명한 것에 불과할 뿐이다.

그래도 이해가 안 되는가? 재귀 코드를 가지고 직접 하나하나씩 살펴보자.

void hanoi(int num, int start, int mid, int to) {
	if(num == 1) {
      printf("%d %d\n", start, to);
      return;
    }
    
    hanoi(num-1, start, to, mid);
    hanoi(1, start, mid, to);
    hanoi(num-1, mid, start, to);
}

num = 3 이라고 하자. 목표는 3개의 원반을 왼쪽 핀(1번)에서 우측 핀(3번)으로 옮기는 것이다.
즉, 저 함수는 hanoi(3, 1, 2, 3) 으로 처음 실행된다. 저 코드에서 mid 를 직접 참조하는 부분이 없음에 주목하라. 시작점과 끝점만 관심 대상이다.

---

// 위에서부터 아래 순서대로 실행된다.
hanoi(3, 1, 2, 3)

-> hanoi(2, 1, 3, 2)
--> hanoi(1, 1, 2, 3) // 1 3 출력
--> hanoi(1, 1, 3, 2) // 1 2 출력
--> hanoi(1, 3, 1, 2) // 3 2 출력

-> hanoi(1, 1, 2, 3) // 1 3 출력

-> hanoi(2, 2, 1, 3)
--> hanoi(1, 2, 3, 1) // 2 1 출력
--> hanoi(1, 2, 1, 3) // 2 3 출력
--> hanoi(1, 1, 2, 3) // 1 3 출력

규칙에 맞춰서 움직이는 걸 볼 수 있다. 앞으로 문제를 풀 때는 뒤로 물러서서 바라볼 수 있는 안목도 길러야겠다.

재귀에 맞게 고친 풀이

#include <stdio.h>

void h(int n, int start, int mid, int to) {
    if(n == 1) {
        printf("%d %d\n", start, to);
        return;
    }

    h(n-1, start, to, mid);
    h(1, start, mid, to);
    h(n-1, mid, start, to);
}

int main() {
    int N;
    scanf("%d", &N);
    printf("%d\n", (1<<N)-1);
    h(N, 1, 2, 3);
}