2477: 참외밭

네르기·2022년 9월 10일

기하

알고리즘

목록 보기

69/76

어떤 문제인가?

직사각형 안에 직사각형이 들어간 모양이 주어졌을 때, 그 모양의 넓이를 구하는 문제.

시행착오 횟수

1번

1차 시도: WA

참외밭의 임의의 꼭짓점 에서 반시계 방향으로 돈다고 했었다. 그렇다면 그 시작점을 옮겨서 우리가 원하는 위치에 둔 후에 계산하면 어떨까?
이렇게 하기 위해서는 배열 원소들을 한 칸씩 옆으로 옮기는 shift 연산을 구현해야 한다. 나중에서야 알았는데 배열 swap을 재귀적으로 호출해서 구현하는 방법도 있었다. 링크는 후술한다.

참외밭의 전체 넓이를 구하는 건 쉽다. 이동 거리 및 방향이 주어지므로, 이것의 최댓값을 구하면 된다. 문제에서 주어진 도형을 만들기 위해서는 반드시 중복되는 2개의 방향이 있을 수 밖에 없다.
이게 무슨 소리일까? 아래의 그림을 보자.

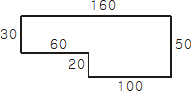
길이 60의 선분과 20의 선분이 만나는 지점에서 시작한다고 치자. 반시계 방향으로 돈다고 했으므로 시작점으로 돌아가기 위해서는 남 > 동 > 북 > 서 > 남 > 동 방향으로 이동해야 한다. 여기에서 기울임체로 표시된 방향들에 주목하자. 동, 남 방향이 2번 등장했다.

직사각형의 면적은 가로 * 세로로 구할 수 있다. 작은 직사각형의 면적 또한 그렇게 구할 수 있는데, 바로 그 작은 직사각형의 변들을 지나갈 때 그 변들의 길이를 곱하면 작은 직사각형의 넓이를 구할 수 있다. 우리는 어떤 방향으로 얼마나 갈 지 알기 때문에, 이걸 이용할 생각이다.

이 아이디어를 코드로 옮기면 다음과 같다.

include <stdio.h>
#define MAX(a, b) a > b ? a : b

void shift(int *arr) {
    int t = arr[5];
    for(int i = 5; i > 0; i--)
        arr[i] = arr[i-1];
    arr[0] = t;
}

int main() {
    int v = 0, h = 0, V[6], D[6], K;
    scanf("%d", &K);

    for(int i = 0; i < 6; i++) {
        scanf("%d %d", &D[i], &V[i]);

        if(D[i] == 1 || D[i] == 2) h = MAX(h, V[i]);
        else if(D[i] == 3 || D[i] == 4) v = MAX(v, V[i]);
    }

    for(int i = 0; i < 6; i++) {
        if(D[0] == D[2]) {
            printf("%d", K * (v * h - V[0] * V[1]));
            break;
        }
        shift(D);
        shift(V);
    }

    return 0;
}

2차 시도: AC

사실 위 코드는 한가지 치명적인 결함이 하나 있다. 무엇인지 알아챘는가?

문제에서 주어진 도형에 대해, 어떠한 임의의 꼭짓점을 시작점으로 잡든 그 전체 넓이는 절대로 변하지 않는다. 그렇지만 위 코드는 다음과 같이 시작점에 따라 달라지는 부분이 있다. 왜일까?

그림을 다시 보자. 일반적인 경우라면 위 코드는 다음과 같이 판단한다.

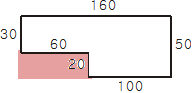
위처럼 올바른 부분을 제거하지만, 딱 단 한 상황에서만 엉뚱한 영역을 빼게 된다. 어디일까?

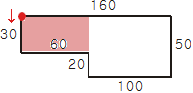
시작점을 한 칸씩 옮겨보면 알 수 있다. 앞서 말한 60 선분과 20 선분이 만나는 지점을 기준으로 방향을 이제는 숫자로 나타내어보자. 그리고 한 칸씩 시계 방향으로 옮겼을 때 어떤 일이 일어나는지 보자.

원본: 314231
1칸: 131423
2칸: 313142

코드와 대조했을 때 무엇이 문제인지 알아챘는가? 만약 2칸 움직인 것이 먼저 오게 된다면 해당 코드는 잘못된 결과를 내놓게 된다. 앞서 말한 '엉뚱한 영역'을 빼게 된다.
코드에서는 0번째 숫자와 2번째 방향이 같다면 계산을 하게끔 해놓았다. 그렇지만 위의 경우에 취약하므로, 이를 해결하기 위해서는 2칸 옮긴 지점에서의 방향 나열처럼 서로 같은 방향이 서로 인접하게 만든 후 넓이를 빼야 한다. 그렇다면 모든 경우에 대해서 올바른 답을 얻을 수 있다.

#include <stdio.h>
#define MAX(a, b) a > b ? a : b

void shift(int *arr) {
    int t = arr[5];
    for(int i = 5; i > 0; i--)
        arr[i] = arr[i-1];
    arr[0] = t;
}

int main() {
    int v = 0, h = 0, V[6], D[6], K;
    scanf("%d", &K);

    for(int i = 0; i < 6; i++) {
        scanf("%d %d", &D[i], &V[i]);

        if(D[i] == 1 || D[i] == 2) h = MAX(h, V[i]);
        else if(D[i] == 3 || D[i] == 4) v = MAX(v, V[i]);
    }

    for(int i = 0; i < 6; i++) {
        if(D[0] == D[2] && D[1] == D[3]) {
            printf("%d", K * (v * h - V[1] * V[2]));
            break;
        }
        shift(D);
        shift(V);
    }

    return 0;
}

다른 분들의 풀이

꼭짓점을 하나하나씩 지나가므로, 그 꼭짓점에서 만나는 두 변이 이루는 직사각형의 영역을 모두 더하면 원래 도형의 넓이와 전체 직사각형 2개의 넓이를 합한 것과 같게 된다. 그래서 그 2개의 직사각형을 제거하면 원래 도형 넓이를 얻을 수 있다. 이 풀이는 세심한 관찰이 필요하다.

#include <stdio.h>
int main(void)
{
    int k, i, x, max=0, sum=0;
    int a[7];
    scanf("%d", &k);
    for(i=0;i<6;i++)
        scanf("%d %d", &x, &a[i]);    //x는 필요없는 값
    a[6]=a[0];
    for(i=0;i<6;i++){
        sum+=a[i]*a[i+1];
        if(a[i]*a[i+1]>max)
            max=a[i]*a[i+1];
    }
    printf("%d\n", k*(sum-2*max));
    return 0;
}