조인의 원리
조인을 수행할 때는 조인의 원리를 기반으로 작업이 이루어진다. 조인은 기법을 달리하여 수행할 수 있는데 대표적인 조인 기법은 아래 세가지가 있다.
-
중첩 루프 조인 (Nested Loop, NL Join)
-
정렬 병합 조인 (Sort Merge Join)
-
해시 조인 (Hash Join)
중첩 루프 조인
-
프로그래밍에서 사용하는 중첩 for문과 유사한 방식으로 조인을 수행
-
반복문의 외부에 있는 테이블을 선행 테이블 또는 외부 테이블(Outer Table)이라 함
-
반복문 내부에 있는 테이블을 후행 테이블 또는 내부 테이블(Inner Table)이라고 함
-
선행 테이블의 조건을 만족하는 행을 추출하여 후행 테이블을 읽으면서 조인을 수행
-
결과 행의 수가 적은(처리 범위가 좁은) 테이블을 조인 순서 상 선행 테이블로 선택하는 것이 전체 일량을 줄일 수 있음
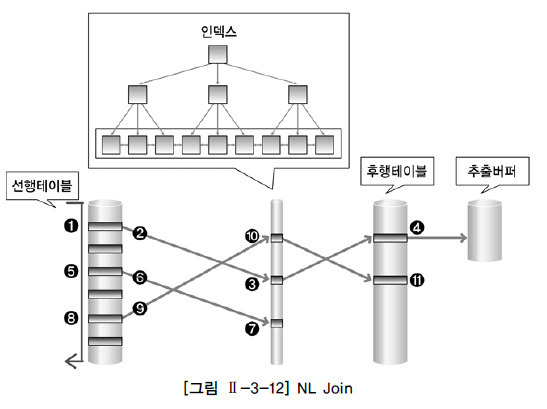
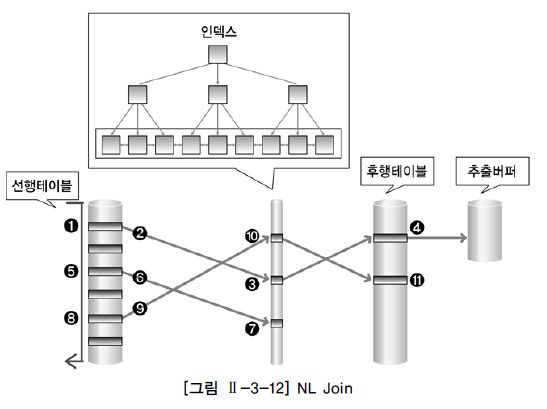
중첩 루프 조인의 동작 원리
-
선행 테이블에서 주어진 조건을 만족하는 행을 찾음
-
선행 테이블의 조인 키 값을 가지고 후행 테이블에서 조인 수행
-
선행 테이블의 조건을 만족하는 모든 행에 대해 1번 작업 반복 수행
정렬 병합 조인
-
정렬 병합 조인은 조인 칼럼을 기준으로 데이터를 정렬한 뒤 조인을 수행
-
정렬할 데이터가 많은 경우 임시 영역(디스크)을 사용하기 때문에 성능이 떨어질 수도 있음
-
대량의 조인 작업은 CPU 작업 위주로 처리하는 Hash Join이 성능상 유리
-
Hash Join과는 달리 동등 조인 뿐만 아니라 비동등 조인에 대해서 조인 작업 가능
-
조인 칼럼의 인덱스를 사용하지 않기 때문에 조인 칼럼의 인덱스가 존재하지 않을 경우에 사용가능
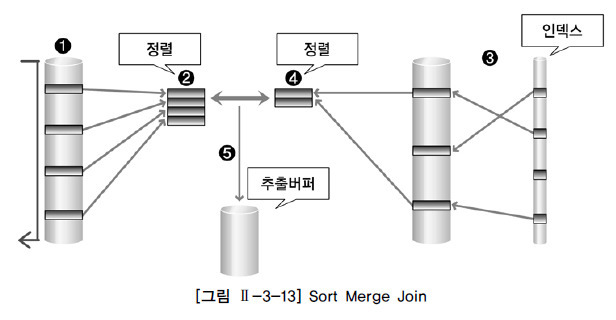
정렬 병합 조인의 동작 원리
-
선행 테이블에서 주어진 조건을 만족하는 행을 찾음
-
선행 테이블의 조인 키를 기준으로 정렬 작업을 수행
1~2번 작업을 선행 테이블의 조건을 만족하는 모든 행에 대해 반복 수행
-
후행 테이블에서 주어진 조건을 만족하는 행을 찾음
-
후행 테이블의 조인 키를 기준으로 정렬 작업을 수행
3~4번 작업을 후행 테이블의 조건을 만족하는 모든 행에 대해 반복 수행
- 정렬된 결과를 이용하여 조인을 수행하며 조인에 성공하면 추출버퍼에 넣음
해시 조인
-
Hash Join은 해슁 기법을 이용하여 조인을 수행
-
조인을 수행할 테이블의 조인 칼럼을 기준으로 해쉬 함수를 수행하여, 서로 동일한 해쉬 값을 갖는 것들 사이에서 실제 값이 같은지를 비교하면서 조인을 수행
-
Hash Join은 중첩 루프 조인의 랜덤 액세스 문제점과 정렬 병합 조인의 문제점인 정렬 작업의 부담을 해결
-
조인 칼럼의 인덱스를 사용하지 않기 때문에 조인 칼럼의 인덱스가 존재하지 않을 경우 사용 가능
-
동등(=) 조인에서만 사용 가능
-
해쉬 테이블을 메모리에 생성해야하고, 크기가 클 경우 임시 영역에 저장하기 때문에 결과 행의 수가 적은 테이블을 선행 테이블로 사용하는 것이 좋음
-
먼저 해쉬 테이블을 생성하는 빌드 단계(Build Input), 그리고 해쉬 테이블에 대해 해쉬 값의 존재 여부를 검사하는 프루브 단계(Prove Input)로 이루어짐
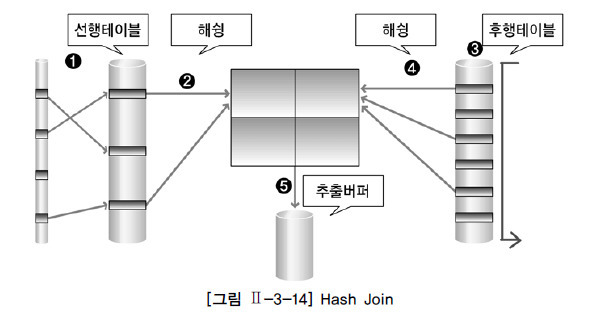
Hash Join의 동작 원리
-
선행 테이블에서 주어진 조건을 만족하는 행을 찾음
-
선행 테이블의 조인 키를 기준으로 해쉬 함수를 적용하여 해쉬 테이블을 생성
(조인 칼럼과 SELECT 절에서 필요로 하는 칼럼도 함께 저장됨)
1~2번 작업을 선행 테이블의 조건을 만족하는 모든 행에 대해 반복 수행
-
후행 테이블에서 주어진 조건을 만족하는 행을 찾음
-
후행 테이블의 조인키를 기준으로 해쉬 함수를 적용하여 해당 버킷을 찾음
(조인 키를 이용해서 실제 조인될 데이터를 찾음)
- 조인에 성공하면 추출버퍼에 넣음
3~5번 작업을 후행 테이블의 조건을 만족하는 모든 행에 대해서 반복 수행
