학습 목표
수치형 변수의 빈도수를 시각화하고 히스토그램과 분포에 대해 이해합니다.
핵심 키워드
히스토그램과 도수분포표
수치형 변수의 빈도수
왜도와 첨도
Point
히스토그램은 수치형 변수를 도수분포 형태로 구간화 하고 그 빈도수를 세어 시각화하기
히스토그램과는 다룹니다.
히스토그램을 통해 수치 데이터의 분포를 알 수 있습니다.
또, 히스토그램의 막대의 갯수(bins)를 몇 개로 나눠 그리는지에 따라 그래프의 모양이 달라집니다.
히스토그램의 모양을 통해 자료가 한쪽으로 치우쳐져 있는지 너무 뾰족한지 등을 보게 되는데 이런 수치를 왜도와 첨도라 부릅니다.
히스토그램과 분포
히스토그램(histogram)은 표로 되어 있는 도수 분포를 정보 그림으로 나타낸 것
도수 분포(度數分布, frequency distribution) 또는 빈도분포는 표본의 다양한 산출 분포를 보여주는 목록, 표, 그래프
표에 들어가는 각 항목은 특정 그룹이나 주기 안에 값이 발생한 빈도나 횟수를 포함하고 있으며 이러한 방식으로 표는 표본 값의 분포를 요약
# 수치형 변수 mpg의 unique 값 보기
df["mpg"].unique()
# hist()를 통해 전체 수치변수에 대한 히스토그램 그리기
_=df.hist(figsize=(10,8), bins=50)
비대칭도(왜도)
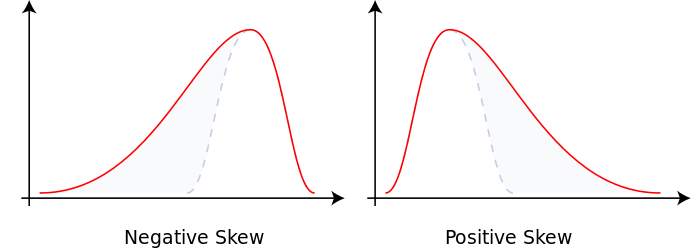
실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표로 왜도의 값은 양수나 음수가 될 수 있으며 정의되지 않을 수도 있음
왜도가 음수일 경우에는 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지며 중앙값을 포함한 자료가 오른쪽에 더 많이 분포하고 왜도가 양수일 때는 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 자료가 왼쪽에 더 많이 분포
평균과 중앙값이 같으면 왜도는 0
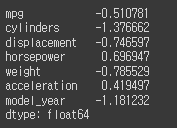
# skew를 통해 전체 수치변수에 대한 왜도 구하기
df.skew()
첨도
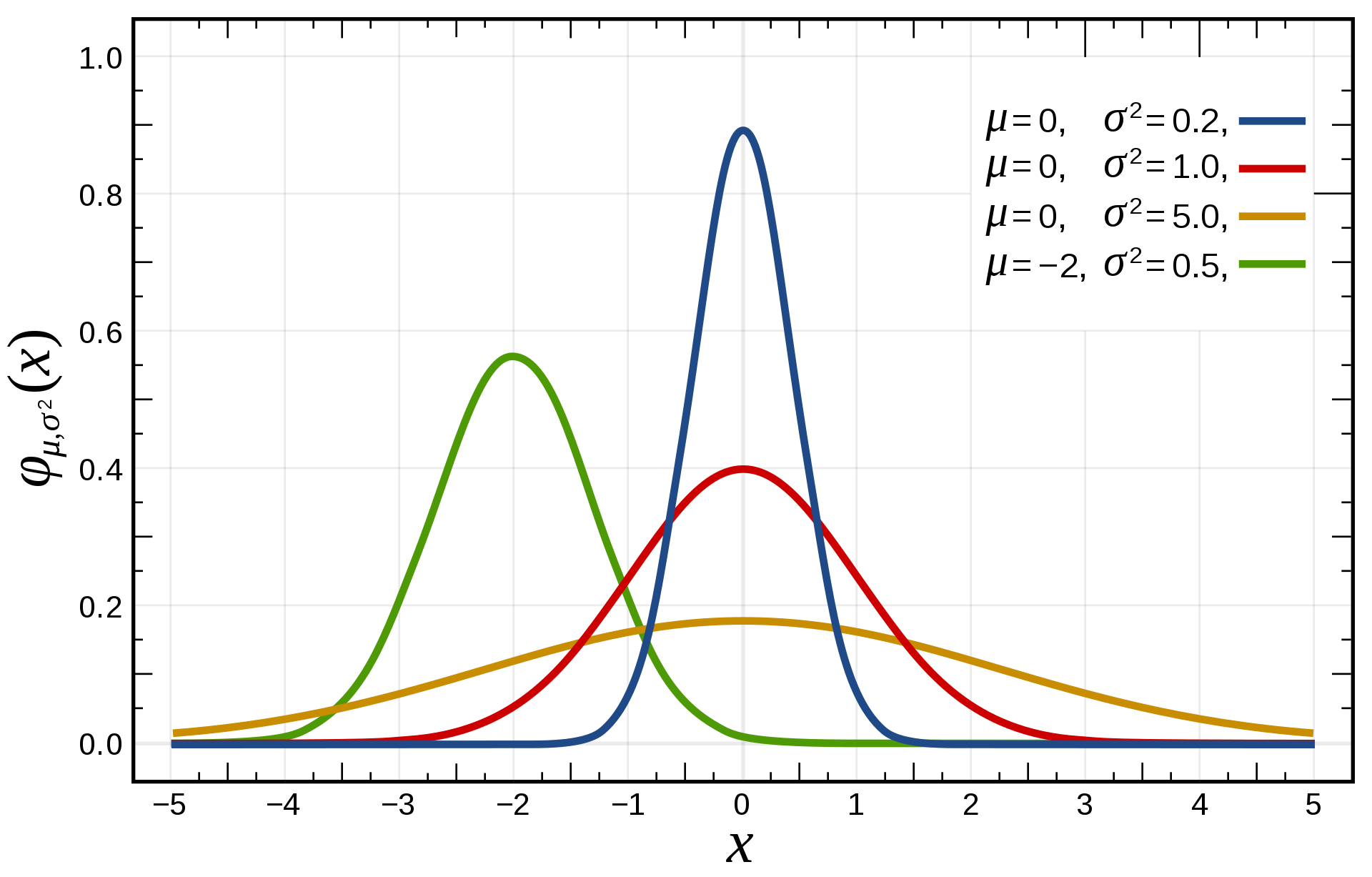
확률분포의 뾰족한 정도를 나타내는 척도로 관측치들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용합니다.
첨도값(K)이 3에 가까우면 산포도가 정규분포에 가까운데 3보다 작을 경우에는(K<3) 산포는 정규분포보다 더 뾰족한 분포(꼬리가 얇은 분포)이고 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 더 완만한 납작한 분포(꼬리가 두꺼운 분포)입니다.
# kurt를 통해 전체 수치변수에 대한 첨도 구하기
df.kurt()