딕셔너리와 집합

집합 이론

집합은 고유한 객체의 모음으로, 중복 항목을 제거하고 반드시 해시할 수 있어야 합니다. set은 해시 가능하지 않지만 frozenset는 해시 가능하므로, forzenset이 set에 들어갈 수 있다.

고유함을 보장하는 것 외에 집합형은 중위 연산자를 이용해서 기본적인 집합 연산을 구현하고, 이를 잘 활용하면 프로그램의 소스 코드 크기와 실행 시간을 줄일 수 있고, 루프나 조건절이 없어지기에 코드의 가독성이 높아진다.

#둘 다 집합형인 haystack 안에 들어 있는 needies 항목 수 구하기
found = len(needles & haystack)

#집합을 안 쓰기

found = 0
for n in needles:
	if n in haystack:
    	found += 1
        
#haystack 안에서 needles의 발생 횟수 수하기(set형 만들기)

found = len(set(needles) & set(haystack))

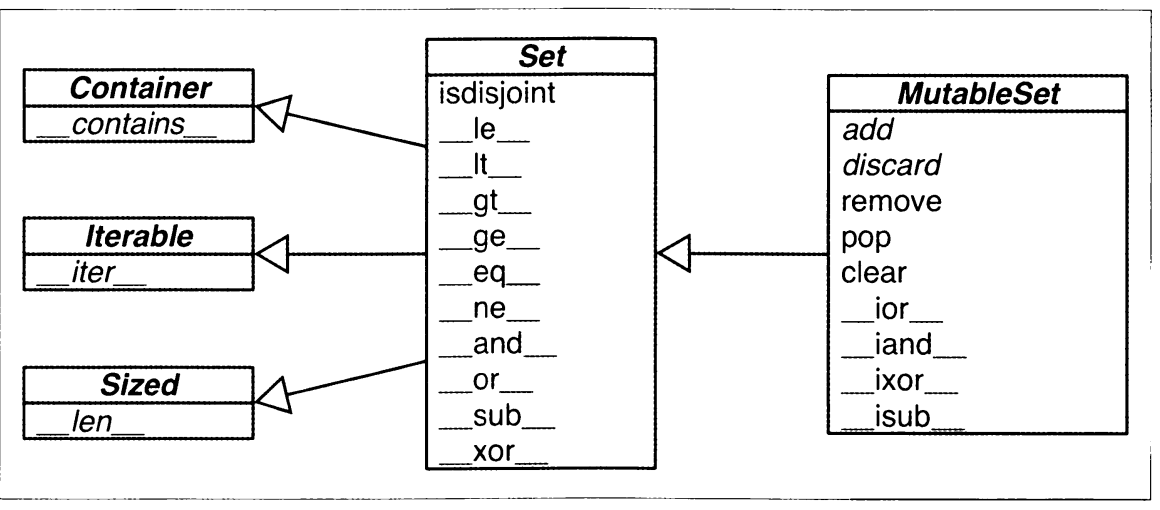
found = len(set(needles).intersection(haystack))

내부의 해시 테이블 덕분에 집합 안에 속해 있는지 여부를 아주 빨리 검색할 수 있는 것 외에도 set과 frozenset 내장 자료형은 새로운 집합을 생성하거나, set의 기존 항목을 변경하는 다양한 연산을 제공한다.

집합 리터럴

공집합은 리터럴로 표기할 수 없으므로, 반드시 set()으로 표기해야하고, 공집합을 생성할 때는 인수없이 생성자를 호출하는 set()구문을 사용해야 한다. 주의해야할 점은 {} 구문을 사용하면 빈 딕셔너리가 생성되므로 주의해야 한다.

"""
리터럴 집합 구문을 처리할 경우, 파이썬은 BUILD_SET이라는 특수 바이트코드를 실행한다.
"""

from dis import dis
dis('{1}') #1

   0 LOAD_CONST               0 (1)
   2 BUILD_SET                1
   4 RETURN_VALUE

dis('set([1])')

			  0 LOAD_NAME                0 (set)
              2 LOAD_CONST               0 (1)
              4 BUILD_LIST               1
              6 CALL_FUNCTION            1
              8 RETURN_VALUE

지능형 잡합

지능형 딕셔너리에서 설명한 dictcomp와 함께 추가되었다.

from unicodedata import name
{chr(i) for i in range(32,256) if 'SIGN' in name(chr(i),'')}

집합 연산

가변형과 불변형 집합에 사용할 수 있는 메서드로 상당 수는 연산자를 오버로딩하기 위한 특수 메서드입니다. 수학 집합 연산자를 파이썬의 해당 연산자나 메서드에 대응해서 설명하는 것으로, &=와 difference_update() 등 일부 연산자와 메서드는 대상 집합을 직접 변강한다.(frozenset에는 구현되어 있지 않다)