Density Estimation(밀도 추정)이란?
확률 밀도 추정이란? 관측된 데이터로부터 변수가 가질 수 있는 모든 값의 확률을 추정하는 것.
확률 밀도 추정 방법은 Parametric과 Non-parametric 두 가지 방법으로 구분할 수 있다.
1. Parametric
관측된 데이터를 바탕으로 관심 대상인 확률 변수가 특정 분포를 따른다는 가정 하에 확률밀도를 추정하는 방법.(데이터에 대한 확률분포를 미리 정하고, 그 확률 분포의 모수를 추정하는 방법)
- 첫번째, 관심 대상인 확률 변수의 분포를 우리가 이미 알고 있는 분포 중에서 하나를 가정
- 두번째, 관측된 데이터로부터 앞에서 정한 분포의 모수를 추정
이처럼 데이터로부터 모수를 구함으로써 분포를 추정하는 방법을 '모수 추정법'이라고 한다.
=> 가우시안 밀도 추정, 혼합 가우시안 밀도추정(GMM)
2. Non-Parametric
비모수 추정법은 특정 분포를 가정하지 않기 때문에 모수를 구하지 않고도 확률밀도를 추정할 수 있는 방법. (데이터로 확률밀도함수를 추정하려는 방법)
- 대표적인 방법으로, 히스토그램이 있다.
데이터로부터 히스토그램을 구한 후 정규화하여 확률 밀도 함수를 도출한다. 그러나, 히스토그램 기반 밀도 추정 방법은 아래와 같이 한계점이 존재한다.- 계급구간(bin)의 경계가 불연속적(discrete)
- 계급구간(bin)의 시작 위치에 따라 히스토그램(분포)가 달라짐
- 계급구간(bin)의 크기에 따라 히스토그램(분포)가 달라짐
- 고차원 데이터에 대해서는 메모리 문제 등으로 사용이 어려움
=> 커널 밀도 추정
reference : https://sungkee-book.tistory.com/2
1-1) Gaussian Density Estimation
데이터가 하나의 정규분포를 따른다고 가정하고 사용하는 방법론
<장점>
- 1) 데이터를 스케일링하는데 민감하지 않음
- 2) 식 자체가 주어져 있기 때문에 추가적인 분석이 가능
즉, p(X)를 미분을 하는 등 여러 방법을 사용해 최적을 임계값을 분석적으로 계산 가능
reference : https://jayhey.github.io/novelty%20detection/2017/11/02/Novelty_detection_Gaussian/
1-2) Mixture of Gaussain Density Estimation
하나의 가우시안 분포만으로 설명하게에 데이터가 더 복잡한 경우, 가우시안 혼합 모델을 이용하여 분포를 추정한다.
<특정 데이터가 4개의 혼합 가우시안 분포를 따른다고 가정한 케이스>
만약 1개의 가우시안 분포로 추정한다고 하면, 혼합 가우시안 분포보다 더 설명력이 낮은 분포가 그려질 것을 알 수 있다.
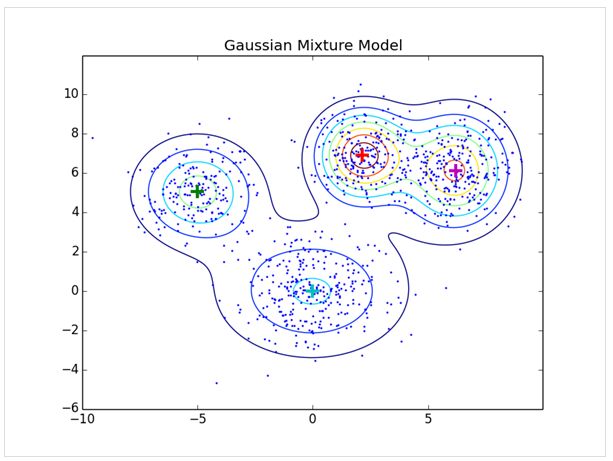
-
Gaussian Mixture Model(GMM) : K개의 서로 다른 Gaussian 분포의 가중합
=
= , : 각 가우시안 분포의 가중치, 임의의 샘플이 k번째 가우시안 분포(k번째 cluster)에 속할 확률 -
혼합 가우시안 분포의 특징
- 여러 개의 가우시안 분포로 확정
- 정규분포들의 선형 조합으로 만들어짐
- 단일 가우시안 분포보다 작은 bias를 가지고 있음. 그러나, 학습에 더 많은 데이터가 필요. -
혼합 가우시안 모델의 분포 추정 방법?
-> 단일 가우시안 분포는 convex하기 때문에 하기 때문에 최대가능도 추정법을 이용해 최적값을 찾아낼 수 있었다. 그러나 혼합 가우시안 모델은 convex하지 않아 정해진 최적값을 한 번에 찾을 수 없기 때문에 직접적으로 MLE를 적용하긴 어렵고, 휴리스틱 기법들로 풀어나가야 한다.
reference: https://jayhey.github.io/novelty%20detection/2017/11/03/Novelty_detection_MOG/
EM algorithm
- 주어진 데이터 : 훈련집합 , 가우시안 개수 k(사용자가 설정한다고 가정)
- 추정해야 할 매개변수 집합 :
[가우시안 혼합을 위한 EM 알고리즘]
input : 훈련집합 , 가우시안 개수 k
output : 최적의 가우시한 혼합계수
- 를 초기화 (난수로 설정하고 출발)
- While(!멈춤조건)
- 를 이용하여 소속확률 행렬 Z를 추정 (E-step)
- 를 이용하여 를 추정 (M-step)
: k*n 크기의 행렬 ( : 샘플 가 j번째 가우시안에 속할 확률)
ex) k=2라 했을 때, = 은 이 첫 번째 가우시안에 속할 확률은 0.07, 두 번째 가우시안에 속할 확률은 0.93이라는 사실을 뜻함.
- 2개의 가우시안이 자신에 속하는 샘플이 어느 것인지 알면, 소속된 샘플을 이용하여 평균과 공분산 행렬을 다시 추정하여 자신을 개선할 수 있다.
- (E-step) 가우시안이 자신의 매개변수()를 개선하면, 개선된 가우시안으로 샘플의 소속정보()를 개선할 수 있다.
- (M-step)개선된 소속정보()는 가우시안()을 더 정확하게 개선한다.
- 이처럼 두 과정을 번갈아 가며 반복함으로써 수렴점에 도달하는 방법을 EM 알고리즘이라 한다.
reference : 오일석의 기계학습
2-1) Kernel density estimation
-
Kernel Function : 커널함수란 다음 3가지 조건을 모두 만족하는 함수를 의미
(1)
(2) for all values of u.
(3) Non-negative -
Kernel Density Estimation이란?
커널 함수와 데이터를 바탕으로 연속성 있는 확률 밀도 함수를 추정하는 것.
- 관측된 데이터마다 해당 데이터를 중심으로 하는 커널함수를 생성한 후, 해당 커널 함수를 모두 더하고 데이터 개수로 나누면 KDE로 도출된 확률 밀도함수를 구할 수 있다.
= =- h: 대역폭(bandwidth)를 결정하는 파라미터, 대역폭은 확률밀도함수를 smoothing하는 역할을함 ( 대역폭 값이 작을수록 KDE 모양은 뾰족하고, 클수록 완만한 형태를 띠게 됨)
ex) 다음과 같이 6개의 데이터를 바탕으로 밀도를 추정한다고 하자.
= -2.1, = -1.3, = -0.4, = 1.9, =5.1, = 6.2
커널함수는 정규분포로, h = 1로 정한다.
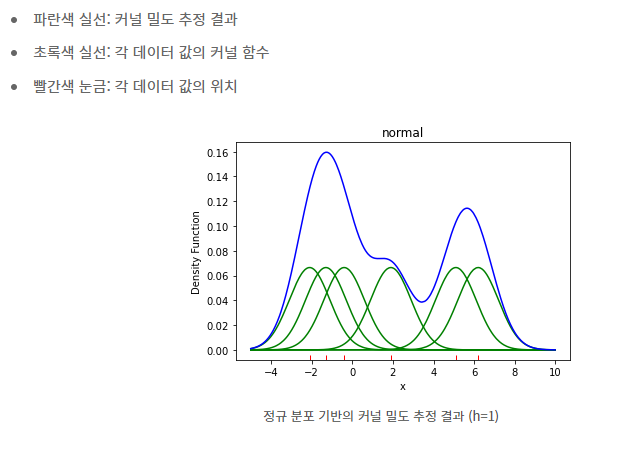
- h(smoothing parameter) 변화에 따른 KDE 결과
아래는 동일한 데이터와 커널함수(정규분포)일 때, h값에 따른 KDE 결과를 나타낸다.
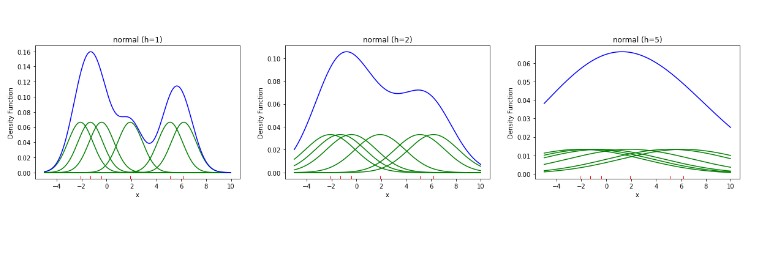
reference: https://sungkee-book.tistory.com/2