[XAI] Shapley Value

해당 포스팅에 사용된 자료의 출처는 고려대학교 산업경영공학부 김성범교수님의 Youtube 임을 밝힙니다.

Shapley Value

특정변수와 관련된 모든 변수 조합들을 입력시켰을 때 나온 결과값과 비교를 하면서 변수의 기여도를 계산하는 방식.

Example) 변수 하나(X1)에 대한 Shapley value 구하는 방법.

X1 변수를 예측에 사용하는지 여부에 따른 예측값 비교.

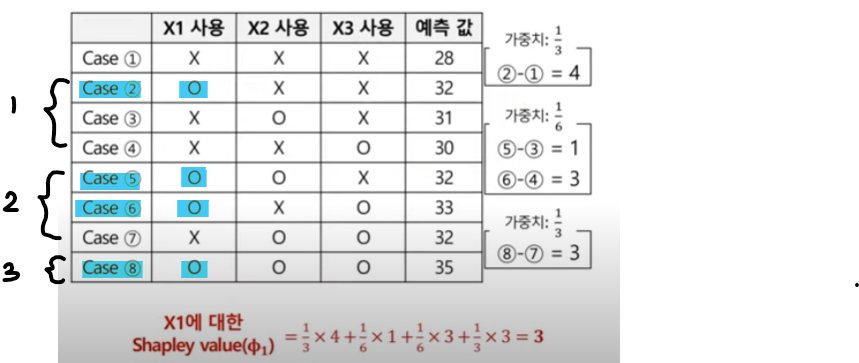
1. 변수 1개만 사용하는 경우 (case 2,3,4)
- X1 여부에 따른 예측값 차이 : 4
- 총 3가지 case 중 (case2,3,4) X1 제거가 가능한 경우는 1가지(case2)이므로 가중치는 $\frac{1}{3}$.
2. 변수 2개를 사용하는 경우(case 5,6,7)
- X1 여부에 따른 예측값 차이: 1, 3
- case 5의 경우, 변수를 1개 제거할 수 있는 case는 X1을 제거한 경우 or X2를 제거한 경우 총 2가지가 나옴. case 6과 7도 마찬가지이므로 변수를 제거할 수 있는 경우의 수는 총 6가지가 된다. 여기서 우리가 구하고자 하는 X1을 제거한 경우는 case5에서 1가지이므로 가중치는 $\frac{1}{6}$.
- case 6의 경우도 마찬가지로 가중치는 $\frac{1}{6}$.
3. 변수 3개를 사용하는 경우(case 8)
- X1 여부에 따른 예측값 차이: 3
- 변수를 1개 제거할 수 있는 경우는 총 3가지(X1 or X2 or X3)이고, 이 중 X1을 제거한 경우는 1가지이므로 가중치는 $\frac{1}{3}$.

$\therefore$ X1에 대한 Shapley Value는 가중치 x case별 예측값의 차이로 구할수 있다.

$\phi_{x_1}$ = $(4 \cdot \frac{1}{3}) + (1 \cdot \frac{1}{6} ) + ( 3 \cdot \frac{1}{6}) + (3 \cdot \frac{1}{3}) = 3$

---

일반화

$\phi_i$ = $\sum_{S \in F/\{i\}}\frac{|S|!(|F|-|S|-1)!}{|F|!}(f(S\cup\{i\})-f(S))$

• $\phi_{i}$ : 특정 변수의 Shapley value.
• F : 전체 변수의 부분 집합
• i : 관심 있는 변수 집합
• S : 관심 변수가 제외된 변수의 부분집합.

---

Shapley Value 해석

• SHAP value : 각 관측치별 중요도를 구함.
• mean(|SHAP value|) : 각 관측치별 중요도를 평균낸 값.

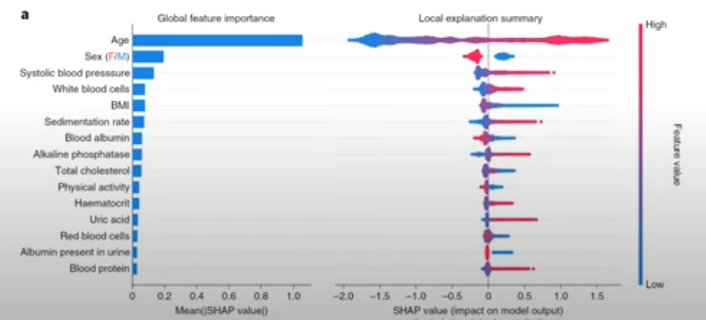
• 왼쪽 그림은 전반적인 변수 중요도를 의미.

• 오른쪽 그림 위주로 설명.
  - X축 : SHAP value 값, 오른쪽으로 갈수록 해당 변수가 예측값(여기서 사망률)에 큰 기여를 했음을 의미.
  - Y축 : 각 변수마다 큰 값일수록 붉은색, 작은 값일수록 파란색으로 표시.

  ex) 나이가 많으면, 사망률에 대한 기여도가 크다.
      남성(파란색)이 여성보다 사망률에 대한 기여도가 크다.
      BMI가 낮을수록, 사망률에 대한 기여도가 크다. 

---

https://www.youtube.com/watch?v=f2XqxOny3NA&t=685s
https://techblog-history-younghunjo1.tistory.com/200