코딩테스트

보글 게임 문제의 분할 우리가 해결해야 할 문제는

사다리 조작우리가 해결해야 할 문제는 'i번 세로선의 결과는 i번이 나오도록 하기 위해 추가해야하는 가로선의 개수는 몇 개 인가?' 입니다. 이 문제는 '현재 사다리의 상태에서 $x$개의 가로선을 추가하면 i번 세로선의 결과는 i번이 나오는 사다리가 되는가?'를 풀 수

소풍여기서 해결해야 할 문제는 '아직 짝을 찾지 못한 학생들의 명단이 주어질 때 친구끼리 둘씩 짝짓는 경우의 수를 계산하라'입니다. 경우의 수를 반환하는 int countPairings(boolean taken\[10]) 함수를 만들면 됩니다. 이 함수를 호출하면 짝을

시계 맞추기이 문제는 그냥 풀려고 하면 꽤 어렵습니다. 하지만 문제의 특성을 이용해 적절히 단순화하면 완전 탐색으로 해결할 수 있습니다.이 문제에서 처음 깨달아야 할 것은 스위치를 누르는 순서는 중요하지 않다는 것입니다. 스위치를 누르는 순서를 바꿔도 결과는 같습니다.

치킨 배달우리가 해결해야 할 문제는 '치킨집의 개수가 $M$개까지 줄어들었을 때 도시의 치킨 거리가 가장 작은 경우의 도시의 치킨 거리를 구하라'입니다. 최적화 문제입니다. 만들 수 있는 치킨집의 모든 조합을 만들어 보고 최솟값을 구하면 됩니다. 문제를 '현재 도시의

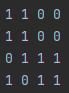
쿼드 트리 뒤집기이 문제를 풀 수 있는 가장 무식한 방법은 주어진 그림의 쿼드 트리 압축을 풀어서 실제 이미지를 얻고 상하 반전한 뒤 다시 쿼드 트리 압축하는 것입니다. 물론 그림의 크기 제한이 매우 크기 때문에 무식한 방법으로 풀 수 없습니다. 이런 경우 대개 우리가

울타리 잘라내기

가장 가까운 두 점모든 점끼리 거리를 구해서 비교하면 풀 수 있습니다. 하지만 시간 복잡도가 $O(n^2)$이므로 절대 시간 안에 해결할 수 없습니다.분할 정복 알고리즘으로 문제를 해결하려면 세 가지 구성 요소를 만들어야 합니다.첫 번째 구성 요소를 만들기 위해선 무엇

외발 뛰기우선 무식하게 푸는 방법을 생각해 봅시다. 동적 계획법 알고리즘을 만드는 첫 단계는 해당 문제를 재귀적으로 해결하는 완전 탐색 알고리즘을 만드는 것입니다. 완전 탐색 알고리즘은 맨 왼쪽 윗 칸에서 시작하는 모든 경로를 하나씩 만들어 보면서 마지막 칸에 도달할

와일드카드이 문제는 \*을 해결하는 것이 어렵습니다. 알파벳이나 ?는 한글자씩 넘어가며 검사하면 되지만 \*에 해당되는 글자는 몇 글자인지 모르기 때문에 모든 경우의 수를 계산해봐야 합니다. 따라서 일단 글자를 하나씩 맞춰보고 \*를 만나거나 둘 중 한 문자열이 끝날

삼각형 위의 최대 경로우선 무식하게 푸는 방법을 생각해보겠습니다. 모든 경로를 다 확인하는 것이므로 한번 내려갈 때 2가지 경우의 수가 있으므로 $n$개의 가로줄이 있을 때 가능한 경로의 수는 $2^{n - 1}$입니다. $n$이 100이라면 절대 해결할 수 없는 수치

최대 증가 부분 수열우선 단순한 완전 탐색 알고리즘으로 구현해 봅시다. 완전 탐색 알고리즘으로 구현하려면 부분 문제를 정의해야 합니다. 이 문제에서 부분 문제는 수열의 특정 위치에서 시작하는 최대 증가 부분 수열을 찾는 것입니다. 따라서 int lis(int start

합친 LIS두 수열에서 증가 부분 수열을 하나 고른 뒤 두 증가 부분 수열을 증가 부분 수열이 되도록 합쳤을 때 가장 길이가 긴 증가 수열의 길이를 구하는 문제입니다. 딱 보고 드는 무식하게 푸는 방법은 이전 문제에서 봤듯이 한 수열의 증가 부분 수열은 시작 위치에 따

원주율 외우기숫자를 세 자리에서 다섯 자리까지 끊어 읽을 수 있습니다. 1111222인 숫자는 {1111, 222} 혹은 {111, 1222}로 나눌 수 있습니다. 최대 만 자리 숫자까지 입력 받으므로 최소 $2^{10000/7}=2^{1428}$ 가지 경우의 난이도의

타일링 방법의 수 세기경우의 수를 세는 문제입니다. 경우의 수 계산하기 레시피를 참고해서 풀면 좋습니다.우선 완전 탐색을 이용해 모든 답을 만들면서 개수를 세어 보는 함수를 작성한 뒤, 메모이제이션을 이용해 동적 계획법 알고리즘으로 바꿔 봅시다. 재귀 호출을 할 때 부

삼각형 위의 최대 경로 개수 세기이전에 풀었던 삼각형 위의 최대 경로 찾기 문제를 돌이켜 봅시다. 삼각형 위의 최대 경로 찾기 문제에서는 각 위치에서 맨 밑으로 내려갔을 때 최대한 얻을 수 있는 값을 구했습니다. 우리가 지금 구하고 싶은 것은 최대한 얻을 수 있도록 하

가장 긴 증가하는 부분 수열 4이 문제는 최적화 문제의 답을 계산하는 문제입니다. 동적 계획법 테크닉을 보면 쉽게 해결할 수 있습니다.최대 증가 부분 수열 문제에서 사용했던 알고리즘에 몇가지만 더 추가하면 됩니다. 이전 문제에서 사용했던 $lis()$ 함수에서 매 부분

여행 짐 싸기물건의 모든 조합을 하나한 검사하고 이들 중 최적의 조합을 찾아내는 완전 탐색 알고리즘을 작성해 봅시다. 각 물건에 대해 가져가거나 말거나 두 가지의 선택이 있으므로 전체 $2^n$개의 조합이 있습니다. 다음과 같은 부분 문제를 얻을 수 있습니다.$pack

출전 순서 정하기$n$명의 선수들의 순서를 정하는 방법은 $n!$개 있습니다. $n!$은 숫자가 조금만 커져도 계산량이 매우 많아집니다.한국팀의 출전 순서를 맨 앞에서부터 한 명씩 정해가기로 하면, 각 선수를 지금까지 순서에 추가했는지를 나타내는 boolean값 배열만

도시락 데우기우리가 해결해야 하는 것을 정의해 봅시다. 한 도시락을 먹을 때까지 걸리는 시간은 지금까지 데운 모든 도시락을 데우는 시간의 합에 이 도시락을 먹는데 걸리는 시간을 더한 것입니다. 우리는 그중 가장 큰 값(제일 늦게 다 먹는 도시락)을 최소화하려고 합니다.

졸업 학기이 문제를 푸는 알고리즘 자체는 전형적인 지수 시간 동적 계획법입니다. 동적 계획법 알고리즘을 만들기 위해서는 우선 완전 탐색 알고리즘을 설계하고 이것을 메모이제이션으로 최적화해야 합니다. 그리고 완전 탐색으로 문제를 풀기 위해서는 문제를 여러 조각으로 나눈

조세푸스문제를 이해한다면 연결 리스트로 풀어야 한다는 생각이 딱 들것입니다. 리스트의 중간 요소를 하나씩 제거하는 연산을 효율적으로 처리할 수 있는 자료구조가 연결 리스트이기 때문입니다.반복문이 하나이므로 시간 복잡도는 $O(n)$입니다. n의 최댓값은 1000이기 때

짝이 맞지 않는 괄호매우 직관적으로 스택을 써야 한다는 것을 알 수 있습니다. 약간 생각해야할 것은 예외 처리입니다. 스택이 비어있거나 모든 식을 다 검사하고 여는 괄호가 스택에 남아있는 경우를 처리해줘야 합니다.

외계 신호 분석우선 간단한 완전 탐색 알고리즘으로 생각해 보겠습니다. 모든 신호를 만들고 앞에서부터 차례차례 구간합을 구해서 K를 만들 수 있는지 검사하고, K를 넘어가면 다음 신호부터 구간합을 검사하면 됩니다. 아래는 이 아이디어를 구현한 코드입니다.시간 복잡도를 계

수 찾기처음에 배열에서 수를 찾는 문제이므로 이분 탐색으로 해야 겠다 싶어서 N의 최댓값을 봤더니 100,000이었습니다. 원래 이분 탐색의 시간 복잡도는 $O(\\log N)$이지만 잠깐 착각해서 $O(N\\log N)$으로 생각하고 문제를 풀었습니다. 그래서 이분

트리 순회 순서 변경이 문제는 얼핏 보기엔 까다로워 보이지만 재귀 호출을 이용하면 아주 간단하게 구현할 수 있습니다. 다음과 같은 형태의 $printPostOrder()$ 함수를 정의해봅시다.$printPostOrder(preOrder\[], inOrder\[])$=트

이중 우선순위 큐이 문제를 딱 보자마자 정렬 기준이 다른 우선순위 큐를 이용해서 풀면 될 것이라고 생각했다. 하나는 최대힙, 하나는 최소힙으로 하고 숫자를 넣을 때마다 size를 1 올리고 뺄 때마다 size를 1 빼면 두 개의 힙에 몇 개가 남든지 size로 판단하고

DSLR딱 봐도 너비 우선 탐색으로 풀어야겠다고 생각했습니다. 이 문제의 관건은 DSLR 각 연산을 어떻게 처리하냐 입니다. 처음엔 L연산과 R연산을 할 때 4자리 수가 아닌 숫자들을 처리하기 위해 처음에 4자리 수로 맞추고 시작하면 편할 것 같아서 StringBuil

테트로미노처음엔 모든 테트로미노의 모양을 배열에 저장해서 하나하나 비교하는 식으로 하려 했습니다. 회전과 대칭 모두 검사해야 하므로 배열을 만드는 것이 쉽지 않았습니다. 실수할 확률도 매우 높았습니다. 역시나 실수해서 이런 식으로 푸는 것은 매우 비효율적이고 도움이 안