트리

지식 저장소·2021년 12월 23일

문제해결기법

목록 보기

21/21

도입

우리는 문제를 해결하기 위해 수학의 '집합' 개념을 이용할 수 있습니다. 집합은 여러 가지 방식으로 표현할 수 있습니다.
집합에 대한 대표적인 연산으로 검색, 삽입, 삭제가 있습니다. 만약 집합을 배열로 구현한다면 검색은 $O(n)$ , 삽입은 $O(1)$ , 삭제는 $O(n)$ 이 걸립니다.
트리는 삽입은 $O(\log n)$ 으로 더 오래 걸리지만 나머지가 $O(\log n)$ 으로 감소합니다. $O(n)$ 에 비해 $O(\log n)$ 은 훨씬 작으므로 집합을 배열보단 트리로 구현하는 것이 대부분 더 효율적입니다.

트리 관련 용어

루트
트리의 가장 윗부분에 위치하는 노드를 루트라고 합니다. 하나의 트리에는 하나의 루트가 있습니다.

리프
트리의 가장 아랫부분에 위치하는 노드를 리프라고 합니다. 이때 '가장 아래에 위치한다'라는 말은 물리적으로 가장 아랫부분에 위치한다는 의미가 아니라 더 이상 뻗어나갈 수 없는 마지막에 노드가 위치한다는 의미입니다. 즉, 자식이 없는 노드를 말합니다.

안쪽 노드
루트를 포함하여 리프를 제외한 노드를 안쪽 노드라고 합니다.

자식
어떤 노드로부터 가지로 연결된 아래쪽 노드를 자식이라고 합니다.

부모
어떤 노드에서 가지로 연결된 위쪽 노드를 부모라고 합니다. 노드는 1개의 부모를 가집니다.

형제
같은 부모를 가지는 노드를 형제라고 합니다.

조상
어떤 노드에서 가지로 연결된 위쪽 노드 모드를 조상이라고 합니다.

자손
어떤 노드에서 가지로 연결된 아래쪽 노드 모두를 자손이라고 합니다.

레벨
루트로부터 얼마나 떨어져 있는지에 대한 값을 레벨이라고 합니다. 루트의 레벨은 0이고 루트로부터 가지가 하나씩 아래로 뻗어나갈 때마다 레벨이 1씩 늘어납니다.

차수
노드가 갖는 자식의 수를 차수라고 합니다.

높이
루트로부터 가장 멀리 떨어진 리프까지의 거리를 높이라고 합니다.

서브 트리
트리 안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리를 서브 트리라고 합니다.

널 트리
노드, 가지가 없는 트리를 널 트리라고 합니다.

순서 트리와 무순서 트리
형제 노드의 순서가 있는지 없는지에 따라 트리를 두 종류로 분류합니다. 형제 노드의 순서를 따지면 순서 트리, 따지지 않으면 무순서 트리라고 합니다.

전위 순회
노드 방문 -> 왼쪽 자식 -> 오른쪽 자식 순서로 탐색합니다.

중위 순회
왼쪽 자식 -> 노드 방문 -> 오른쪽 자식 순서로 탐색합니다.

후위 순회
왼쪽 자식 -> 오른쪽 자식 -> 노드 방문 순서로 탐색합니다.

이진검색트리

이진검색트리는 이진트리가 다음 조건을 만족하면 됩니다.

어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 모든 노드 N의 키 값보다 작아야 합니다.

오른쪽 서브 트리 노드의 키 값은 노드 N의 기 값보다 커야 합니다.

같은 키 값을 갖는 노드는 없습니다.

이진검색트리를 중위 순회하면 키 값의 오름차순으로 노드를 얻을 수 있습니다.

이진검색트리 만들기

노드 클래스 Node<K, V>

이진검색트리의 개별 노드를 나타내는 것이 클래스 Node<K,V>이며, 이는 다음과 같이 4개의 필드로 구성됩니다.

key $\space\space\space\cdots$ 키 값

data $\space\cdots$ 데이터

left $\space\space\space\cdots$ 왼쪽 자식 노드에 대한 참조(왼쪽 포인터라고 부릅니다.)

right $\space\cdots$ 오른쪽 자식 노드에 대한 참조(오른쪽 포인터라고 부릅니다.)

다음 그림은 노드의 이미지를 나타낸 것입니다.

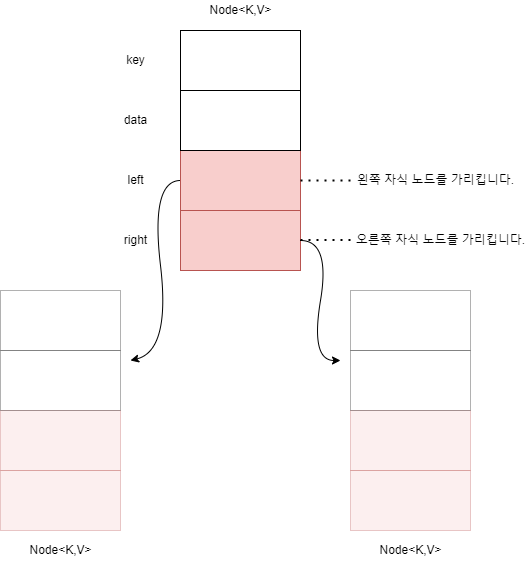
다음은 노드를 구현한 코드입니다. 쉬우므로 더 설명하지 않겠습니다.

public class BinTree<K, V> {
    // 노드
    static class Node<K, V> {
        private K key;                  // 키 값
        private V data;                 // 데이터
        private Node<K, V> left;        // 왼쪽 자식 노드
        private Node<K, V> right;       // 오른쪽 자식 노드
        
        // 생성자
        Node(K key, V data, Node<K, V> left, Node<K, V> right) {
            this.key = key;
            this.data = data;
            this.left = left;
            this.right = right;
        }
        
        // 키 값을 반환
        K getKey() {
            return key;
        }
        
        // 데이터를 반환
        V getValue() {
            return data;
        }
        
        // 데이터를 출력
        void print() {
            System.out.println(data);
        }
    }
        
    private Node<K, V> root;                            // 루트
    private Comparator<? super K> comparator = null;    // 비교자
}

이진검색트리 클래스 BinTree<K, V>

이진검색트리 클래스 BinTree<K, V>는 2개의 필드로 구성됩니다.

root $\space\space\space\cdots$ 루트에 대한 참조를 보존 $\cdot$ 유지하는 필드입니다.

comparator $\space\cdots$ 키 값의 대소 관계를 비교하는 비교자입니다.

생성자

클래스 BinTree<K, V>는 2개의 생성자가 있습니다. 둘 다 비어 있는 이진검색트리를 생성합니다.

    // 생성자: 자연 순서에 따라 키 값을 비교
    public BinTree() {
        root = null;
    }

    // 생성자: 비교자로 키 값을 비교
    public BinTree(Comparator<? super K> c) {
        this();
        comparator = c;
    }

두 키 값을 비교하는 comp 메서드

2개의 키 값을 비교하는 메서드입니다. 검색 $\cdot$ 삽입 $\cdot$ 삭제의 각 메소드에서 호출하는 비공개 메서드입니다.

// 두 키 값을 비교
private int comp(K key1, K key2) {
    return (comparator == null) ? ((Comparable<K>) key1).compareTo(key2) : comparator.compare(key1, key2);
}

이 메서드는 두 키 값 key1과 key2를 비교하여 아래 값을 반환합니다.

key1 > key2면 양수

key1 < key2면 음수

key1 == key2면 0

이진검색트리에 비교자 comparator가 설정되어 있는지 그렇지 않은지에 따라 2개의 키 값을 비교하는 방법이 다릅니다.

비교자가 comparator가 null인 경우
key1을 Comparable<K> 인터페이스형으로 형변환하고 compareTo 메서드를 호출하여 key2와 비교합니다.

비교자 comparator가 null이 아닌 경우
설정된 비교자 comparator의 compare 메서드를 호출하여 두 키 값 key1, key2를 비교합니다.

키 값으로 검색하는 search 메서드

아래 그림은 이진검색 트리의 검색 과정 중 한 예입니다.

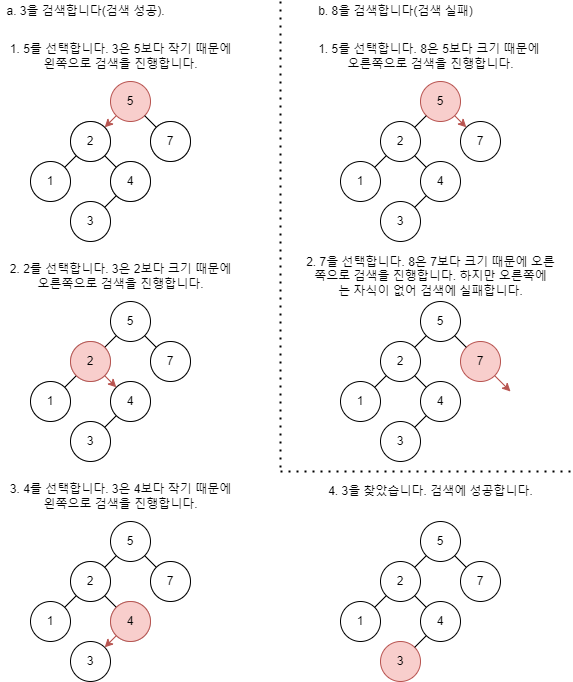
이진검색트리에서 원하는 값을 찾으려면 이런 방법으로 루트부터 시작해 현재 선택한 노드의 키 값과 목표하는 값을 비교하면서 왼쪽, 오른쪽으로 검색을 진행하면 됩니다. 알고리즘은 다음과 같습니다.

루트부터 선택하여 검색을 진행합니다. 여기서 선택하는 노드를 p라고 합니다.

p가 널이면 검색에 실패합니다.

검색하는 값 key와 선택한 노드 p의 키 값을 비교하여

값이 같으면 검색에 성공(검색 종료)합니다.

key가 작으면 선택한 노드에 왼쪽 자식 노드를 대입합니다(왼쪽으로 검색 진행).

key가 크면 선택한 노드에 오른쪽 자식 노드를 대입합니다(오른쪽으로 검색 진행).

2번 과정으로 되돌아갑니다.

search 메서드는 이 알고리즘을 바탕으로 이진검색트리에서 노드를 검색합니다.

    // 키에 의한 검색
    public V search(K key) {
        Node<K,V> p = root;                         // 루트에 주목
        
        while (true) {
            if (p == null)                          // 더 이상 진행하지 않으면
                return null;                        // 검색 실패
            int cond = comp(key, p.getKey());       // key와 노드 p의 키를 비교
            if (cond == 0)                          // 같으면
                return p.getValue();                // 검색 성공
            else if (cond < 0)                      // key 쪽이 작으면
                p = p.left;                         // 왼쪽 서브 트리에서 검색
            else                                    // key 쪽이 크면
                p = p.right;                        // 오른쪽 서브 트리에서 검색
        }
    }

키 값이 key인 노드를 검색하고 검색에 성공하면 그 노드의 데이터에 대한 참조를 반환합니다.

노드를 삽입하는 add 메서드

노드를 삽입할 때 주의해야 할 점은 노드를 삽입한 다음에 트리의 형태가 이진검색트리의 조건을 유지해야 한다는 점입니다. 따라서 노드를 삽입할 때는 알맞은 위치에 삽입해야 합니다. 이때 삽입할 노드의 키와 같은 값을 가지는 노드가 이미 있다면 노드를 삽입해서는 안 됩니다.
아래 그림을 보면 좀 더 자세히 알 수 있습니다.

node를 루트로 하는 서브 트리에 대해 키 값이 key인 데이터를 삽입하는 알고리즘은 다음과 같습니다(node가 널이 아닌 경우입니다).

루트를 선택합니다. 여기서 선택하는 노드를 node로 합니다.

삽입할 키 key와 선택 노드 node의 키 값을 비교합니다. 값이 같다면 삽입에 실패합니다(종료).

값이 같지 않은 경우 key 값이 삽입할 값보다 작으면
왼쪽 자식 노드가 없는 경우에는(a) 노드를 삽입합니다(종료).
왼쪽 자식 노드가 있는 경우에는 선택한 노드를 왼쪽 자식 노드로 옮깁니다.

key 값이 삽입할 값보다 크면
오른쪽 자식 노드가 없는 경우에는(b) 노드를 삽입합니다(종료).
오른쪽 자식 노드가 있는 경우에는 선택한 노드를 오른쪽 자식 노드로 옮깁니다.

2로 되돌아갑니다.

add 메서드는 이 알고리즘을 바탕으로 노드를 삽입합니다. 삽입하는 노드의 키 값은 key이고 데이터는 data입니다.

    // node를 루트로 하는 서브 트리에 노드<K,V>를 삽입
    private void addNode(Node<K,V> node, K key, V data) {
        int cond = comp(key, node.getKey());
        if (cond == 0)
            return;                                     // key가 이진검색트리에 이미 있음
        else if (cond < 0) {
            if (node.left == null)
                node.left = new Node<K,V>(key, data, null, null);
            else
                addNode(node.left, key, data);          // 왼쪽 서브 트리에 주목
        } else {
            if (node.right == null)
                node.right = new Node<K,V>(key, data, null, null);
            else
                addNode(node.right, key, data);         // 오른쪽 서브 트리에 주목
        }
    }
    
    // 노드를 삽입
    public void add(K key, V data) {
        if (root == null)
            root = new Node<K,V>(key, data, null, null);
        else
            addNode(root, key, data);
    }

노드를 삭제하는 remove 메서드

노드를 삭제하는 과정은 삽입하는 과정보다 복잡합니다. 노드를 삭제할 때는 '세 가지 서로 다른 상황'에 놓이기 때문입니다. 따라서 각각의 상황에 알맞은 처리를 해야 합니다.

$\color{white} \colorbox{brown}{A}$ 자식 노드가 없는 노드를 삭제하는 경우

이 과정을 간단히 정리하면 다음과 같습니다.

삭제할 노드가 부모 노드의 왼쪽 자식이면 부모의 왼쪽 포인터를 null로 합니다.

삭제할 노드가 부모 노드의 오른쪽 자식이면 부모의 오른쪽 포인터를 null로 합니다.

$\color{white} \colorbox{brown}{B}$ 자식 노드가 1개인 노드를 삭제하는 경우

삭제 대상 노드가 부모 노드의 왼쪽 자식이면 부모의 왼쪽 포인터가 삭제 대상 노드의 자식을 가리키도록 합니다.

삭제 대상 노드가 부모 노드의 오른쪽 자식이면 부모의 오른쪽 포인터가 삭제 대상 노드의 자식을 가리키도록 합니다.

$\color{white} \colorbox{brown}{C}$ 자식 노드가 2개인 노드를 삭제하는 경우

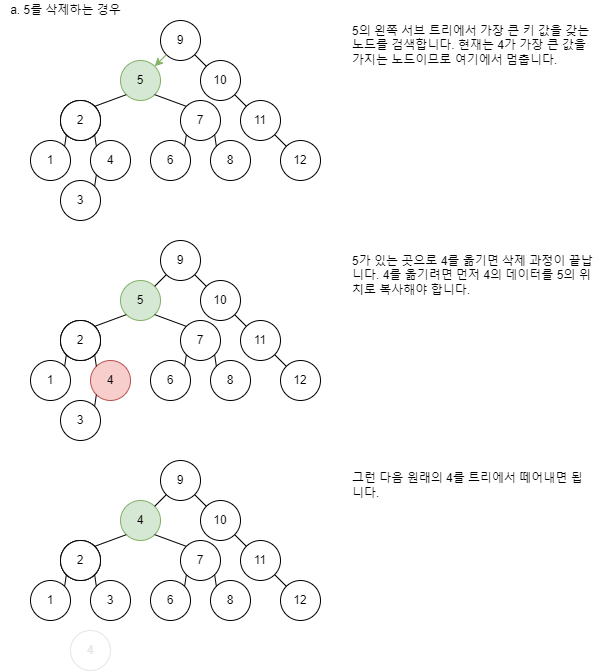
이 과정을 간단히 정리하면 다음과 같습니다.

삭제할 노드의 왼쪽 서브 트리에서 키 값이 가장 큰 노드를 검색합니다.

검색한 노드를 삭제 위치로 옮깁니다(검색한 노드의 데이터를 삭제 대상 노드 위치로 복사합니다).

옮긴 노드를 삭제합니다. 이때

옮긴 노드에 자식이 없으면
'자식 노드가 없는 노드의 삭제 순서'에 따라 노드를 삭제합니다.

옮긴 노드에 자식이 1개만 있으면
'자식 노드가 1개 있는 노드의 삭제 순서'에 따라 노드를 삭제합니다.

remove 메서드는 앞에서 설명한 세 가지 상태에서 노드를 삭제하는 방법을 구현한 메서드입니다.

    // 키 값이 key인 노드를 삭제
    public boolean remove(K key) {
        Node<K, V> p = root;                        // 스캔 중인 노드
        Node<K, V> parent = null;                   // 스캔 중인 노드의 부모 노드
        boolean isLeftChild = true;                 // p는 부모의 왼쪽 자식 노드인가?

        while (true) {
            if (p == null)                          // 더 이상 진행하지 않으면
                return false;                       // 그 키 값은 없습니다.
            int cond = comp(key, p.getKey());       // key와 노드 p의 키 값을 비교
            if (cond == 0)                          // 같으면
                break;                              // 검색 성공
            else {
                parent = p;                         // 가지로 내려가기 전에 부모를 설정
                if (cond < 0) {                     // key 쪽이 작으면
                    isLeftChild = true;             // 왼쪽 자식으로 내려감
                    p = p.left;                     // 왼쪽 서브트리에서 검색
                } else {                            // key 쪽이 크면
                    isLeftChild = false;            // 오른쪽 자식으로 내려감
                    p = p.right;                    // 오른쪽 서브 트리에서 검색
                }
            }
        }

        if (p.left == null) {                   // p에는 왼쪽 자식이 없음
            if (p == root)
                root = p.right;
            else if (isLeftChild)
                parent.left = p.right;          // 부모의 왼쪽 포인터가 오른쪽 자식을 가리킴
            else
                parent.right = p.right;         // 부모의 오른쪽 포인터가 오른쪽 자식을 가리킴
        } else if (p.right == null) {           // p에는 오른족 자식이 없음
            if (p == root)
                root = p.left;
            else if (isLeftChild)
                parent.left = p.left;           // 부모의 왼쪽 포인터가 왼쪽 자식을 가리킴
            else
                parent.right = p.left;          // 부모의 오른쪽 포인터가 왼쪽 자식을 가리킴
        } else {
            parent = p;
            Node<K, V> left = p.left;           // 서브 트리 가운데 가장 큰 노드
            isLeftChild = true;
            while (left.right != null) {        // 가장 큰 노드 left를 검색
                parent = left;
                left = left.right;
                isLeftChild = false;
            }
            p.key = left.key;                   // left의 키 값을 p로 옮김
            p.data = left.data;                 // left의 데이터를 p로 옮김
            if (isLeftChild)
                parent.left = left.left;        // left를 삭제
            else
                parent.right = left.left;       // left를 삭제
        }
        return true;
    }

키 값이 key인 노드를 삭제하는 메서드가 remove입니다.

모든 노드를 출력하는 print 메서드

모든 노드의 키 값을 오름차순으로 출력하는 메서드입니다. 오름차순으로 출력하기 위해 중위 순회 방법으로 트리를 검색합니다.

    // node를 루트로 하는 서브 트리의 노드를 키 값의 오름차순으로 출력
    private void printSubTree(Node node) {
        if (node != null) {
            printSubTree(node.left);        // 왼쪽 서브 트리를 키 값의 오름차순으로 출력
            System.out.println(node.key + " " + node.data);     // node를 출력
            printSubTree(node.right);       // 오른쪽 서브 트리를 키 값의 오름차순으로 출력
        }
    }
    
    // 모든 노드를 키 값의 오름차순으로 출력
    public void print() {
        printSubTree(root);
    }

딱 보면 어떤 식으로 동작하는지 알 수 있습니다.

참고문헌: BohYoh Shibata, 자료구조와 함께 배우는 알고리즘 입문, 이지스퍼블리싱, (2018)

지식 저장소

그리디하게 살자.

트리