[알고리즘] 벨만-포드 알고리즘

박현우·2021년 5월 11일

알고리즘

목록 보기

1/1

벨만 - 포드(Bellman-Ford) 알고리즘이란?

그래프 상의 한 정점으로부터 다른 모든 정점들까지의 최단 경로를 구하는 알고리즘E*V입니다. 다만, 최단 경로를 구하는 또 다른 알고리즘인 다익스트라 알고리즘E*log(V)(우선순위 큐 이용시)보다 훨씬 속도가 느립니다.

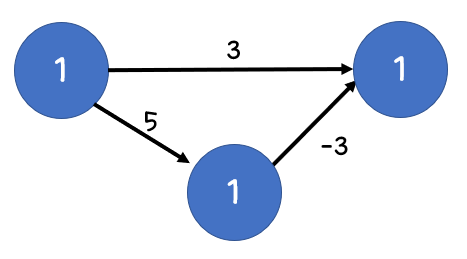
다음과 같이 다익스트라 알고리즘은 노드에서 연결 노드 중 가장 가중치가 낮은 것을 고르기 때문에 원래 답인 2가 아닌 1 -> 3 = 3으로 채택하게 됩니다.
이처럼 가중치가 음수를 가진 그래프에선 사용할 수 없다는 단점이 있습니다.

이를 보완하여 시간을 좀 더 잡아먹더라도 음수의 가중치가 들어있어도, 심지어 음수 사이클이 존재해도 이를 캐치할 수 있는 알고리즘이 벨만-포드 알고리즘입니다.

벨만-포드 알고리즘의 동작과정

벨만-포드 알고리즘은 다익스트라와 다르게 동작합니다.

다익스트라 알고리즘은 가장 가까운 노드를 탐색하여 한 단계를 거칠 때마다 최단 거리를 확정해 나가는 동작과정을 가지고 있고, 벨만 포드 알고리즘은 모든 간선을 확인하는 단계를 V-1만큼 진행하면서 모든 노드간의 최단 거리를 서서히 완화 시켜 동작됩니다.

V-1번 진행했을 때 최단 거리가 확정되는 이유

알고리즘이 실행되면 최단 거리 테이블에 시작 노드가 0, 나머지 노드까지의 거리가 무한인 것을 제외하면 아무 정보도 없습니다.

시작 노드에서 a, b까지의 최단거리를 dist[a], dist[b], b에서 a까지의 가중치를 w(b, a) 라고 정의하면 항상 다음을 만족합니다.
dist[a] <= dist[b] + w(b, a)

a까지의 최단 거리는 b까지의 최단 거리에서 a로 이동하는 경우가 있을수도 있다는 뜻입니다.

출처

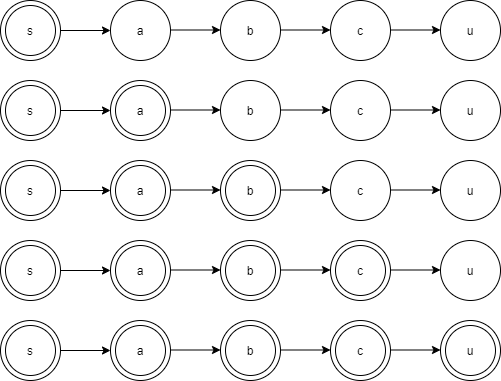
다음 그림과 같이 s에서 u까지의 최단 경로가 다음과 같다고 가정하겠습니다.

처음은 모두 최단 거리를 확정 하지 않았기 때문에 upper[]입니다.
시작 노드인 s는 upper[s] = dist[s] = 0을 보장합니다.
모든 간선을 탐색해 완화 과정을 실행합니다.
그럼 upper[a] <= upper[s] + w(s, a)가 성립하고 upper[s] = dist[s] = 0이기 때문에 upper[a] <= w(s, a)입니다.
그런데 w(s, a)는 s에서 a로 가는 최단 경로여야 합니다. 왜냐하면 최단 경로가 아니면 처음에 가정한 s에서 u까지의 최단 경로에 대한 모순이 생기기 때문입니다.

이것을 반복하면 모든 노드에 대한 최단 거리를 확정 시킬 수 있는데, 위 과정을 정확히 V-1번 반복하면 모든 노드를 확정시킬 수 있습니다.

왜냐하면, 최악의 경우일 때 최대 V개의 정점을 가지고, 그 때의 간선의 개수가 V-1기 때문입니다. 위 그림의 경우과 같습니다.

음수 사이클 찾기

음수 사이클이 없다면 V-1까지 단계를 진행했을 때, 모든 노드는 최단 거리가 확정됩니다.

만약 그 다음 단계를 한번 더 실행했을 때 완화 과정이 이루어 진다면 음수 사이클이 존재한다는 뜻입니다. 그러므로 V까지 단계를 진행하면 마지막 단계에서 사이클이 존재하는지 여부를 판별할 수 있습니다.

벨만-포드 알고리즘의 절차

최단 거리 테이블을 설정합니다.(무한으로 초기화)
시작 노드를 설정합니다.(시작 노드 거리를 0으로 초기화)
V-1번 만큼 다음의 절차를 반복합니다.
3-1. 모든 간선을 확인합니다.
3-2. 간선을 거쳐 다른 노드로 이동하는 비용을 갱신합니다.

코드 (Python)

import sys

input = sys.stdin.readline
n, m = map(int, input().split())
edges = []
inf = 1e9
dist = [inf] * (n + 1)
dist[1] = 0  # 1번 노드에서 출발

for _ in range(m):
    a, b, c = map(int, input().split())
    edges.append((a, b, c))
# 음의 가중치가 존재하기 때문에 다익스트라 사용 불가.
def bellman_ford():
    # 모든 간선을 n-1번 순회하면 음의 순환이 없다는 가정하에
    # 모든 노드까지의 최단 거리를 구할 수 있다.
    # 그러니 총 n번을 순회하고 마지막 n번에 값이 바뀐다면
    # 가중치가 음수인 간선들이 무한 루프를 도는 것이다.
    for i in range(n):
        for a, b, c in edges:
            # 무한이 아니고, 현재 노드를 거쳐 가는 것이 더 비용이 적으면 갱신
            if dist[a] != inf and dist[b] > dist[a] + c:
                if i == n - 1:  # n번째에 갱신된 경우
                    return False
                dist[b] = dist[a] + c
    return True


if not bellman_ford():
    print(-1)
else:
    for x in dist[2:]:
        print(x) if x != inf else print(-1)

박현우