[BOJ 2637] 장난감 조립(Python)

문제

장난감조립

---

문제 해설

이 문제는 문제 특성상 사이클이 생기지 않고 시작 지점과 종료 지점이 명확하기 때문에 위상정렬을 이용해 풀 수 있습니다.
위상 정렬 알고리즘의 단계는 다음과 같습니다.

1. 노드를 연결합니다.
2. 진입 차수를 저장해 놓습니다.
3. 큐 or 스택을 이용해 진입 차수가 0인 노드들을 전부 넣습니다.
4. 노드를 하나씩 빼면서 뺀 노드와 연결되어있는 노드의 연결을 해제합니다. (노드의 차수를 -1 해줍니다.)
5. 차수가 0이라면 큐에 넣어줍니다.
6. 4번을 반복합니다.

이 개념과 문제의 예제를 바탕으로 그림으로 이해해 보겠습니다.

1. 노드를 연결합니다.
문제의 요구 사항을 맞추기 위해 간선이 향하는 곳에 가중치도 함께 저장합니다.

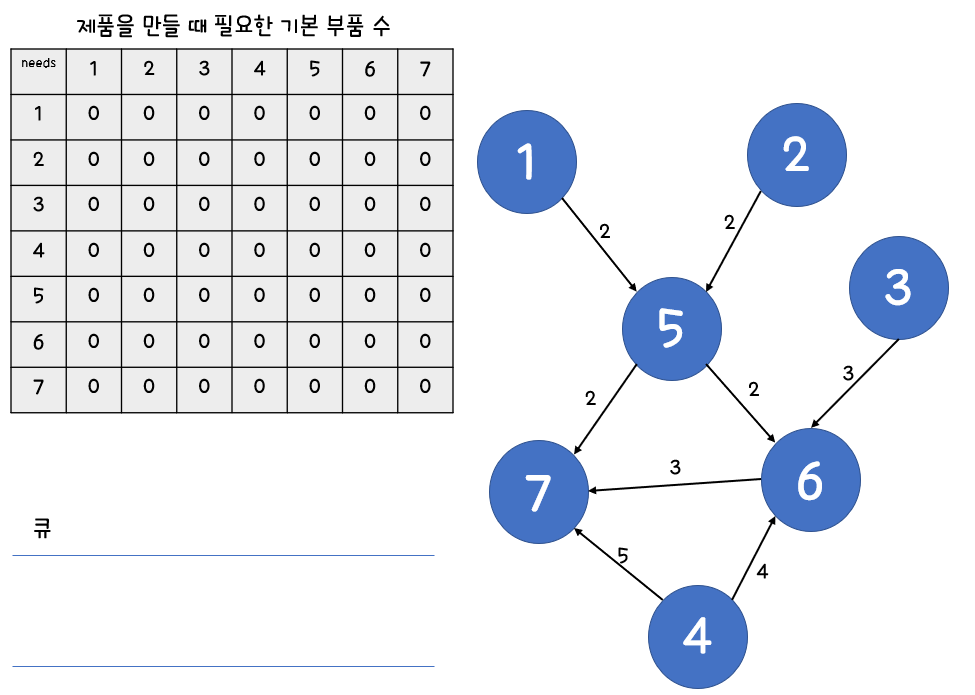
2. 차수가 0인 노드들을 큐에 넣습니다.

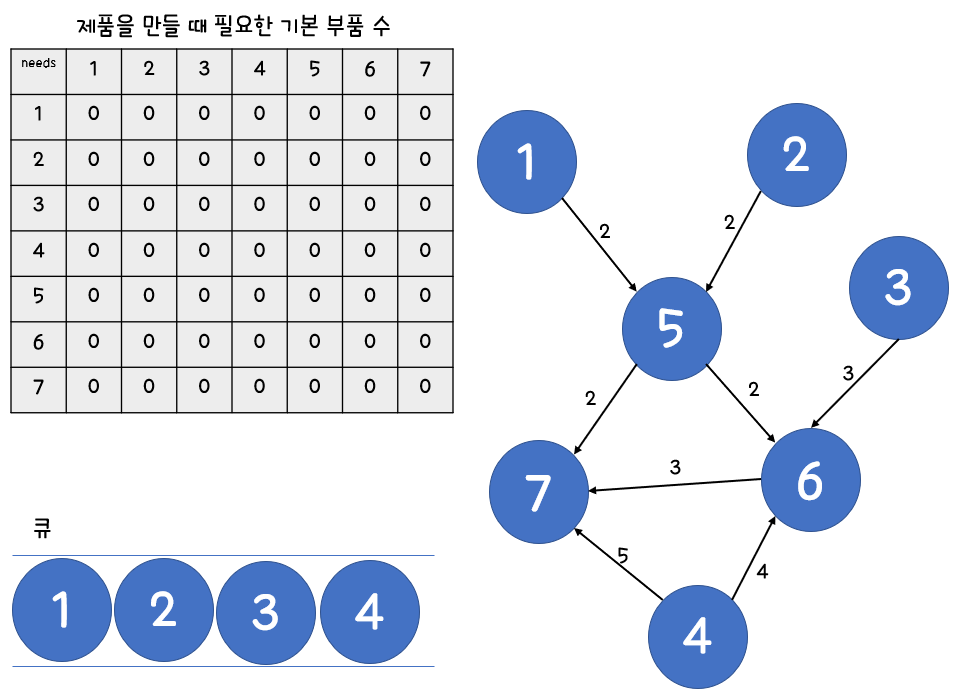
3. 하나씩 빼며 연결 정보를 확인합니다.

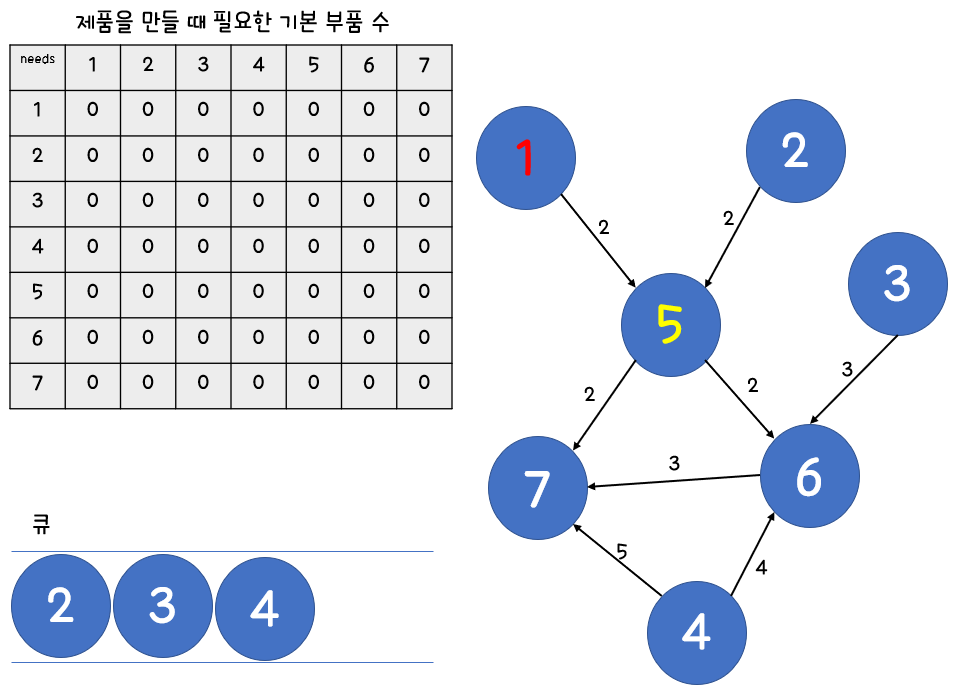
4. 연결된 노드와의 연결을 해제하고 현 노드가 기본 부품이면 가중치, 중간 부품이면 내가 가지고 있는 부품 * 가중치 만큼 더해줍니다.

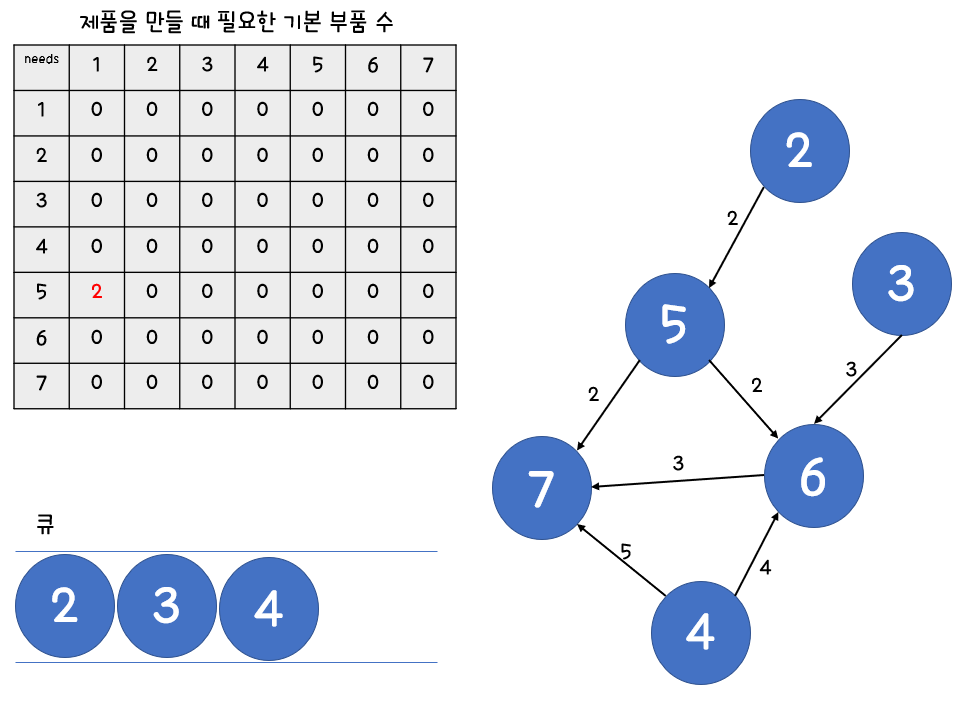
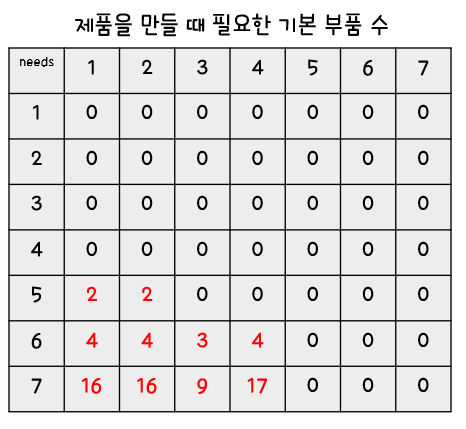
5. 이것을 큐가 빌 때까지 반복하고 needs의 마지막 리스트를 반환합니다.

---

풀이 코드

import sys
from collections import deque

input = sys.stdin.readline
n = int(input())
connect = [[] for _ in range(n + 1)]  # 연결 정보
needs = [[0] * (n + 1) for _ in range(n + 1)]  # 각 제품을 만들때 필요한 부품
q = deque()  # 위상 정렬
degree = [0] * (n + 1)  # 진입 차수
for _ in range(int(input())):
    a, b, c = map(int, input().split())
    connect[b].append((a, c))
    degree[a] += 1

for i in range(1, n + 1):
    # 진입 차수가 0인걸 넣어준다.
    if degree[i] == 0:
        q.append(i)
# 위상 정렬 시작
while q:
    now = q.popleft()
    # 현 제품의 다음 단계 번호, 현 제품이 얼마나 필요한지
    for next, next_need in connect[now]:
        # 만약 현 제품이 기본 부품이면
        if needs[now].count(0) == n + 1:
            needs[next][now] += next_need
        # 현 제품이 중간 부품이면
        else:
            for i in range(1, n + 1):
                needs[next][i] += needs[now][i] * next_need
        # 차수 -1
        degree[next] -= 1
        if degree[next] == 0:
            # 차수 0이면 큐에 넣음
            q.append(next)
for x in enumerate(needs[n]):
    if x[1] > 0:
        print(*x)
print(needs)

---