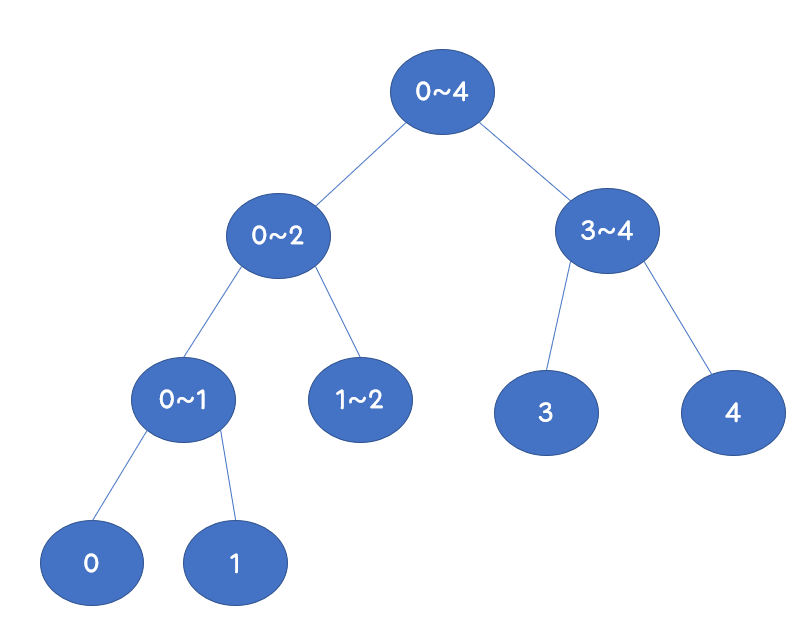
세그먼트 트리란?
특정 구간의 구간 합을 이진 트리의 구조로 저장하여 접근하는 자료 구조의 하나입니다.
일반적으로 구간 합을 구하는 방식은 다음과 같습니다.
ex) arr[45] ~ arr[67]의 합을 구하세요
- arr[45] + arr[46] + ... + arr[67] =
O(N) = N- S[67] - S[45] =
O(N) = N, S[i] == arr[0]~arr[i]까지의 합
언뜻 보기에는 다를게 없어 보이지만, 특정 구간의 합을 N번 구해야 한다면 둘의 시간 차이는 N^2과 N으로 심하게 차이가 납니다.
여기에서 만약 i번 인덱스의 값을 바꾸는 연산도 추가한다면, 두번째 방식도 값이 변경될 때마다 S[0] ~ S[i]번까지 모두 고쳐야 하기 때문에 최악의 경우 N^2의 시간 복잡도를 가집니다.
이런 값을 바꾸는 연산이 추가된다면 각 노드마다 구간 합을 가지고 있는 세그먼트 트리의 구조를 활용하여 시간복잡도를 줄일 수 있습니다.
이진 트리의 구조라 탐색에 log(N), 값을 변경하는데에 log(N)의 시간 복잡도를 가집니다.
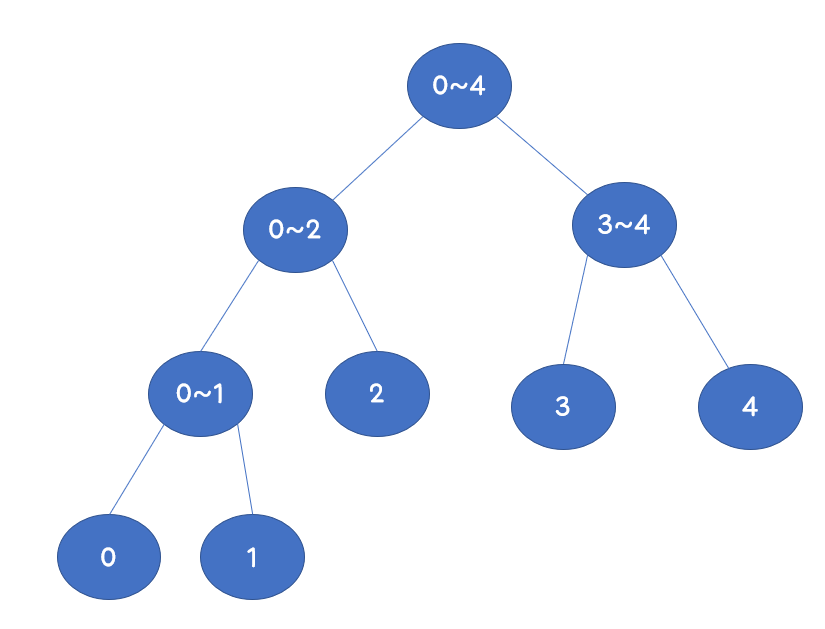
그림과 같이 각 리프노드는 배열의 값, 다른 노드는 자식노드의 합을 담고 있습니다.
저 그림에서 0~3번 까지의 합을 구한다면 다음과 같습니다.
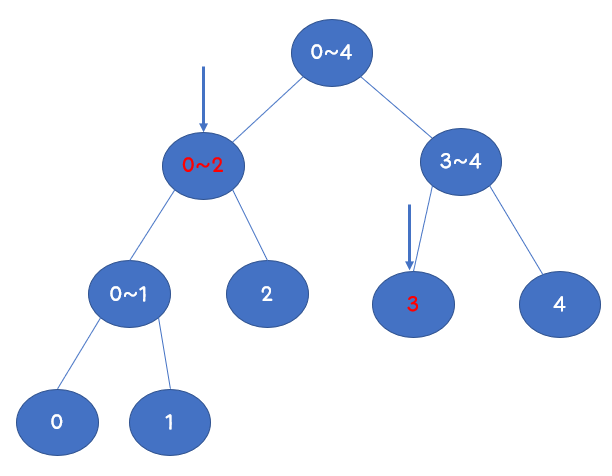
저 그림에서 3번 인덱스의 값을 6으로 변경한다면 다음과 같습니다.
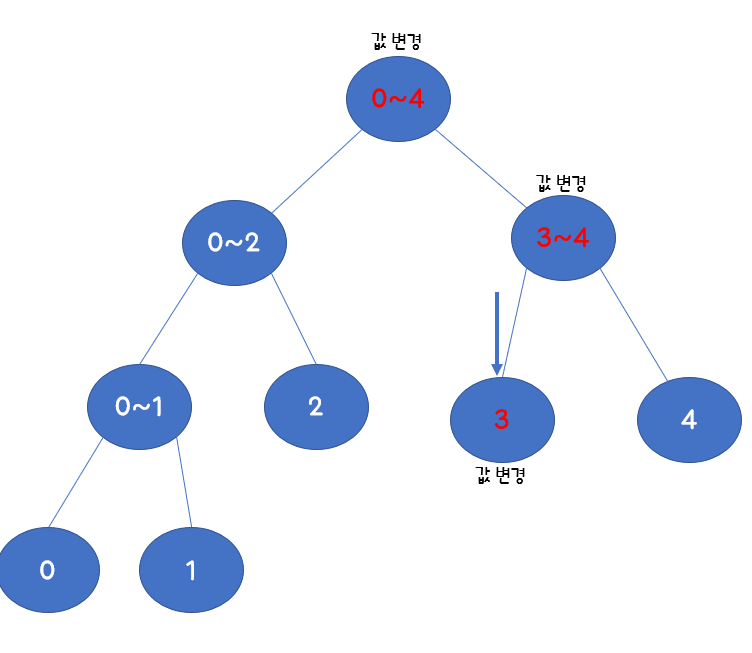
세그먼트 트리의 프로그램 구조
세그먼트 트리는 다음과 같은 메소드로 구성 되어있습니다.
- 세그먼트 트리의 구조를 형성하고 값을 저장하는 메소드(초기화)
- 세그먼트 트리의 노드의 값을 꺼내는 메소드(구간 합 구하기)
- 특정 인덱스의 값을 변경하는 메소드
노드 값 저장하기
각 노드마다 구간 합을 저장해야 하기 때문에 이진 트리 구조의 세그먼트 트리는 2^(1+log(N)) - 1만큼의 배열 크기를 설정해 주어야 합니다. 계산이 까다롭기 때문에 항상 넉넉히 배열의 크기를 설정해 주는 것이 필요합니다.
세그먼트 트리 초기화
# 세그먼트 트리 초기화
def init(node, start, end):
if start == end:
tree[node] = arr[start]
return tree[node]
mid = (start + end) // 2
# 리프 노드가 아닐 때 자식 노드의 리턴 값 저장
tree[node] += init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end)
return tree[node]각 노드의 값을 담는 tree에 누적 합을 저장합니다.
구간 합 구하기
def prepix_sum(start, end, left, right, node):
# 필요 없는 구간이므로 버림.
if start > right or end < left:
return 0
# 필요한 구간은 해당 tree 값 리턴
# 굳이 리프까지 갈 필요 X
if left <= start and end <= right:
return tree[node]
mid = (start + end) // 2
# init과 마찬가지로 자식 노드의 리턴 값을 더해 리턴
return prepix_sum(start, mid, left, right, node * 2) + prepix_sum(
mid + 1, end, left, right, node * 2 + 1
)구해야 하는 구간 left right와 실제 탐색할 구간start, end를 매개변수로 두고 탐색하는 메소드 입니다. start와 end를 요구사항에 맞춰 줄여 나가며 필요 없는 구간은 바로 버리고 필요한 구간은 바로 return 합니다.
값 변경하기
# 값 변경하기, 반드시 한 줄로 탐색을 한다.
def update(node, start, end, index, diff) :
if index < start or index > end :
return
tree[node] += diff
if start != end :
update(node*2, start, (start+end)//2, index, diff)
update(node*2+1, (start+end)//2+1, end, index, diff)매개변수로 해당 인덱스의 값과 변경하려는 상수의 차이인 diff를 줬습니다. 루트부터 해당 인덱스가 저장되어있는 리프까지 전부 변경해주는 코드입니다.
혹은 리프까지 탐색 후 return 값으로 diff를 주어 값을 변경하는 방식의 코드로 구현하셔도 무방합니다.
전체코드 (BOJ 2042)
import sys
input = sys.stdin.readline
# 세그먼트 트리 초기화
def init(node, start, end):
if start == end:
tree[node] = arr[start]
return tree[node]
mid = (start + end) // 2
# 리프 노드가 아닐 때 자식 노드의 리턴 값 저장
tree[node] += init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end)
return tree[node]
# 구간 합
def prepix_sum(start, end, left, right, node):
# 필요 없는 구간이므로 버림.
if start > right or end < left:
return 0
# 필요한 구간은 해당 tree 값 리턴
# 굳이 리프까지 갈 필요 X
if left <= start and end <= right:
return tree[node]
mid = (start + end) // 2
# init과 마찬가지로 자식 노드의 리턴 값을 더해 리턴
return prepix_sum(start, mid, left, right, node * 2) + prepix_sum(
mid + 1, end, left, right, node * 2 + 1
)
# 값 변경하기, 반드시 한 줄로 탐색을 한다.
# 해당 인덱스를 리프 노드에서 찾은 뒤, 리턴되며 값을 전부 변경
# 리턴 값은 원래의 값과의 차이
def update(index, start, end, node, value):
# 리프 노드를 찾았고, 값의 차이를 리턴
if index == start == end:
dif = value - tree[node]
tree[node] = value
return dif
mid = (start + end) // 2
dif = 0
if index <= mid:
dif = update(index, start, mid, node * 2, value)
tree[node] += dif
else:
dif = update(index, mid + 1, end, node * 2 + 1, value)
tree[node] += dif
return dif
arr = []
tree = [0] * 3000000 # 구간 합 저장.
n, m, k = map(int, input().split())
# 초기 값 순서대로 저장
for _ in range(n):
arr.append(int(input()))
init(1, 0, n - 1)
for _ in range(m + k):
a, b, c = map(int, input().split())
if a == 1: # 변경
update(b - 1, 0, n - 1, 1, c)
else: # 출력
print(prepix_sum(0, n - 1, b - 1, c - 1, 1))