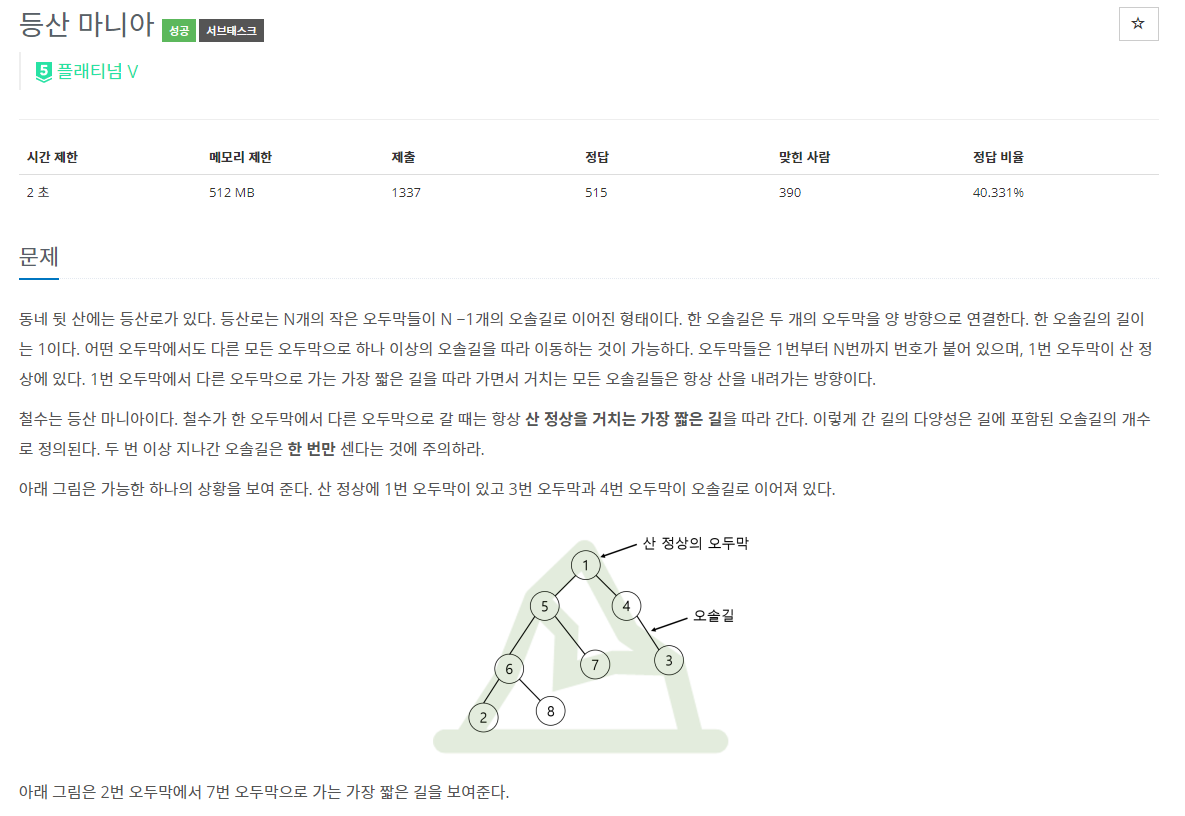

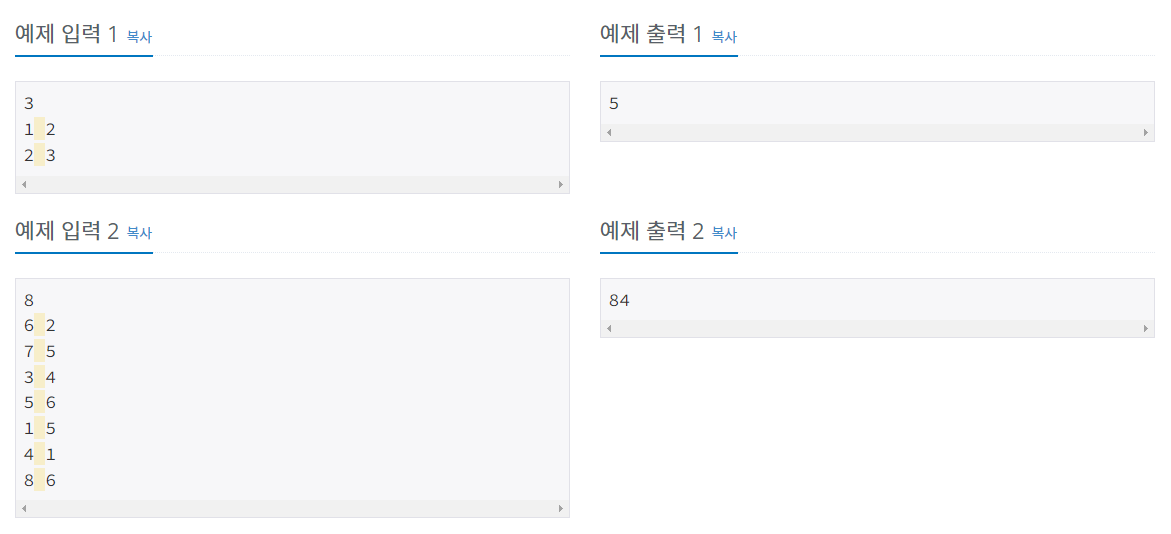
문제 설명
- https://www.acmicpc.net/problem/20188
- A에서 B로 이동할 때 항상 루트(1)를 거쳐서 이동합니다.
루트를 거치는 방식으로 A에서 B로 이동할 때 이동하면서 지나간 길의 개수를 다양성이라고 합니다. A에서 B로 이동하는 중에 같은 길은 여러번 지나가도 한 번만 셉니다.
1<=i<j<=N을 만족하는 모든 (i,j)에 대해 i에서 j로 이동하는 다양성의 합을 구하는 문제입니다.
접근법
- 혼자서 풀지 못해 풀이 영상을 참고했습니다.
- 처음 생각한 방법은 LCA를 활용하는 풀이였습니다.
A에서 B까지 이동할 때 다양성 = A에서 LCA까지의 다양성 + B에서 LCA까지의 다양성 + LCA에서 루트(1)까지의 다양성이라고 생각했습니다. 아이디어는 맞지만 N = 300,000으로 시간초과가 발생할 거 같았습니다.
- 이 문제의 핵심은 노드보다
간선을 중심으로 생각하는 겁니다. 전체에서 특정 길이 몇번 이용되는가를 생각하면 좋습니다.
- 간선을 중심으로 생각했을 때 가장 강력한 규칙은
해당 간선 아래에 있는 노드는 반드시 해당 간선을 지난다입니다. 이렇게 생각했을 때 또 하나 중요한 점은 두 점이 해당 간선 아래 있어도 지나고, 한 점만 해당 간선 아래 있어도 해당 간선을 지난다는 겁니다.
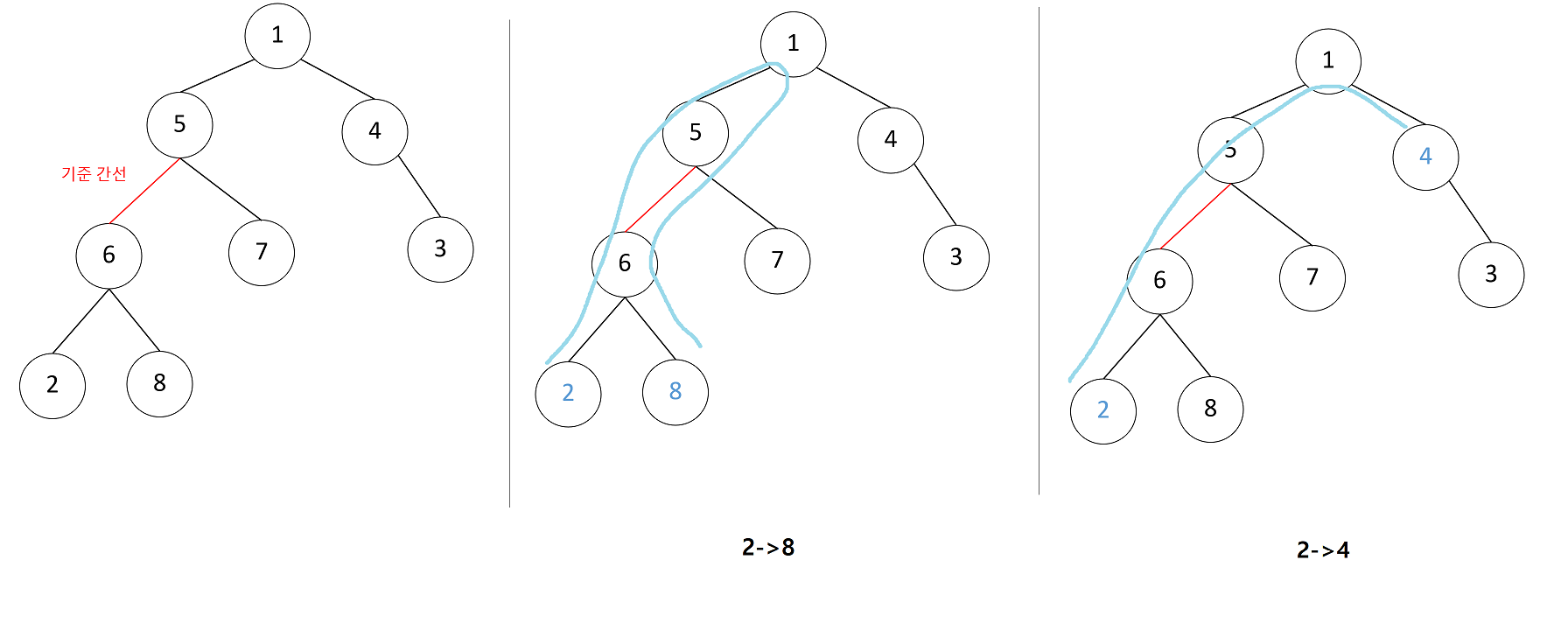
- 5와 6 사이의 간선을 기준으로 했을 때
2는 해당 간선 아래 있습니다. 그렇기 때문에 2에서 어디를 향해 가더라도 기준 간선을 지나게 됩니다.
- 반대로 해당 간선을 지나지 않으려면
두 노드 모두 해당 간선 아래에 있지 않아야 합니다. 위 그림에서 5->7, 4->3, 1->5,... 처럼 두 점 모두 기준 간선 아래에 있지 않으면 해당 간선을 지나지 않습니다.
- 결국 총 8C2개의 경우의 수 중
해당 간선 아래에 있는 3개(2,6,8)를 제외한 임의의 두 점(1,3,4,5,7)을 이은 경로에서는 기준 간선이 활용되지 않습니다. 모든 간선에 대해 해당 계산을 적용하면 최종 정답을 얻을 수 있습니다.
정답
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
Map<Integer,List<Integer>> graph = new HashMap<Integer,List<Integer>>();
for (int i = 0; i < N-1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
makeGraph(graph,a,b);
makeGraph(graph,b,a);
}
int[] subTree = new int[N+1];
DFS(1,subTree,new boolean[N+1],graph);
long answer = 0;
for (int i = 2; i <= N; i++) {
int X = N - subTree[i];
answer += selectTwoFromNum(N) - selectTwoFromNum(X);
}
System.out.println(answer);
}
public static long selectTwoFromNum(int num) {
return 1L*num*(num-1)/2;
}
public static int DFS(int now, int[] subTree, boolean[] v, Map<Integer,List<Integer>> graph) {
v[now] = true;
subTree[now] = 1;
if(graph.containsKey(now)) {
for (int next : graph.get(now)) {
if(v[next]) continue;
subTree[now] += DFS(next,subTree,v,graph);
}
}
return subTree[now];
}
public static void makeGraph(Map<Integer,List<Integer>> graph, int from, int to) {
if(graph.containsKey(from)) {
graph.get(from).add(to);
}else {
List<Integer> temp = new ArrayList<Integer>();
temp.add(to);
graph.put(from, temp);
}
}
}
기타
- HashMap의 containsKey의 시간복잡도는 O(1)입니다.





