들어가기 앞서
- 이번 포스팅은 인터넷에서 정보를 찾아본 뒤 이해가 쉽게 되지 않아
나름의 생각을 설명으로 풀어쓴 글입니다. 실제 이론과 내용은 이와 다를 수 있음을 감안하고 읽어주시면 감사하겠습니다.
보수란
보충해주는 수- (
10진법에서)3에 대한10의 보수는73을10으로 만들기 위해서는7이 필요하다는 의미입니다.
(2진법에서) 1의 보수
-
인터넷에서
1의 보수에 대한 설명을 쉽게0과 1을 바꾼 값으로 설명하고 있습니다.- ex)
1001의 1의 보수 ->0110
- ex)
-
2진수
1001이 있을 때 위에서 설명한 정의를 적용하면 다음과 같습니다.- (
2진법에서)1001에 대한1의 보수는0110다1001을1로 만들기 위해서는0110가 필요하다.1001+0110은1이 아니기 때문에1001을1로 만든다는 문장은 매우 어색합니다.
- 그래서
1로 만든다는 걸모든 자리수의 값을 1로 만든다로 바꿔보았습니다. 1001을1111로 만들기 위해서는0110이 필요하다.
- (
결론
- 1의 보수는
A가111...11이 되기 위해 필요한 수B이다. - 2진수에서
111...11-A는A에서 0과 1의 자리를 바꾼 값과 같다.
(2진법에서) 2의 보수
- 인터넷에서
2의 보수는1의 보수 +1로 설명하고 있습니다.- ex)
1001의 2의 보수 ->0111(0110+1)
- ex)
- 2의 보수 역시 처음의 정의를 적용하면 어색한 문장이 됩니다.
- (
2진법에서)1001을2로 만들기 위해서는0111이 필요하다. - 그래서
2로 만든다는 걸다음 자릿수로 만든다로 표현해 바꿔보겠습니다.1001을10000으로 만들기 위해0111이 필요하다.2진법에서2라는 숫자는 존재하지 않고,2를 표현하려면 자릿수를 변경시켜야 하기 때문에 자릿수를 변경시킨다는 의미가 어색하지 않습니다.
- (
결론
- 2의 보수는
A가100...0(A보다 한자리 더 많은 수)이 되 위해 필요한 수B이다. - 2진수에서
100...00은A+A의 1의 보수+1이다.- 왜냐하면
A+A의 1의 보수=111...11이기 때문 A의 1의 보수+1을 묶어A의 2의 보수로 볼 수 있다.
- 왜냐하면
뺄셈
보수는뺄셈(음수)을 위해 도입된 개념이다.- 컴퓨터는
A-B를A+(-B)로 바꾸어 계산해야 합니다.
- 컴퓨터는
- 컴퓨터는
부호비트를 통해음수를 표현하기도 합니다. 비트의 가장 왼쪽 값은 부호를 나타내는 칸으로 활용하기로 약속하는 것이죠.- 가장 왼쪽 비트값이
0이면양수다 - 가장 왼쪽 비트값이
1이면음수다- 하지만
부호비트가 무조건적인건 아닙니다.1000이 있을 때 이를8로 볼 것인지-1로 볼 것인지는 경우에 따라 다릅니다.
- 하지만
- 가장 왼쪽 비트값이
- 보수를 이용한 뺄셈은
1의 보수,2의 보수둘 다 가능합니다.1의 보수를 활용한 계산에는1의 보수를 구한 뒤+1을 더하는 과정이 필요합니다. 이는 결국2의 보수를 계산하는 것과 동일한 행위이므로 사실상1의 보수를 활용한 뺄셈과2의 보수를 활용한 뺄셈은 같습니다.
- 2의 보수를 활용한 뺄셈방법은 다음과 같습니다.(
A-B)빼는 수(B)의2의 보수를 구합니다.(B')A와빼는 수의 2의 보수(B')를 더합니다.- 더했을 때 최상위비트의 자리올림이 생겼다면 자리올림된 부분을 제외한 값이
A-B의 결과입니다. - 더했을 때 자리올림이 생기지 않았다면 해당 계산값(
A+B')의2의 보수를 구한 값에-부호를 붙여준 값이A-B의 결과값입니다.(B>A인 경우입니다)
- 더했을 때 최상위비트의 자리올림이 생겼다면 자리올림된 부분을 제외한 값이
계산
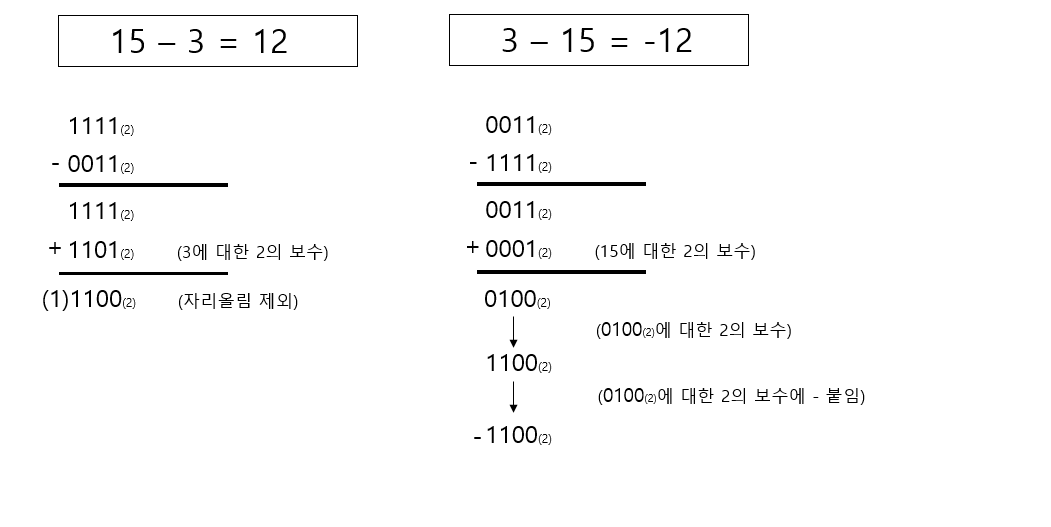
마치며
- 보수의 뺄셈 계산이 왜 저렇게 되어야 하는지에 대한 명확한 설명을 못해서 아쉽다

