백준 1005번: ACM Craft

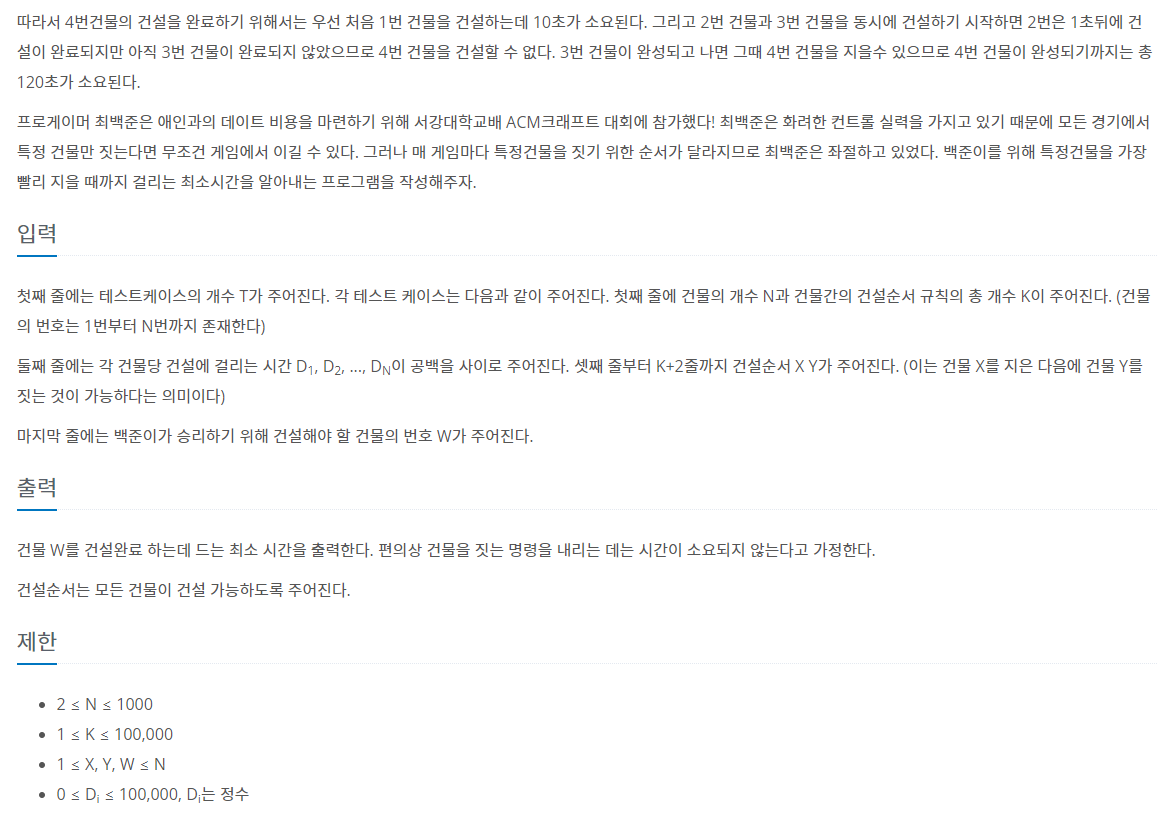
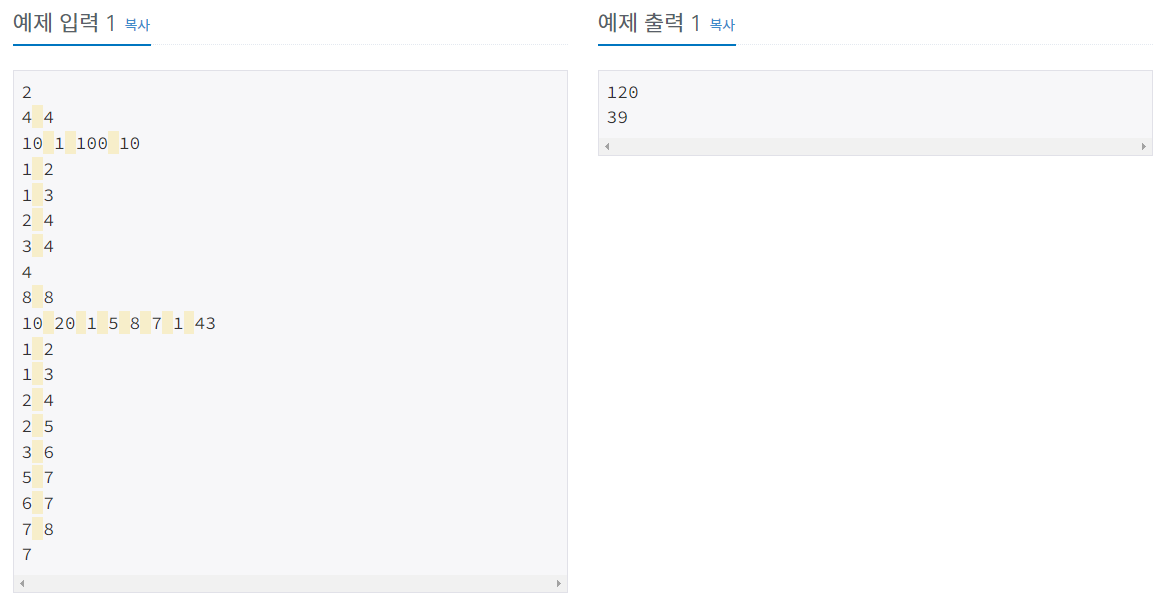
문제 설명

• https://www.acmicpc.net/problem/1005

접근법

• 위상 정렬을 이용하는 문제입니다.
  선후관계가 존재하는 그래프 문제는 위상 정렬을 활용하기 좋습니다.

• 7번 건물을 짓기 위해 5번과 6번이 필요할 때 원래라면 5번과 6번이 모두 완료된 시점에 7번건물의 시간을 계산해야 합니다. 그리고 이 때 7번 건물을 짓기 위해 걸리는 시간은 5번 건물과 6번 건물 중 완료까지 더 오래 걸리는 건물의 최종 시간 + 7번 건물을 짓기 위해 걸리는 시간 입니다.
  저는 두 건물이 모두 완성됐다는 걸 확인하지 않고 각 건물이 완성됐을 때 7번 건물에 대한 시간을 계산했습니다. 그리고 이후 들어온 값이 더 크다면 더 큰 값으로 갱신해 줬습니다.

정답

import java.util.*;
import java.io.*;

public class Main {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int T = Integer.parseInt(br.readLine());
		StringBuilder sb = new StringBuilder();
		for (int t = 0; t < T; t++) {
			
			StringTokenizer st = new StringTokenizer(br.readLine());
			int N = Integer.parseInt(st.nextToken());
			int K = Integer.parseInt(st.nextToken());
			int[] delayTimeToBuild = new int[N+1];
			st = new StringTokenizer(br.readLine());
			for (int i = 1; i <= N; i++) {
				delayTimeToBuild[i] = Integer.parseInt(st.nextToken());
			}
			
			// 진입차수
			int[] inDegree = new int[N+1];
			
			// 관계를 나타내는 그래프 
			Map<Integer,List<Integer>> graph = new HashMap<Integer,List<Integer>>();
			for (int i = 0; i < K; i++) {
				st = new StringTokenizer(br.readLine());
				int a = Integer.parseInt(st.nextToken());
				int b = Integer.parseInt(st.nextToken());
				
				// 진입차수 설정
				inDegree[b]++;
				
				if(graph.containsKey(a)) {
					graph.get(a).add(b);
				}else {
					List<Integer> temp = new ArrayList<Integer>();
					temp.add(b);
					graph.put(a,temp);
				}
			}
			
			// 우선순위 큐
			PriorityQueue<Integer> pq = new PriorityQueue<Integer>();
			// dp[i] = i번째 건물을 짓기 위해 걸리는 시간
			int[] dp = new int[N+1];
			
			// 초기값 설정
			for (int i = 1; i <= N; i++) {
				if(inDegree[i] == 0) {
					pq.add(i); // 진입차수가 0인 값을 pq에 넣음
					dp[i] = delayTimeToBuild[i]; // 진입차수가 0인 건물을 짓기 위해 걸리는 시간
				} 
			}
			
			while(!pq.isEmpty()) {
				int now = pq.poll(); // 진입차수가 0인 건물
				if(!graph.containsKey(now)) continue;
				for (int next : graph.get(now)) {
					inDegree[next]--; // now의 진입차수가 0이 되었기 때문에 next의 진입차수는 1 내려간다
					if(inDegree[next] == 0) { // next의 진입차수가 0이되면 다음 값을 찾기 위해 pq에 추가
						pq.add(next);
					}
					/*
					 * 현재 그래프는 value(list)의 값들은 key 값을 선수조건으로 가짐을 나타냅니다.
					 * {a:[b,c,d]}일 때 b를 짓기 위해 a가 먼저 건설되어야 하는 건 맞지만, a를 건설하면 반드시 b를 건설할 수 있다는 의미는 아닙니다.
					 * 5->7, 6->7일 때 7번 건물을 지을려면 '5번과 6번이 모두' 미리 지어져 있어야 합니다.
					 * 그렇기 때문에 우리는 5번을 지었을 때 7번 시간을 한번 계산하고,
					 * 6번을 지었을 때 7번 시간을 또 계산한 뒤 둘 중 시간이 큰 값을 선택합니다.
					 */
					dp[next] = Math.max(dp[now]+delayTimeToBuild[next], dp[next]);
				}
			}
			
			// 정답 출력
			int W = Integer.parseInt(br.readLine());
			sb.append(dp[W]);
			sb.append("\n");			
		}
		System.out.println(sb.toString());
	}
	
}