백준 10610번: 30

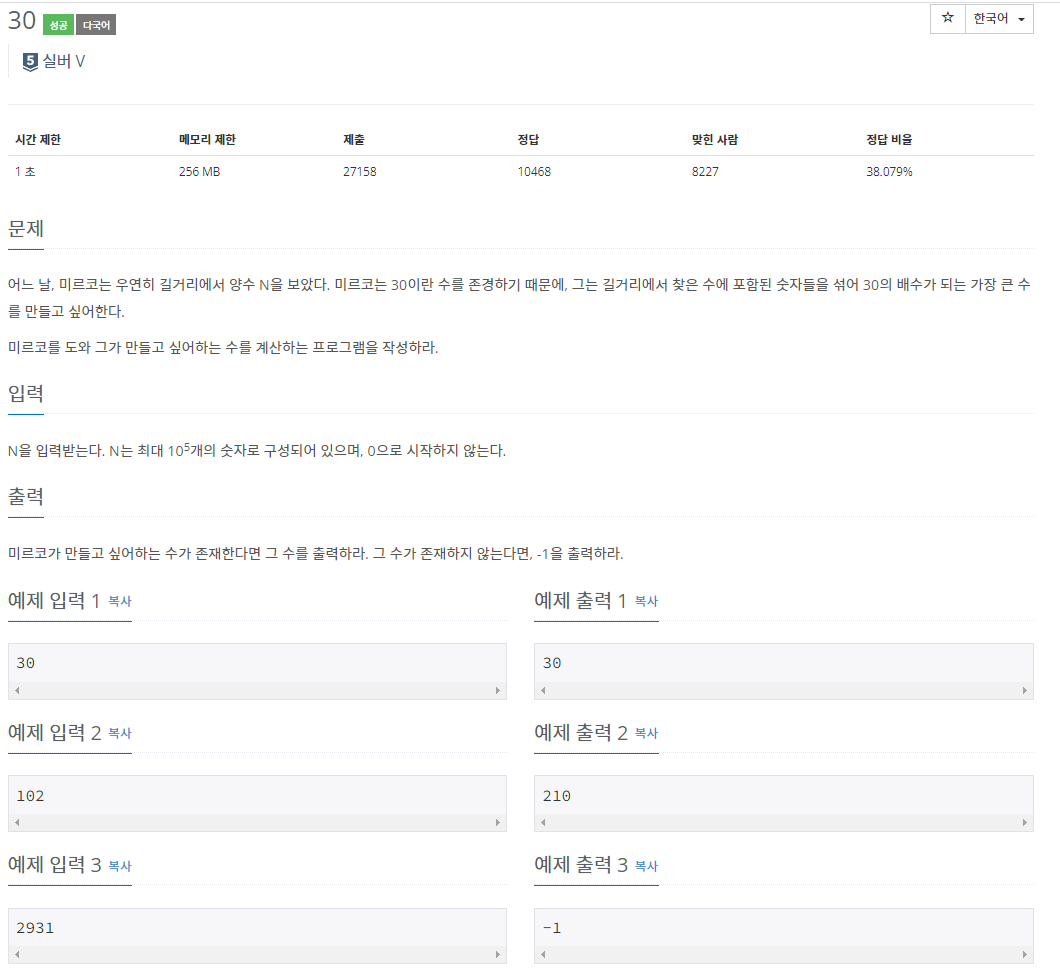
문제 설명

• 주어진 숫자를 가장 큰 30의 배수로 재배열 하는 문제입니다.

접근법

• 30의 배수는 마지막 수를 제외한 수가 3의 배수인 수입니다.
  • 30의 배수 = [3의배수인 수]x10
• 각 자릿수의 합이 3의 배수이면 전체 수는 3의 배수입니다.
  • 4자리 수 abcd가 있다고 가정해 보겠습니다.
  • 이는 1000a + 100b+ 10c +d으로 표현할 수 있습니다.
  • = (999a+a)+(99b+b)+(9c+c)+d
    • 모든 10^n은 999...9+1로 표현이 가능합니다.
  • = (999a+99b+9c)+(a+b+c+d)
  • = 3(333a+33b+3c)+(a+b+c+d)
    • 각 자릿수의 합이 3의 배수이면 (a+b+c+d) = 3k이므로
  • 4자리 수 abcd = 3(333a+33b+c+k) = 3의배수 입니다.
• 각 자릿수의 합으로 3의 배수가 결정되기 때문에 자릿수를 어떻게 배치하든 3의 배수입니다.
  • a+b+c+d가 3의 배수이면 abcd,cabd,dabc,... 등 모든 조합이 다 3의 배수입니다.
  • 그렇기 때문에 3의 배수여부를 확인했다면 내림차순정렬을 통해 가장 큰 3의 배수를 만들 수 있습니다.

정답

n = input() # 문자열로 받습니다
sum_ = 0
for i in n:
    sum_+=int(i)
    
if sum_%3 == 0 and '0' in n:    
    char_answer = ''.join(sorted(n)[::-1])
    print(int(char_answer))
else:
    print(-1)

기타

• sum_%3 == 0대신 eval('+'.join(n))%3로 3의 배수 여부를 판단했더니 recursionerror가 발생했습니다. 로컬에서 테스트케이스 테스트를 했을 때에는 정상적으로 작동되었는데 recursionerror가 발생하는 케이스가 존재하는건지, 로컬과 제출환경에 무언가 차이점이 있는지 잘 모르겠지만 에러때문에 for문을 사용하는 코드로 변경했습니다.
• 3의 배수 판별법과 동일한 원리로 9의 배수도 구할 수 있습니다.
  • 모든 자릿수의 합이 9의 배수이면 전체 수는 9의 배수입니다.