백준 10986번: 나머지 합

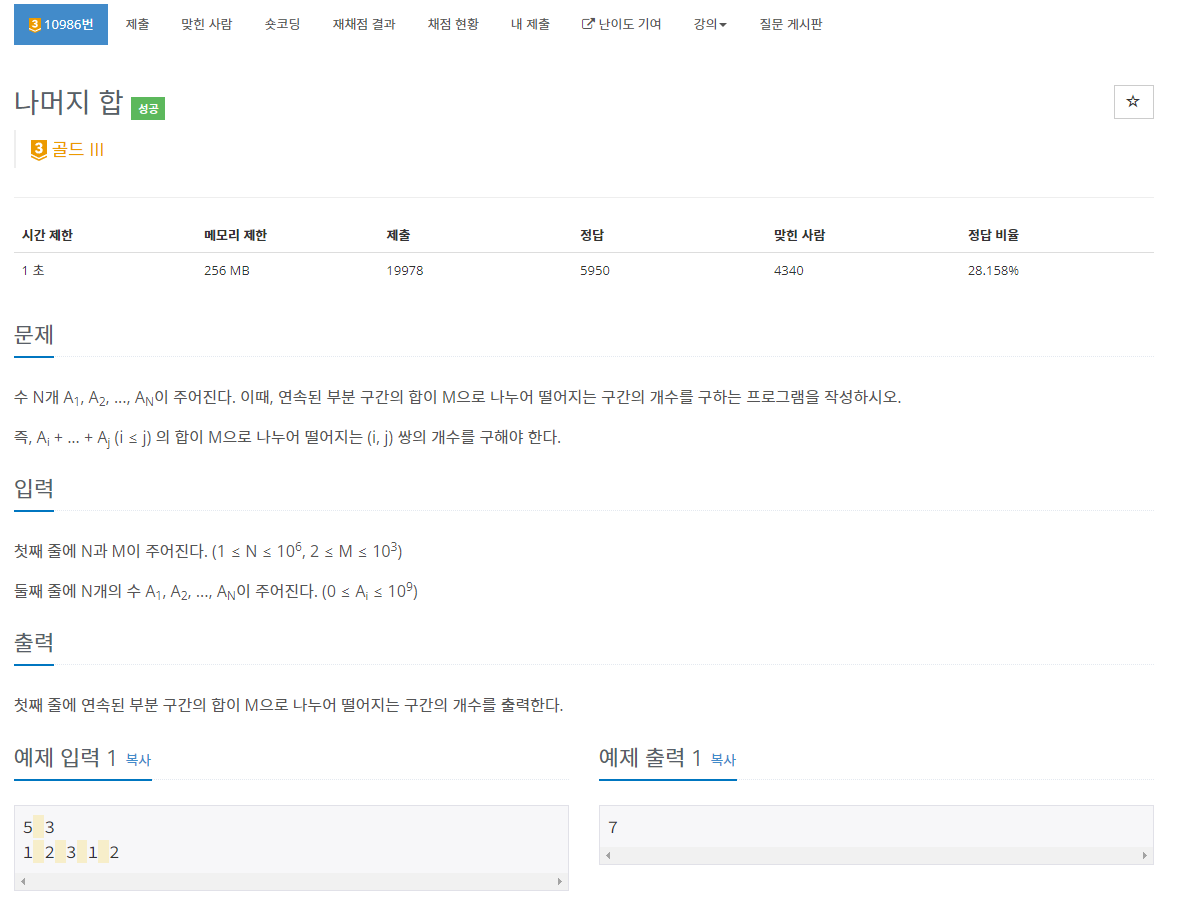
문제 설명

• 연속된 구간의 합이 M으로 나눠떨어지는 구간의 개수를 구하는 문제입니다.

접근법

• 연속된 구간의 합이기 때문에 누적합, 투 포인터등의 방법이 떠올랐습니다. 투 포인터의 경우 어떤 조건에서 포인터를 이동시켜야 하는지가 명확하지 않아 부적절하다 생각했습니다.
• 누적합을 구하면 모든 경우를 살펴보는 O(N^2)의 풀이법을 쉽게 떠올릴 수 있습니다. 하지만 입력값 N이 10^6으로 O(N^2)풀이법은 시간초과가 발생합니다.
• i~j까지의 누적합은 cumSum[j] - cumSum[i-1]입니다. 이 문제는 (cumSum[j] - cumSum[i-1])%M == 0을 만족해야 하고, 이 식은 cumSum[j]%M == cumSum[i-1]%M과 동일합니다. cumSum[x]%M는 O(N^2)이 아닌 O(N)으로 미리 계산해둘 수 있습니다.
  • 즉 누적합%M의 값이 같은 두 i와 j를 선택하면 조건을 만족합니다.
  • 이 외에 처음부터 cumSum[x]의 값이 0이면 조건을 만족합니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		st = new StringTokenizer(br.readLine());
		long[] cumSum = new long[N+1];
		int[] modCnt = new int[M];
		long answer = 0;
		for (int i = 1; i <= N; i++) {
			cumSum[i] = (Integer.parseInt(st.nextToken()) + cumSum[i-1]); // 계산과정에서 int를 초과할 수 있습니다.
			int modResult = (int)(cumSum[i]%M);
			modCnt[modResult]++;
		}
		answer += modCnt[0];
		for (int i = 0; i < M; i++) {
			int num = modCnt[i];
			if(num == 0) continue;
			answer += ((long)num*(num-1))/2; // 계산과정에서 int를 초과할 수 있습니다.
		}



		// 시간초과
//		for (int i = 1; i <= N; i++) {
//			for (int j = 0; j < i; j++) {
//				if((cumSum[i] - cumSum[j])%M == 0) answer++;
//			}
//		}
		System.out.println(answer);
	}
}