백준 11048번: 이동하기

문제 설명

• (1,1)에서 (N,M)로 가야 합니다.
• 오른쪽으로 한 칸, 아래로 한 칸, 오른쪽 아래 대각선으로 한 칸 중 하나의 방법으로 움직일 수 있습니다.
• 칸으로 이동하면 해당 칸에 적힌 숫자만큼 사탕을 얻습니다. 최대 몇 개의 사탕을 얻을 수 있는지를 구해야 합니다.

접근법

• 이 문제는 현재 칸에서 어디로 갈 수 있는가? 보다 현재 칸으로 어떻게 올 수 있는가?를 기준으로 생각하는 게 더 쉽습니다.

1. 현재까지 모은 사탕의 개수는 이전 칸의 사탕 개수를 더해 표현할 수 있습니다.
   
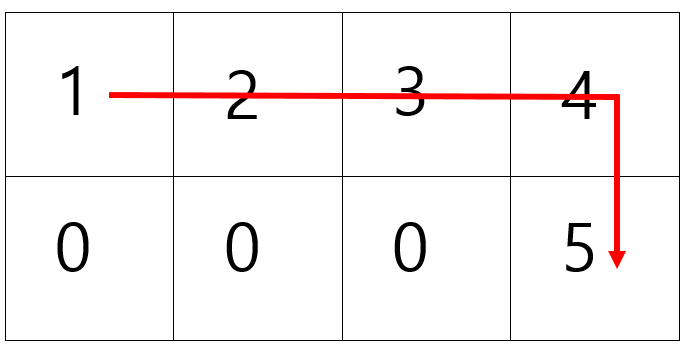
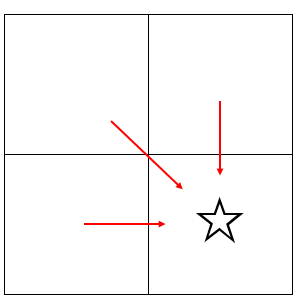
   위와 같이 사탕이 뿌려진 길을 빨간색 방향으로 왔다면 각 칸에서 가진 사탕의 총 량은 다음과 같습니다
   

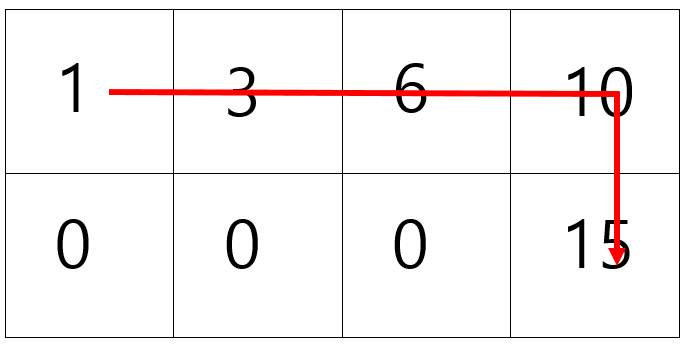
즉 현재 칸까지 오면서 모은 사탕의 개수 = 이전 칸까지 오면서 모은 사탕의 개수 + 현재 칸의 사탕이 성립합니다.

2. 우리가 움직이는 방법이 3 가지 이기 때문에 특정 칸(☆)에 도달하는 방법도 3가지 입니다.

• 왼쪽에서 접근한다.

• 위에서 접근한다.

• 왼쪽 위에서 대각선으로 접근한다.

  

• 그렇다면 ☆에 최대한 많은 사탕을 가지고 접근하는 방법은 어떻게 될까요?

  • 그건 ☆로 접근할 수 있는 3칸 중 사탕을 가장 많이 모은 곳에서 ☆로 오는 것입니다.

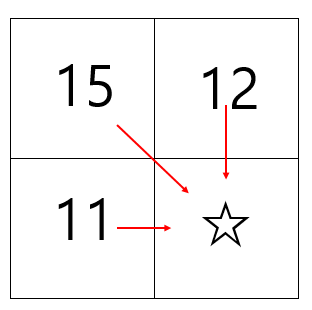
다음과 같다면 우리는 15에서 ☆로 가는 게 가장 현명한 방법일 것입니다.

• 우리는 1과 2의 방법을 모든 칸에 적용시키면 정답을 구할 수 있습니다.
  
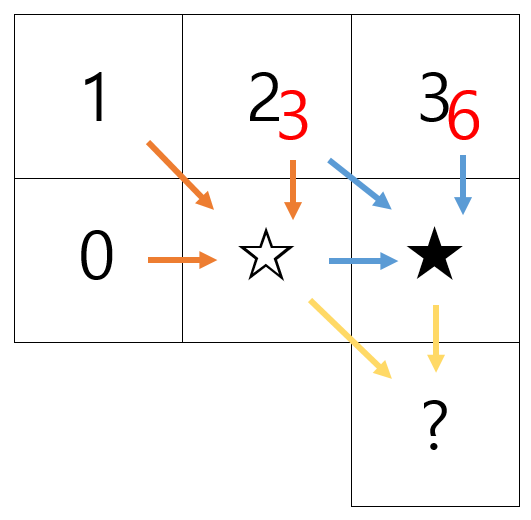
  만약 가장 많은 사탕을 모으는 방법으로 ☆에 도달하고,
  마찬가지로 가장 많은 사탕을 모으는 방법으로로 ★에 도달했다면,
  ☆와 ★ 중 더 많은 사탕을 모은 곳에서 ?로 가는 게 가장 많은 사탕을 모으는 방법입니다.

정답

N,M = list(map(int,input().split(' ')))
#미로를 구현합니다
board = []
for _ in range(N):
    board.append(list(map(int,input().split(' ')))) 
# (r+1,c),(r,c+1),(r+1,c+1)로 이동할 수 있다는 건 (x,y)에 (x-1,y),(x,y-1),(x-1,y-1)에서 도달할 수 있다는 걸 의미합니다.
direction = [[-1,0],[0,-1],[-1,-1]]

#모든 미로칸을 순회합니다
for i in range(N):
    for j in range(M):
        lst = [] # 3방향에서 들어오는 값을 비교하기 위해 일시적으로 lst라는 곳에 담아두겠습니다. 해당 변수는 미로칸이 바뀔때마다 초기화됩니다.
        for d in direction:
            id_ = i+d[0]
            jd_ = j+d[1]
            if 0<=id_<N and 0<=jd_<M: #미로를 벗어나지 않는 값들만 고려합니다
                lst.append(board[id_][jd_])
        if lst: #lst속에 값이 존재한다면
            board[i][j] = board[i][j]+ max(lst) #해당 판으로 오면서 모을 수 있는 최대 사탕의 수 = 3가지 경우의 수 중 가장 많은 사탕을 모은 경우 + 해당 판에 놓인 사탕
                
print(board[N-1][M-1])

기타

• 문제가 복잡해질수록 글과 단편적인 그림만으로 설명하는게 어려운 거 같습니다.
  • 문제를 푸는 것보다 설명을 고민하는 데 더 많은 시간을 사용했지만 설명이 만족스럽지 못합니다
• 최댓값을 구할 수 있는 경로를 출력해라고 한다면?
  • 해당 칸마다 최대사탕의 정보와 해당 경로를 함께 저장하게 만들면 됩니다.