백준 1234번: 크리스마스 트리

문제 설명

• https://www.acmicpc.net/problem/1234
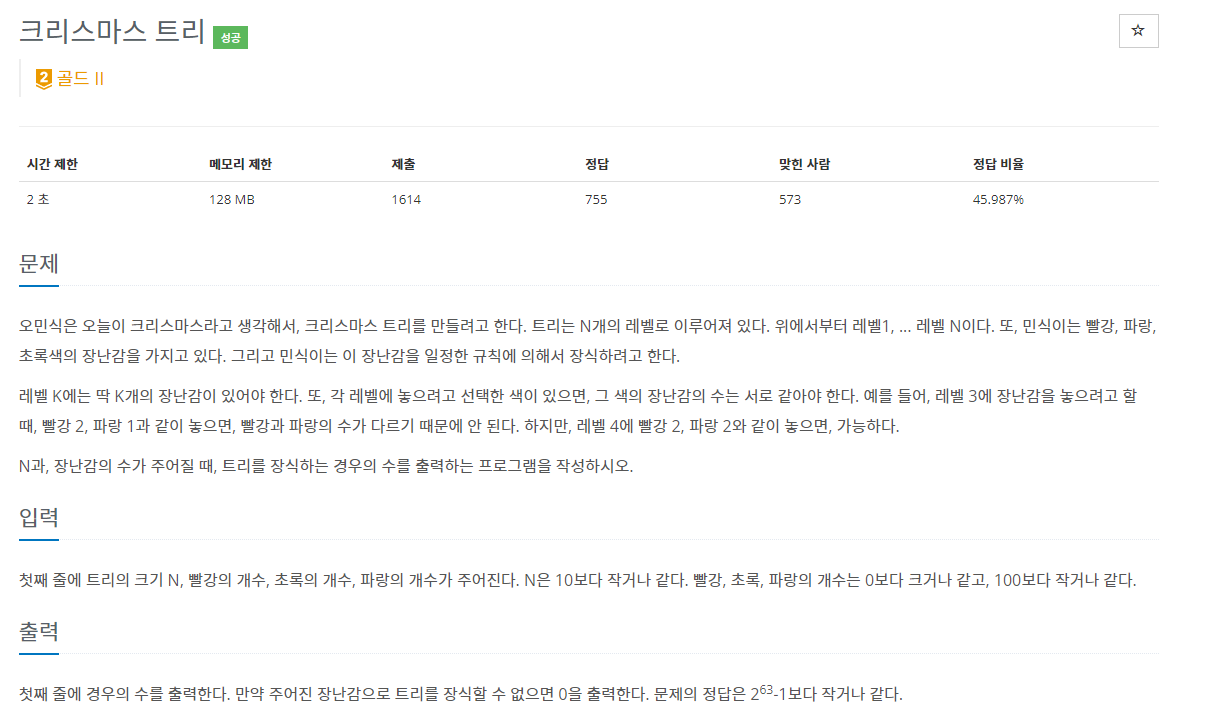
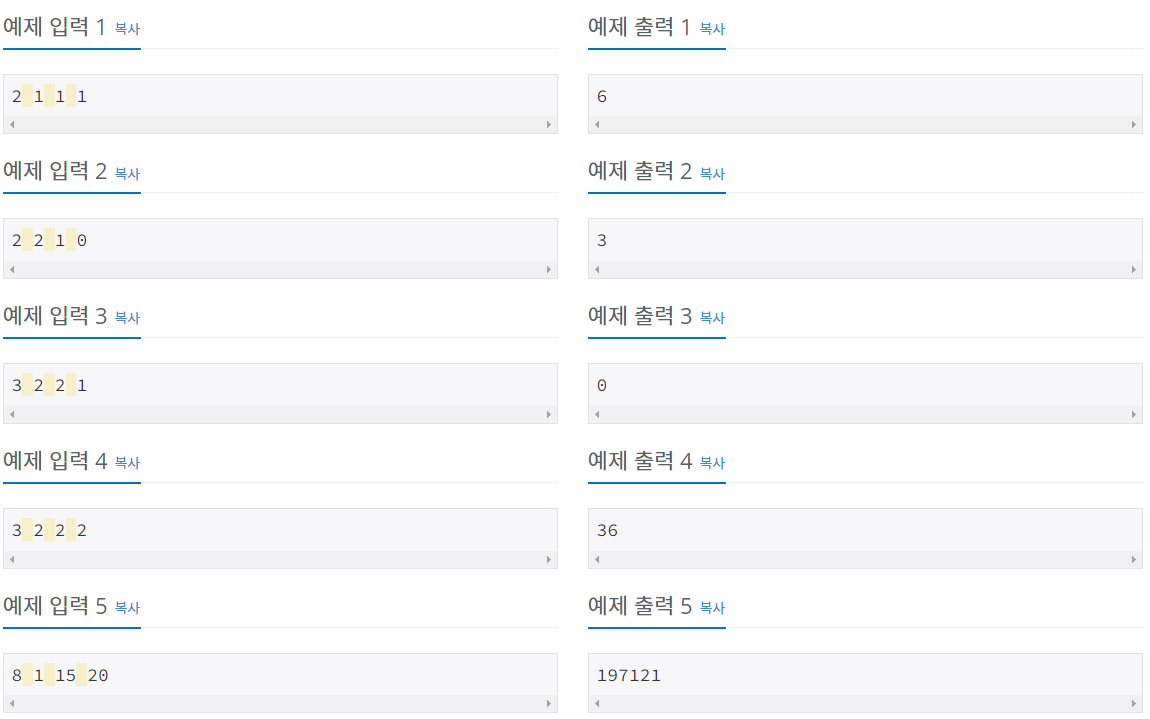
• N단 트리를 만듭니다. 만약 3단 트리를 만든다고 하면 1단에 1개, 2단에 2개, 3단에 3개를 써서 총 6개의 장난감을 사용해 트리를 만든다는 의미입니다.
• 레벨 K에는 딱 K의 장난감만 놓아야 하며 놓인 장난감들의 색의 수가 같아야 합니다.
  이때 장난감 순서가 달라지면 다른 경우의 수로 취급합니다. [R,G]와 [G,R]은 다릅니다.
  색이 같은 장난감은 동일한 장난감으로 취급합니다. 빨간색 장난감 5개로 2층을 만드는 경우의 수는 5C2가 아닌 1 입니다.

접근법

• 저는 이렇게 분기와 조건을 여러 개로 나눠서 답을 구하는 방법 자체가 익숙지 않았습니다. 이러한 풀이가 존재한다는 걸 인지하는게 중요했습니다.

• K단을 꾸미는 방법은 세 가지 입니다. 첫째, 하나의 색만 이용한다. 둘째, 두 가지 색을 이용한다. 셋째, 세 가지 색을 이용한다.
  두 가지 색을 이용하려면 두 가지 색의 장난감 개수가 같아야 하기 때문에 K가 2의 배수여야 가능합니다. K=5면 [R,R,G,G,G]가 되서 개수가 달라짐. K=4면 [R,G,R,G] 가능
  세 가지 색을 이용하려면 세 가지 색의 장난감 개수가 같아야 하기 때문에 K가 3의 배수여야 가능합니다. K=5면 [R,R,G,G,B]가 되서 개수가 달라짐. K=3이면 [R,G,B] 가능

• 경우의 수 (R,G,B가 충분히 많다고 가정해 보겠습니다.)

  • 5단까지 가능한 경우의 수가 dp[5]일 때 dp[6]의 6단을
    • 빨간색으로만 채우는 경우의 수는 어떻게 될까요? dp[5]의 경우의 수와 동일할 겁니다. 이는 빨간색이 아닌 초록색과 파란색에도 동일합니다.
    • 빨간색과 초록색으로 채우는 경우의 수는 어떻게 될까요? dp[5]의 경우의 수에다가 6개 중 3개의 빨간색 자리를 정해주면 되기 때문에 6C3를 곱하면 됩니다.
    • 빨간색과 초록색과 파란색으로 채우는 경우의 수는 어떻게 될까요? dp[5]의 경우의 수에다가 6개 중 2개의 빨간색 자리를 정해주고 남은 4개 중 2개의 파란색 자리를 정해주면 되기 때문에 6C4*4C2를 곱하면 됩니다.

• dp[i][r][g][b]는 빨간색 r개, 초록색 g개, 파란색 b개의 장식품으로 i단 트리를 꾸미는 경우의 수 입니다.

  • 이때 dp[i][r][g][b]중 마지막 i단을 전부 빨간색으로만 꾸미는 경우는 dp[i-1][r-i][g][b]와 동일합니다. 마지막 i단을 r개의 빨간색으로 꾸미려면 1~i-1단까지 사용 가능한 빨간색은 r-i개가 됩니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int R = Integer.parseInt(st.nextToken());
		int G = Integer.parseInt(st.nextToken());
		int B = Integer.parseInt(st.nextToken());
		long[][][][] dp = new long[N+1][R+1][G+1][B+1];
		
		
		for (int i = 0; i <= N; i++) {
			for (int r = 0; r <= R; r++) {
				for (int g = 0; g <= G; g++) {
					for (int b = 0; b <= B; b++) {
						if(i == 0) { // 초기값 세팅
							dp[i][r][g][b] = 1;
							continue;							
						}
                        // i단을 하나의 색으로만 꾸밈
						if(r-i>=0) dp[i][r][g][b] += dp[i-1][r-i][g][b] * 1;
						if(g-i>=0) dp[i][r][g][b] += dp[i-1][r][g-i][b] * 1;
						if(b-i>=0) dp[i][r][g][b] += dp[i-1][r][g][b-i] * 1;
                        // i단을 2개의 색으로 꾸밈
						if(i%2 == 0) {
							int divNum = i/2;
							if(g-divNum>=0 && b-divNum>=0) dp[i][r][g][b] += dp[i-1][r][g-divNum][b-divNum]*comb(i,divNum);
							if(r-divNum>=0 && b-divNum>=0) dp[i][r][g][b] += dp[i-1][r-divNum][g][b-divNum]*comb(i,divNum);
							if(r-divNum>=0 && g-divNum>=0) dp[i][r][g][b] += dp[i-1][r-divNum][g-divNum][b]*comb(i,divNum);
						}
                        // i단을 3개의 색으로 꾸밈
						if(i%3 == 0) {
							int divNum = i/3;
							if(r-divNum>=0 && g-divNum>=0 && b-divNum>=0) dp[i][r][g][b] += dp[i-1][r-divNum][g-divNum][b-divNum]*comb(i,divNum) * comb(i-divNum,divNum);
						}
					}
				}
			}
		}
		System.out.println(dp[N][R][G][B]);
	}
	public static int comb(int n, int r) {
		return factorial(n)/(factorial(r)*factorial(n-r));
	}
	public static int factorial(int x) {
		if(x == 1) return 1;
		return x*factorial(x-1);
	}
}