문제 설명
01 knapsack이라는 정형화된 알고리즘 문제입니다.
접근법
- N의 크기가 100으로 완전탐색으로 풀면 시간초과가 발생합니다.
배낭의 남은 무게를 기준으로 접근해야 합니다.- 현재 남은 무게가 i일 때 각 물건 j는 "내가 가방에 들어갔을 때 가치가 더 커지는가"를 생각합니다.
- 배낭의 남은 무게가 7kg 일 때 3kg의 물건은 "내 가치 + (7-3)kg로 만들수 있는 최고의 가치"와 "이전에 7kg으로 만들었던 최고의 가치"를 비교합니다.
- 각 dp에는 해당 무게로 담을 수 있는 최고의 가치가 기록되어 있습니다.
무거운 곳부터 탐색해야 하는 이유
- 잘못된 값이 덮어씌워지기 때문입니다.
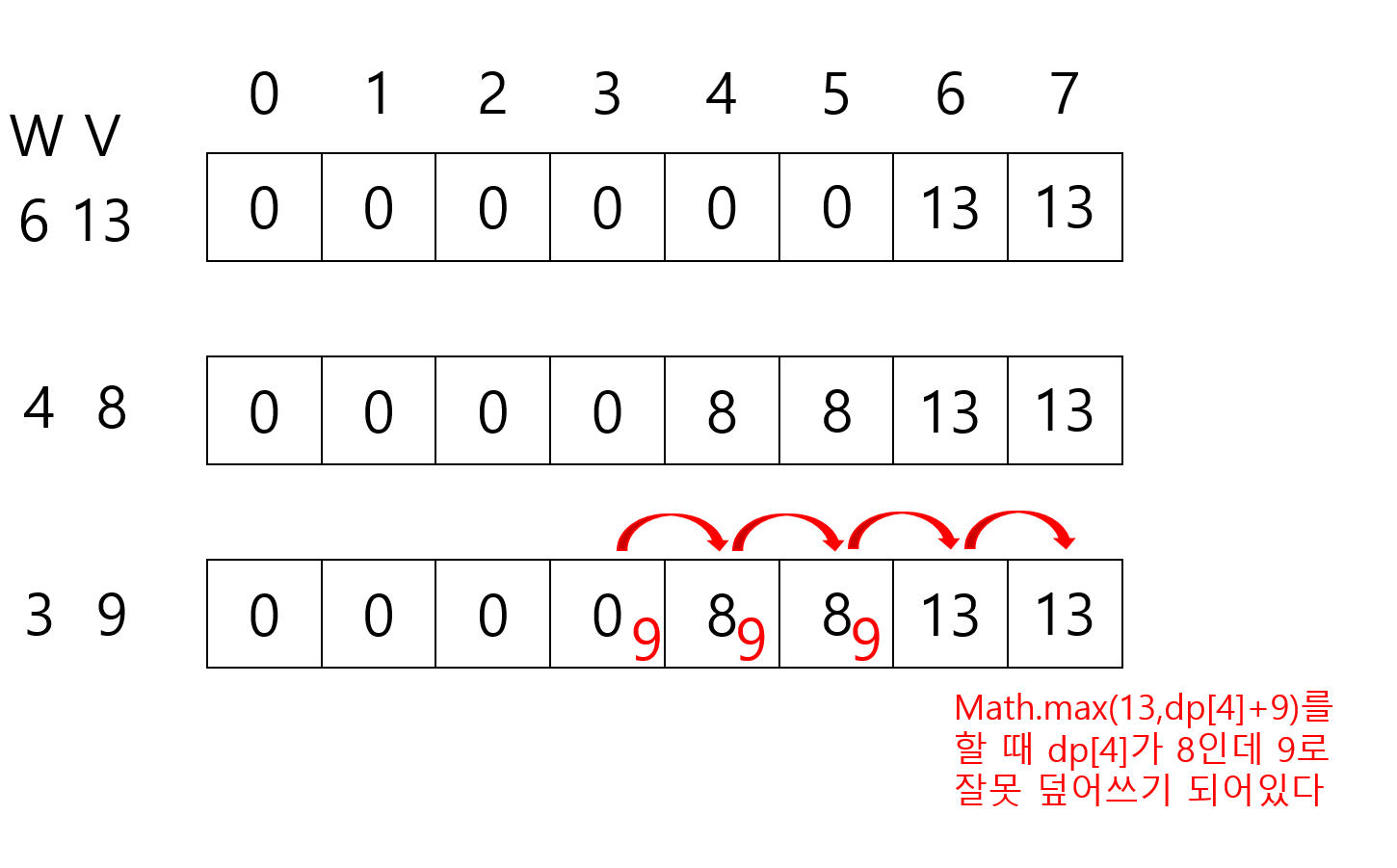
- 3의 짝궁은 어차피 7보다 낮은 숫자이기 때문에 7부터 아래로 갱신해도 아무런 문제가 없습니다.
정답
import java.util.*;
public class Main {
static class material{ // 물건의 무게와 가치를 담기 위한 클래스
int W,V;
public material(int w, int v) {
super();
W = w;
V = v;
}
@Override
public String toString() {
return "material [W=" + W + ", V=" + V + "]";
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringTokenizer st = new StringTokenizer(sc.nextLine()," ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
material[] M = new material[N]; // 물건을 담을 배열
for (int i = 0; i < N; i++) {
st = new StringTokenizer(sc.nextLine()," ");
M[i] = new material(Integer.parseInt(st.nextToken()),Integer.parseInt(st.nextToken()));
}
int[] dp = new int[K+1]; // 여유공간이 0일때부터 K일때까지를 나타내는 dp배열
dp[0] = 0;
for (int j = 0; j < N; j++) { // 물건
for (int i = K; i >= M[j].W; i--) { // 남은 무게
if(i-M[j].W<0)continue; // 여유공간보다 물건이 더 무거우면 패스
dp[i] = Math.max(dp[i],dp[i-M[j].W]+ M[j].V); //
//i = 7, j물건의 무게 = 3, j물건의 가치 = 6이라고 할 때
//이전에 구한(==다른j로 구한) 7로 채울 수 있는 최댓값과 현재 j를 넣었을 때의 값을 비교합니다
//j를 넣었을 때의 가치는 'j의 가치 + (i-j의 무게)일때 최적의 가치' 입니다
}
}
// System.out.println(Arrays.toString(dp));
System.out.println(dp[K]);
}
}기타
틀렸던 이유
- 우선 dp의 점화식부터 설계하지 못했다. 설계는 고사하고 비슷한 방식으로 접근조차 못했다.
- 남은 무게를 사용한다는 개념 자체가 없었다.
- 인터넷에 있는 2차원 배열 풀이의 경우 이해가 잘 안됐다.
- j번째 물건을 넣을 때(j물건의 무게는 jw) i-jw번째 값을 가져와야 한다는 건 이해가 됐는데
- 어떤 row(물건)의 i-jw값을 채택해야 하는지를 잘 모르겠다. 내 개념으로는 각 row에서의 i-jw값을 모두 비교한 뒤 최댓값을 가져와야 할 거 같다.
- 아마 누적탐색을 해서 꼭 j번째 최댓값이 j의 무게가 아니어도 된다는 부분을 잘 이해하지 못해서인거 같다.
처음 설계한 코드의 반례
1 2
1 3
가방에 2kg의 여유무게가 있고 [1kg,3원]의 물건이 있을 때
물건은 하나씩만 존재하기 때문에 1kg물건을 1번 담고 1kg의 빈 공간을 남긴 3원의 결과가 나와야 하는데
제 알고리즘은 이를 고려하지 못하고 1kg물건을 2번 담아 6원의 결과가 나왔습니다.

