백준 13325번: 이진 트리

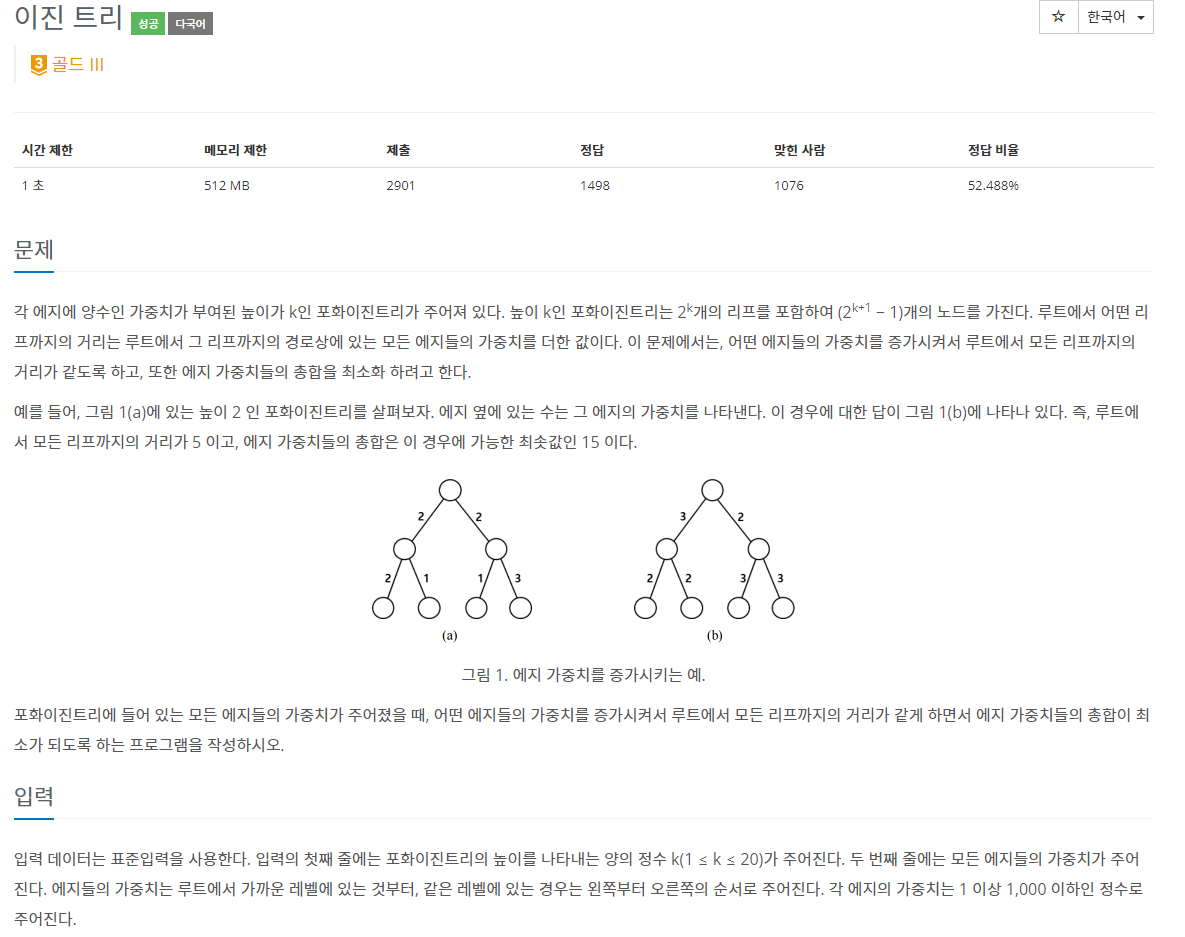
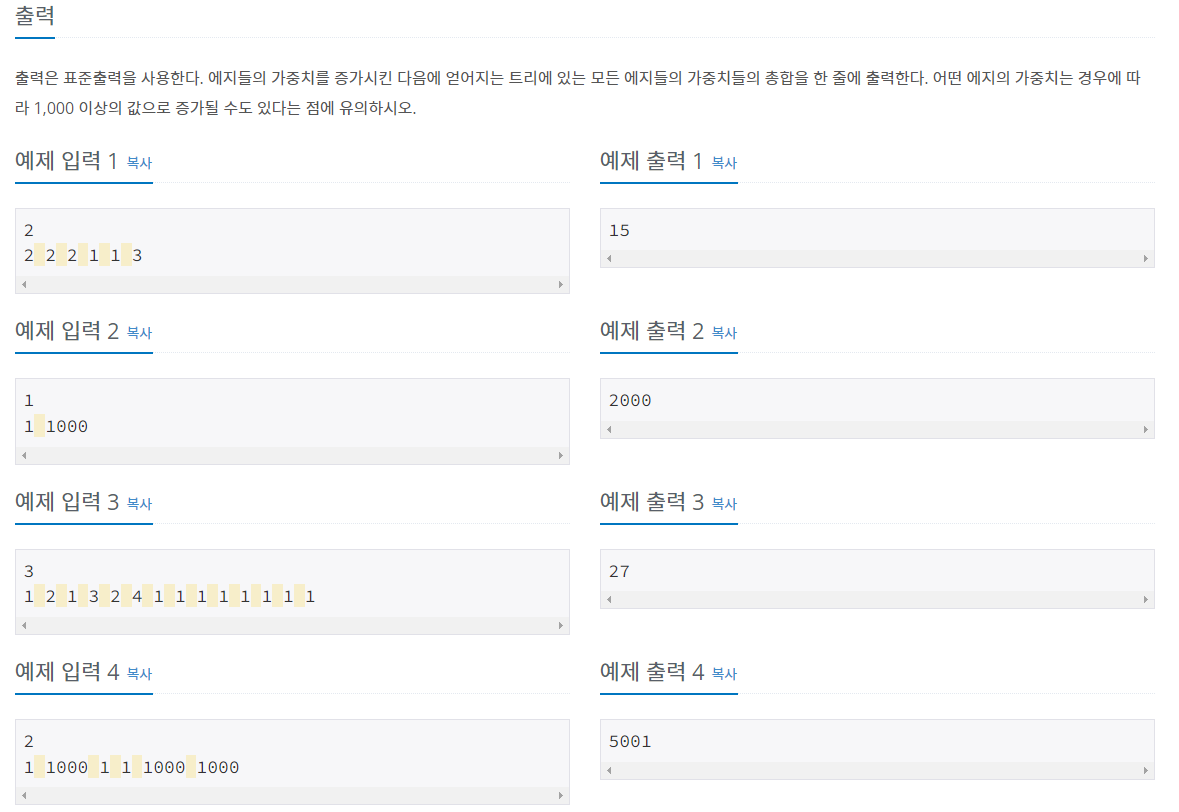
문제 설명

• https://www.acmicpc.net/problem/13325
• 루트부터 리프까지의 거리가 같게 하면서 거리의 총합이 최소가 되도록 만들 때 그 거리의 총합을 구하는 문제입니다.

접근법

• 리프노드부터 i노드까지 거리를 dp[i]로 나타냈습니다.
  • dp[i]는 자신의 왼쪽자식과 오른쪽자식 중 더 먼 거리를 가지게 됩니다.
• dp가 누적값이기 때문에 자식의dp값만큼을 빼줘야 간선 하나의 값이 나옵니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	static long answer = 0;
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));		
		int K = Integer.parseInt(br.readLine());
		int N = (int)(pow(K+1)-1);
		int[] arr = new int[N];
		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 1; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		
		int[] dp = new int[N]; // i노드까지의 누적계산
		// 리프노드부터 탐색
		for (int i = K; i > 0; i--) {
			fillDpArray(i,N,arr,dp);
		}
		System.out.println(answer);
	}
	
	public static void fillDpArray(int x,int N,int[] arr , int[] dp) {
		for (int i = pow(x)-1; i < pow(x+1)-1; i+=2) { // 2칸씩 증가
			// i랑 i+1중 누가 더 큰지
			int maxVal = Math.max(arr[i+1]+childDpVal(i+1,N,dp), arr[i]+childDpVal(i,N,dp));
			dp[i] = maxVal;
			dp[i+1] = dp[i];
			// dp는 누적이기 때문에 자식을 빼줌
			answer += (dp[i] - childDpVal(i,N,dp));
			answer += (dp[i+1] - childDpVal(i+1,N,dp));
		}
		// dp확인
//		System.out.println(Arrays.toString(dp));
	}
	
	public static int childIdx(int x, int N) {
		if((x+1)*2-1 < N) return ((x+1)*2)-1;
		return -1;
	}
	
	public static int childDpVal(int idx, int N, int[] dp) {
		if(childIdx(idx,N) == -1) return 0;
		return dp[childIdx(idx,N)];
	}

	public static int pow(int x) {
		return (int) (Math.pow(2, x));
	}
}