백준 1563번: 개근상

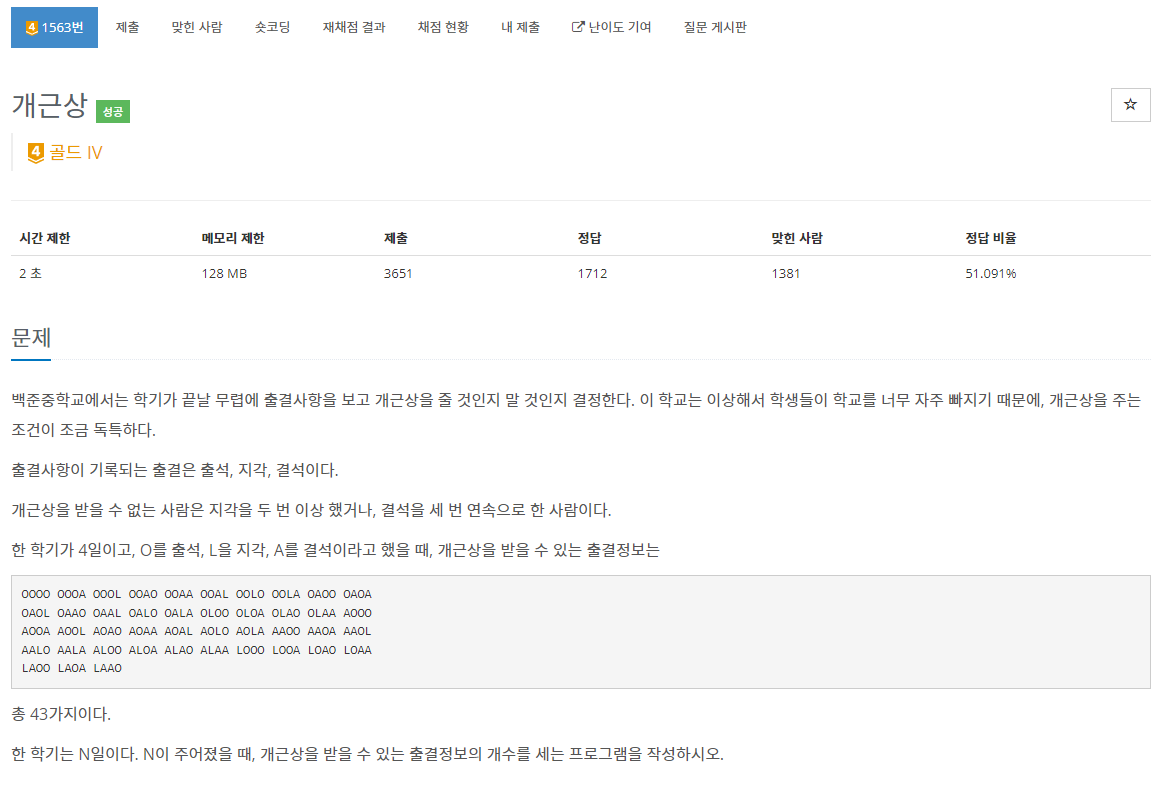
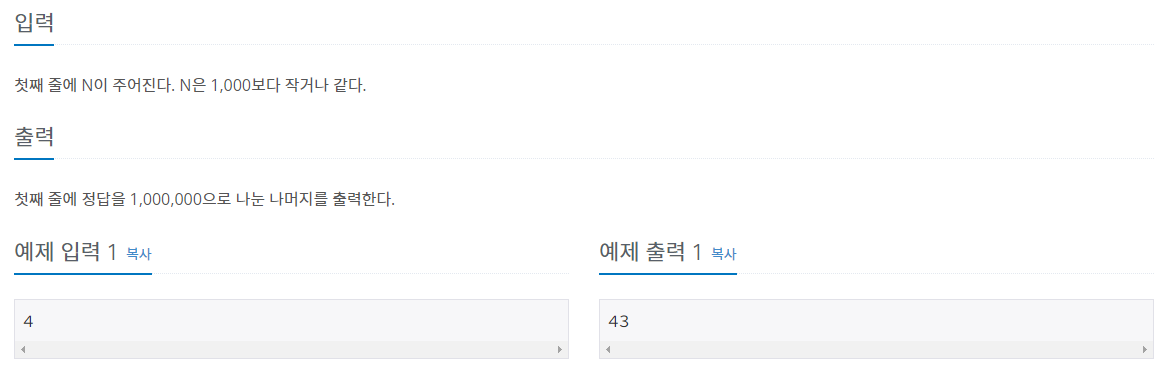
문제 설명

• https://www.acmicpc.net/problem/1563
• O,L,A로 이루어진 길이가 N인 문자열이 있습니다. 만들어진 문자열은 L이 2개 이상이거나 3개 이상의 연속된 A가 존재하면 안됩니다. 조건을 만족하는 문자열 개수를 구하면 됩니다.

접근법

• i번째를 알기 위해서는 직전에 A가 몇번 연속했는지, 해당 문자열에 L이 몇개 사용됐는지를 알고 있어야 합니다. 문자열 경우의 수를 모두 고려하기에는 3^1000으로 값이 너무 큽니다.
• dp[문자열의 길이][연속된 A의 개수][L이 포함된 횟수]를 나타내는 3차원 배열을 활용했습니다. (A와 L의 개수는 i번째 문자까지 카운팅 해 계산한 값입니다.)
  • dp[i][0][0]: 연속된 A가 없기 때문에 i번째 값이 A가 아닙니다. 사용된 L이 0이기 때문에 i번째 값이 L이 아니며 이전에 L이 사용된 적 없어야 합니다.
    • dp[i-1][0][0]: 직전이 O, 현재 O를 놓습니다.
    • dp[i-1][1][0]: 직전이 A, 현재 O를 놓습니다.
    • dp[i-1][2][0]: 직전과 그 전이 모두 A, 현재 O를 놓습니다.
  • dp[i][0][1]: 연속된 A가 없기 때문에 i번째 값이 A가 아닙니다. 사용된 L이 1이라는 건 이번에 L이 오거나, 이전에 L을 썼고 이번에 L이 아닌 다른 값이 올 수 있습니다.
    • dp[i-1][0][0]: 직전이 O, 현재 L을 놓습니다.
    • dp[i-1][1][0]: 직전이 A, 현재 L을 놓습니다.
    • dp[i-1][2][0]: 직전과 그 전이 모두 A, 현재 L을 놓습니다.
    • dp[i-1][0][1]: 앞에서 L을 사용함, 직전이 A가 아님, 현재 O를 놓습니다.
    • dp[i-1][1][1]: 앞에서 L을 사용함, 직전이 A, 현재 O를 놓습니다.
    • dp[i-1][2][1]: 앞에서 L을 사용함, 직전과 그 전이 모두 A, 현재 O를 놓습니다.
  • dp[i][1][0]: 연속된 A가 하나여야 하기 때문에 이번에 반드시 A를 놓아야 합니다. L을 사용한적 없어야 합니다.
  • dp[i][1][1]: 연속된 A가 하나여야 하기 때문에 이번에 반드시 A를 놓아야 합니다. 이전에 L을 사용했어야 합니다.
  • dp[i][2][0]: 연속된 A가 둘이어야 하기 때문에 이전에 A를 놓았고 이번에도 A를 놓아야 합니다. L을 사용한적 없어야 합니다.
  • dp[i][2][1]:연속된 A가 둘이어야 하기 때문에 이전에 A를 놓았고 이번에도 A를 놓아야 합니다. 이전에 L을 사용했어야 합니다.

정답

import java.util.*;
import java.io.*;
import java.math.*;

public class Main {
	public static void main(String[] args) throws Exception{
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int[] arr = new int[N+1];
		int[][][] dp = new int[N+1][3][2]; // [시간][연속A][지각]
		dp[1][0][0] = 1;
		dp[1][1][0] = 1;
		dp[1][0][1] = 1;
		int divNum = 1_000_000;
		for (int i = 2; i <= N; i++) {
			dp[i][0][0] = (dp[i-1][0][0] + dp[i-1][1][0] + dp[i-1][2][0])%divNum;
			dp[i][0][1] = (dp[i-1][0][0] + dp[i-1][1][0] + dp[i-1][2][0] + 
					dp[i-1][0][1] + dp[i-1][1][1] + dp[i-1][2][1])%divNum;
			dp[i][1][0] = (dp[i-1][0][0])%divNum;
			dp[i][1][1] = (dp[i-1][0][1])%divNum;
			dp[i][2][0] = (dp[i-1][1][0])%divNum;
			dp[i][2][1] = (dp[i-1][1][1])%divNum;			
		}
		int answer = (dp[N][0][0] + dp[N][0][1] + dp[N][1][0] + dp[N][1][1] + dp[N][2][0] + dp[N][2][1])%divNum;
		System.out.println(answer);
		
	}
	
}