백준 15966번: 군계일학

문제 설명

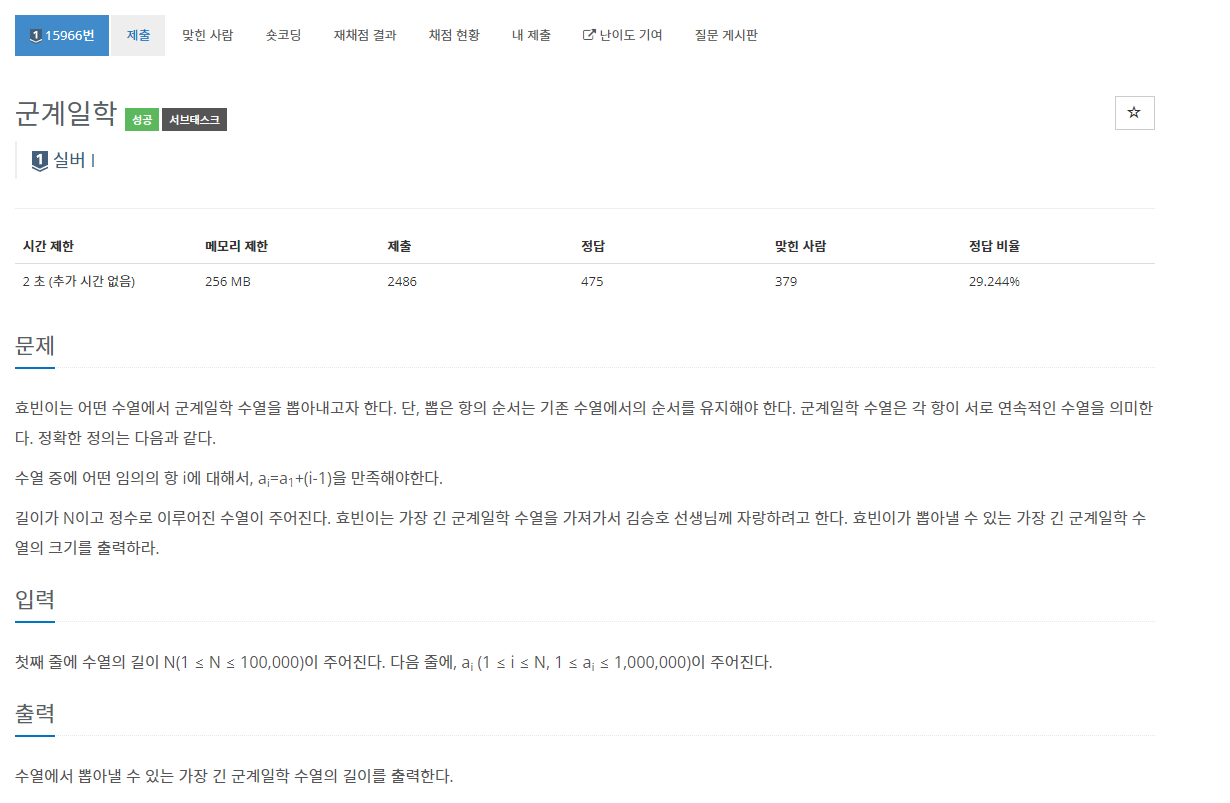
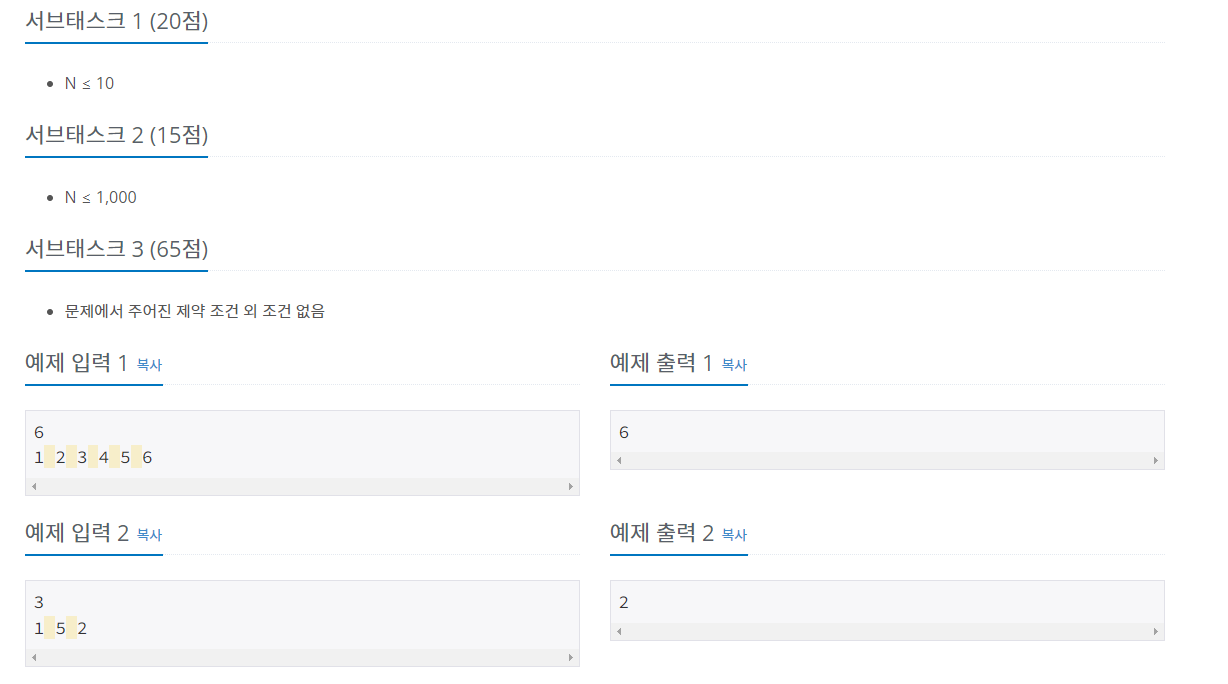
• https://www.acmicpc.net/problem/15966
• 1씩 증가하는 부분수열 중 길이가 가장 긴 배열의 길이를 구하는 문제입니다.

접근법

• dp배열을 dp[i]는 원소i를 마지막 값으로 하는 부분수열의 최대길이로 정의합니다.
  dp[6]은 6을 마지막 원소로 하는 부분수열의 최대길이로 dp[5]+1이 됩니다.
  6을 마지막 원소로 하는 부분수열은 {1,2,3,4,5,6},{2,3,4,5,6},{3,4,5,6},{4,5,6},{5,6},{6}이 될 수 있습니다.

• dp문제는 배열을 어떻게 정의하는지가 중요합니다.
  지금까지 입력으로 주어지는 원소가 N개일 때 dp의 길이는 N인 경우가 많았습니다.
  하지만 이번 문제는 '가능한 원소의 최댓값'만큼의 길이를 갖는 dp배열을 설계해야 합니다.

정답

import java.util.*;
import java.io.*;
import java.math.*;

public class Main {
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];
		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 0; i < arr.length; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		int[] dp = new int[1_000_001];
		int maxVal = Integer.MIN_VALUE;
		for (int i = 0; i < N; i++) {
			int num = arr[i];
			dp[num] = Math.max(dp[num-1]+1, 1);
			maxVal = Math.max(dp[num],maxVal);
		}
		System.out.println(maxVal);
	}
}