백준 17213번: 과일 서리

문제 설명

• N개의 종류에서 M개를 선택하는 경우의 수를 구하는 문제입니다. 이때 N개의 종류는 각각 최소 1번 이상 선택되어야 합니다.
• https://www.acmicpc.net/problem/17213

접근법

• 중복조합으로도 문제 해결이 가능합니다.
  • $nHr = (n-1+r)C(r)$
• 동적 계획법으로도 문제를 해결할 수 있습니다.
  • n=1일 때 m이 아무리 커도 선택할 수 있는 경우의 수는 1입니다.
  • n=2일 때 dp[i][j] = j-1입니다.
  • n=k일 때 dp[i][j] = dp[i-1][0]+dp[i-1][1]+...dp[i-1][j-1] 입니다.
  • 모든 과일을 적어도 하나 선택해야 하기 때문에 j<N일 때 dp[i][j]는 0이고 j=N일 때 dp[i][j]는 1입니다.

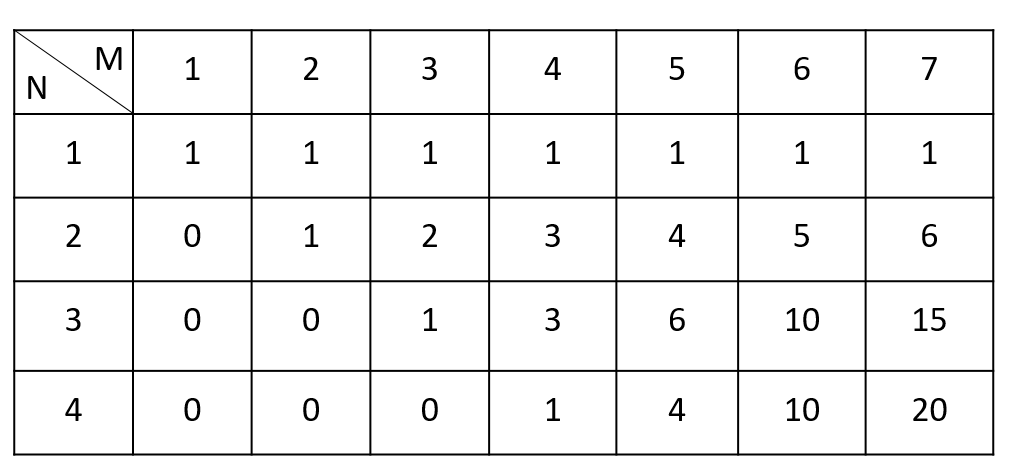
dp[i][j] = dp[i-1][0]+dp[i-1][1]+...dp[i-1][j-1]인 이유를 살펴보겠습니다.

• M이 동일할 때 N이 1개 증가한 상황은 어떤 걸까요? N=3에서 N=4가 됐다는 건 A,B,C 과일을 훔치던 상황에서 A,B,C,D 과일을 훔쳐야 되는 상황으로 변경된 겁니다. 이때 M의 개수가 동일하기 때문에 새롭게 추가된 D의 개수를 기준으로 생각해보면 됩니다.
  • 만약 D를 1개 훔쳤다면 우리는 A,B,C를 총 M-1개 훔쳐야 합니다.
  • 만약 D를 2개 훔쳤다면 우리는 A,B,C를 총 M-2개 훔쳐야 합니다.
  • 만약 D를 x개 훔쳤다면 우리는 A,B,C를 총 M-x개 훔쳐야 합니다.

이러한 규칙을 옮긴 게 바로 위 점화식입니다. dp[i-1][0]은 D를 M개 훔쳐 A,B,C를 총 0개 훔치는 경우, dp[i-1][1]은 D를 M-1개 훔쳐 A,B,C를 총 1개 훔치는 경우, dp[i-1][j-1]은 D를 1개 훔쳐 A,B,C를 총 M-1개 훔치는 경우입니다.

정답

import java.util.*;

public class Main {
	public static void main(String[] args) throws Exception{
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int M = sc.nextInt();
		int[][] dp = new int[N][M];
		Arrays.fill(dp[0], 1);
		for (int i = 1; i < N; i++) {
			for (int j = i; j < M; j++) {
				int sumVal = 0;
				for (int k = 0; k <= j-1; k++) {
					sumVal += dp[i-1][k];
				}
				dp[i][j] = sumVal;
			}
		}
		System.out.println(dp[N-1][M-1]);
	}
}