백준 2293번: 동전 1

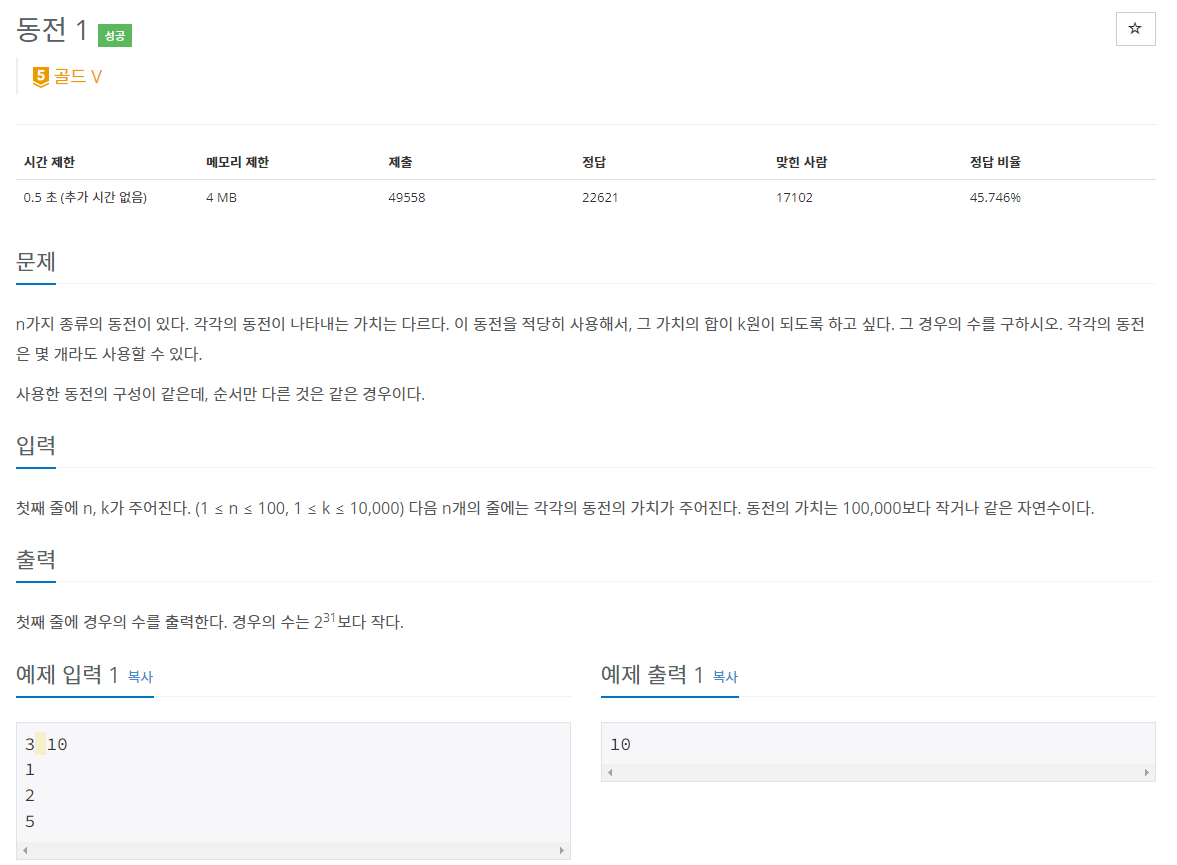
문제 설명

• https://www.acmicpc.net/problem/2293
• 주어진 n개의 동전을 조합해 k를 만드는 경우의 수를 구하는 문제입니다.

접근법

• 2차원 배열을 활용할 수 있습니다.
  dp[i][j]는 i개의 동전을 사용해 숫자 j를 만드는 경우의 수 입니다.

• dp[i][j] = dp[i-1][j] + dp[i][j-coin]입니다. (coin은 i번째 동전의 가치)

  예제 케이스를 예로들면 dp[2][10] = dp[2-1][10] + dp[2][10-5] 라는 식이 만들어질 수 있습니다.
  dp[2-1][10]는 동전5를 사용하지 않고 동전1과 동전2만 사용햐 10을 만드는 경우의 수 입니다.
  dp[2][10-5]는 동전1, 동전2, 동전5를 사용해 5를 만드는 경우의 수 입니다.
  3가지 동전을 이용해 10을 만드는 경우의 수는 3가지 동전을 이용해 5를 만든 뒤 그 경우의 수에 동전5를 추가하면 됩니다. 그렇기 때문에 경우의 수는 그대로 유지됩니다.

  • 1,2,2로 5를 만들었다면 여기에 동전5를 추가해 1,2,2,'5'로 10을 만들 수 있습니다.

• 초기값 설정

  • 첫 행의 값은 첫번째 동전만 사용해 만들 수 있는 경우의 수 입니다. 동전값으로 나누어떨어지는 숫자만 만들 수 있으며, 그 경우의 수는 항상 한 가지 입니다. 첫 동전이 3이라면 3,6,9,... 의 값을 만들 수 있습니다. 이때 가능한 경우의 수는 모두 한 가지 입니다.
  • 첫 열의 값을 1로 설정해 두면 편리합니다.
    그 이유는 dp[i][j] = dp[i-1][j] + dp[i][j-coin]에서 dp[i][j-coin]를 구할 때 유용하기 때문입니다.
    동전k로 숫자 k를 만드는 경우의 수는 반드시 하나 존재합니다. 동전의 값이 2라면 해당 동전으로 합이 2인 수를 반드시 1개 만들 수 있습니다. 이때 j=2면 dp[i][j-coin]은 dp[i][0]이 되기 때문입니다.

정답

import java.util.*;
import java.io.*;

public class Main {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int n =Integer.parseInt(st.nextToken());
		int k =Integer.parseInt(st.nextToken());
		int[] arr = new int[n];
		for (int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		int[][] dp = new int[n][k+1];

		for (int i = 0; i < k+1; i++) {
			if(i%arr[0] == 0) {				
				dp[0][i] = 1;
			}
		}
		
		// dp[i][j] = dp[i-1][j] // i번째 동전을 사용하지 않고 j원을 만드는 경우의 수
		//             + dp[i][j-coin] // j-coin원을 만드는 경우의 수와 j원을 만드는 경우의 수는 동일합니다.
		// 이때 x원짜리 동전을 활용해 x원을 만드는 경우는 1입니다.
		for (int i = 0; i < n; i++) {
			dp[i][0] = 1;
		}
		
		for (int i = 1; i < n; i++) {
			int coin = arr[i];
			for (int j = 0; j < k+1; j++) {
				dp[i][j] = dp[i-1][j] + (j-coin>=0?dp[i][j-coin]:0); 
			}
		}
		System.out.println(dp[n-1][k]);
		for (int i = 0; i < dp.length; i++) {
			System.out.println(Arrays.toString(dp[i]));
		}

	}

}