백준 2533번: 사회망 서비스(SNS)

문제 설명

• https://www.acmicpc.net/problem/2533
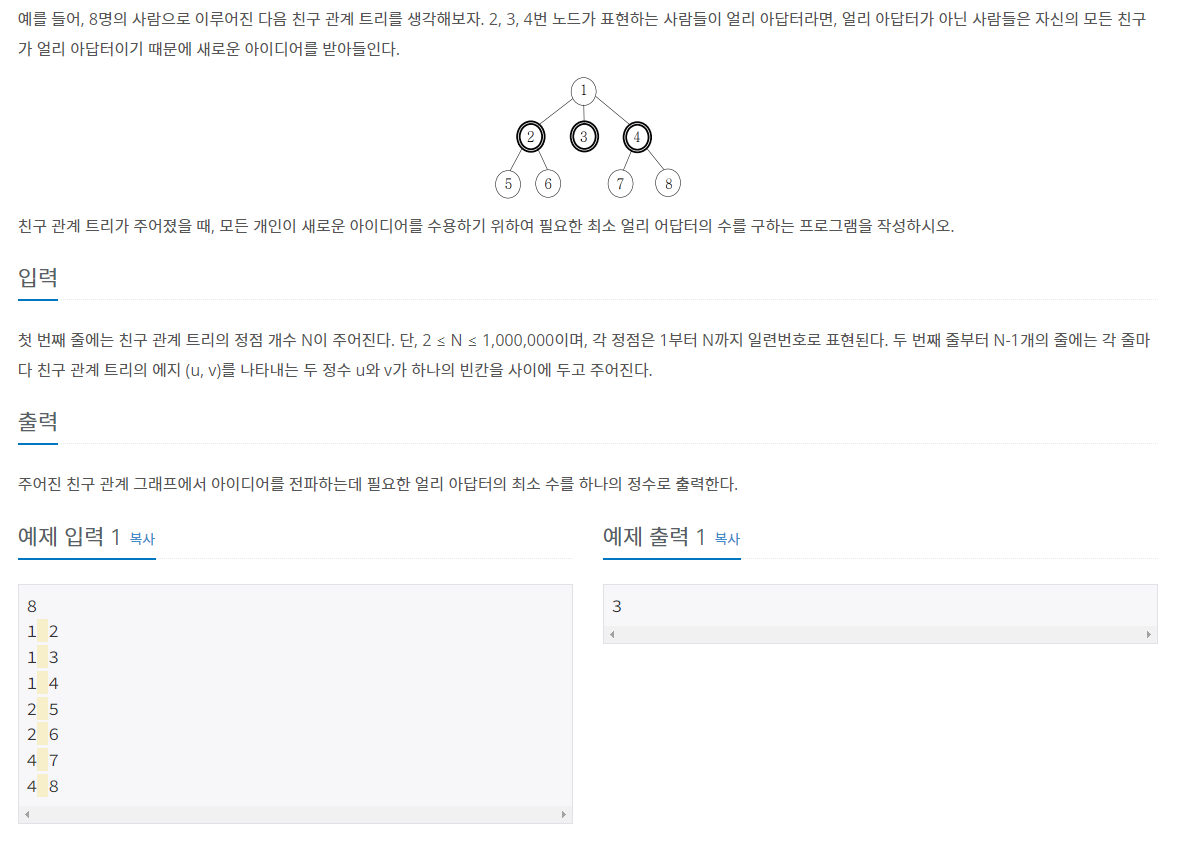
• 어떤 노드를 선택하면 해당 노드와 연결된 노드들은 모두 효과를 봅니다.
  트리의 모든 노드가 효과를 보기 위해 최소 몇 개의 노드를 선택해야 하는지 구하는 문제입니다.

접근법

• 대부분의 DP문제가 그렇지만 처음부터 너무 세세하게 접근하면 더 풀기가 어렵습니다. 이렇게 하면 이런 반례가 있지 않을까? 어떤 구체적인 방법이 있지 않을까? 라는 생각보다는 naive하게 또는 점화식 위주(이전의 값과 지금의 값을 연관짓는)의 생각으로 접근하는 게 더 좋은 경우가 많은거 같습니다.

• 아래 내용이 문제의 핵심입니다.

  • x를 선택하지 않으면 x와 연결된 모든 노드는 반드시 선택해야 합니다.
  • x를 선택하면 x와 연결된 모든 노드는 '선택해도 되고 선택하지 않아도 됩니다'.

• 이를 바탕으로 dp배열에 들어가는 값을 해당 노드까지 고려했을 때 해당 노드 아래로 모두 얼리 어답터가 되기 위해 선택한 최소한의 노드 수라고 정의할 수 있습니다. 그리고 이는 해당 노드를 선택했을 때, 선택하지 않았을 때 두 가지로 나뉠 수 있습니다.
  즉, dp[x][0]은 x를 선택하지 않고 x아래를 모두 얼리 어답터로 만드는 최소 경우의 수, dp[x][1]은 x를 선택하고 x아래를 모두 얼리 어답터로 만드는 최소 경우의 수가 됩니다.
  사실 루트가 정해져 있지 않아 노드 아래라고 표현하기 애매합니다. 하지만 DFS로 계속 다음 값을 탐색한다는 측면에서 트리와 같은 그래프로 생각할 수 있습니다.

• 위와 같이 dp를 정의한 뒤 dp배열을 채우는 방법은 DFS순회를 도는 것입니다. 루트에서부터 자식으로 내려가면서 값을 찾습니다.

• 문제를 풀면서 다음과 같은 내용이 애매했었습니다.

  • root로 지정한 노드가 바뀌어도 되는가? 모든 값을 root로 두고 풀어야 하는거 아닐까? -> 실제로는 depth가 아니라 연결된 형태에 영향을 받기 때문에 상관이 없습니다.
  • BFS를 쓰면 안되는가? -> 안됩니다. BFS는 해당 노드를 탐색하는 시점에 자식들의 dp값을 알지 못합니다. 하지만 DFS는 재귀를 호출하는 부분이 끝난 뒤에는 자식들의 dp값을 알기 때문에 문제를 DFS로 풀어야 합니다.

정답

import java.util.*;
import java.io.*;
import java.math.BigInteger;

public class Main {
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		HashMap<Integer,List<Integer>> graph = new HashMap<Integer,List<Integer>>();
		for (int i = 0; i < N-1; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());

			if(graph.containsKey(a)) {
				graph.get(a).add(b);
			}else {
				List<Integer> temp = new ArrayList<Integer>();
				temp.add(b);
				graph.put(a, temp);
			}
			
			if(graph.containsKey(b)) {
				graph.get(b).add(a);
			}else {
				List<Integer> temp = new ArrayList<Integer>();
				temp.add(a);
				graph.put(b, temp);
			}
		}
		boolean[] v = new boolean[N+1];
		int[][] dp = new int[2][N+1];
        int root = (int)Math.random()*N+1; // 아무 값이나 설정해도 상관없습니다.
		DFS(root,v,graph,dp);

		System.out.println(Math.min(dp[0][root], dp[1][root]));
	}
	
	public static void DFS(int now, boolean[] v, HashMap<Integer,List<Integer>> graph, int[][] dp) {
		v[now] = true;
		// now를 선택안하면 0개 + next모두를 선택했을 때 값
		dp[0][now] = 0;
		// now를 선택하면 1개 + Math.min(next를 선택한다, next를 선택하지 않는다);
		dp[1][now] = 1;

		for (Integer next : graph.get(now)) {
			// 리프 노드는 자신과 연결된 노드가 parent하나밖에 없음
			// parent는 이미 리프노드보다 먼저 방문되었기 때문에 결국 리프노드는 dp[0][now] = 0; dp[1][now] = 1;라는 기본값을 그대로 가짐
			if(v[next]) continue;
			DFS(next,v,graph,dp);
			// 재귀적으로 DFS를 다 수행하고 왔기 때문에 나보다 자식 노드들에 대한 dp가 다 채워져있다.
			dp[0][now] += dp[1][next];
			dp[1][now] += Math.min(dp[0][next], dp[1][next]);
		}
	}
	
}