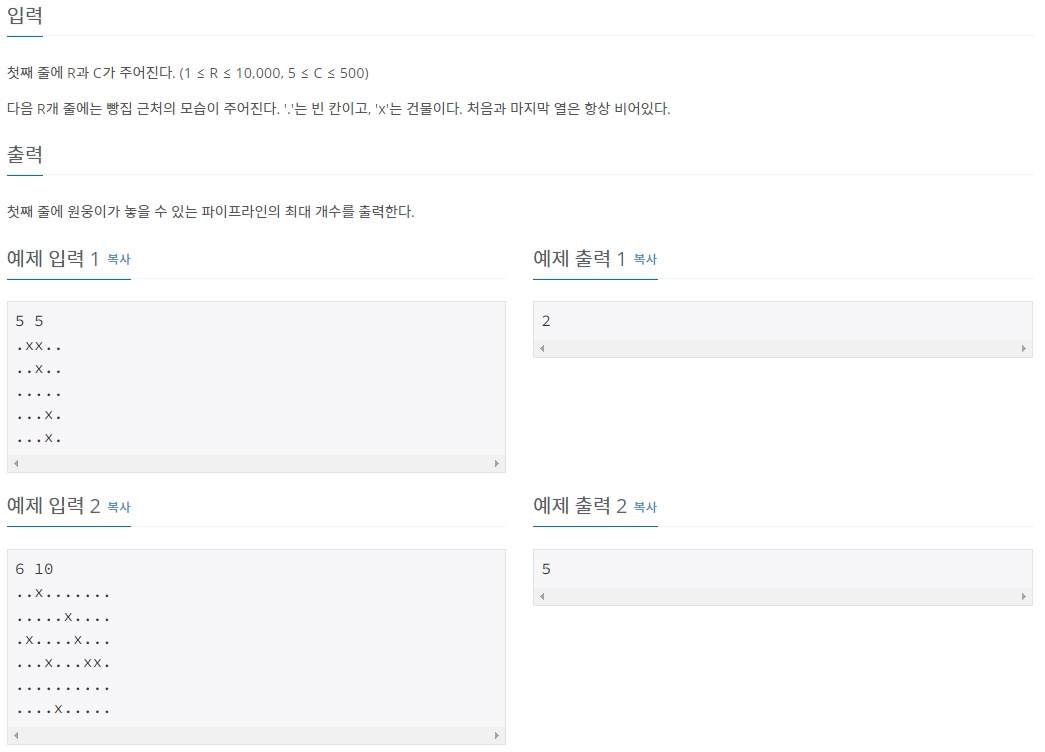
문제 설명
- 가장 왼쪽에서 가장 오른쪽으로 연결할 수 있는 선의 최대개수를 구하는 문제입니다.
- 오직 3가지 움직임(오른쪽 위 대각선, 오른쪽, 오른쪽 아래 대각선)만 허용합니다.
접근법
- 하나의 지점에서 시작해서 도달할 수 있는 경로가 여러개 있다면
반드시 최대한 위로 붙어서 가는 경로를 선택하는 게 유리합니다.
3가지 값중위가 가장 좋은 이유는 0행(위)부터 R-1행(아래) 순서로 탐색을 진행하기 때문입니다.
위로 갈 수 있는데 다른 길을 선택하면 다음 출발주자의 도달 가능성을 해치게 됩니다.
-
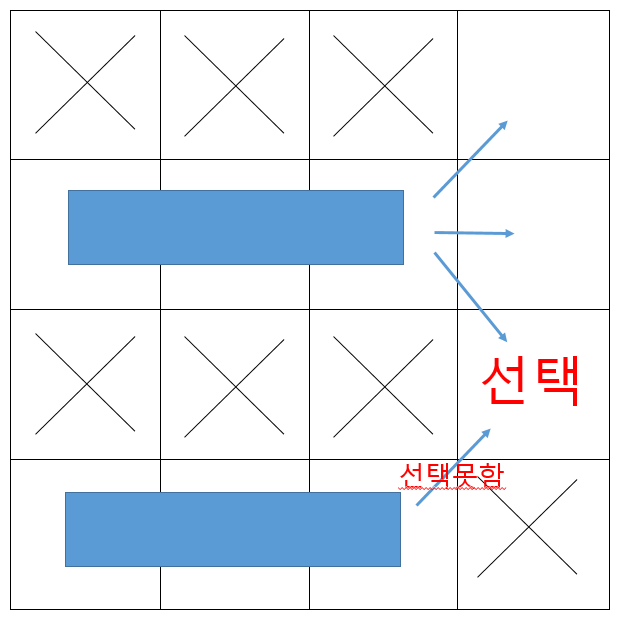
위로 붙어서 가는 선택이 유리하다는 Greedy한 선택을 해야 합니다. -
백트래킹에서 잘못된 경로에 진입해 이전으로 되돌릴 때 지나온 길의 건물을 철거하지 않습니다.
- 다음주자에게 그 길을 선택하지 말라는 의미입니다. (pruning)
- '이 길로 내가 가봤는데 나중에 막다른길이 나오더라고. 그러니깐 넌 일로 가지마' 라는 의미입니다.
-
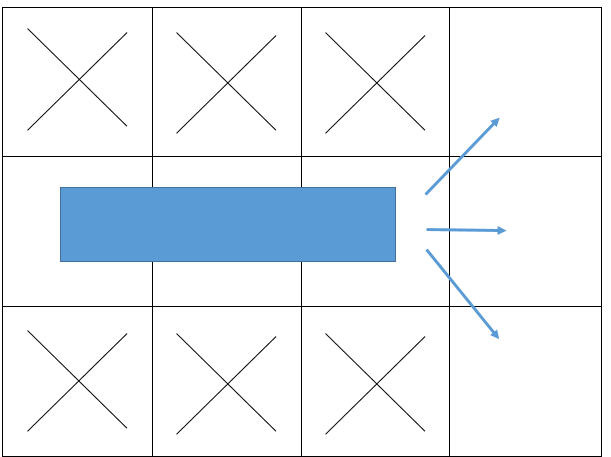
일반적인 백트래킹은 다음과 같은 경우에서 3가지 경로를 모두 탐색합니다.
-
여기에 건물을 철거하는 방식을 선택하면 다음과 같은 결과가 나옵니다.
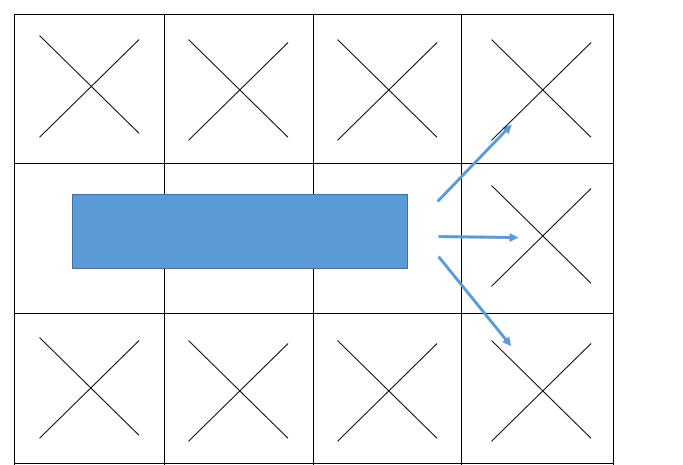
-
반대로 건물을 철거하더라도 일반적인 백트래킹으로는 셋중 어디를 방문했는지 표시를 남길 수 없습니다.
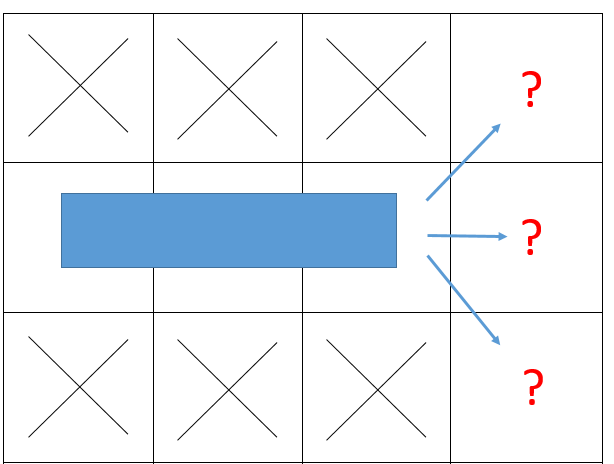
-
즉 우리에게는 같은 출발지에서 최초의 정답이 발생한다면 재귀로 탐색하기로 했던 일정을 모두 취소해야 합니다.
* 아래 코드에서 finished변수의 역할을 보시면 어떤 얘기인지 이해하실 수 있을 겁니다.
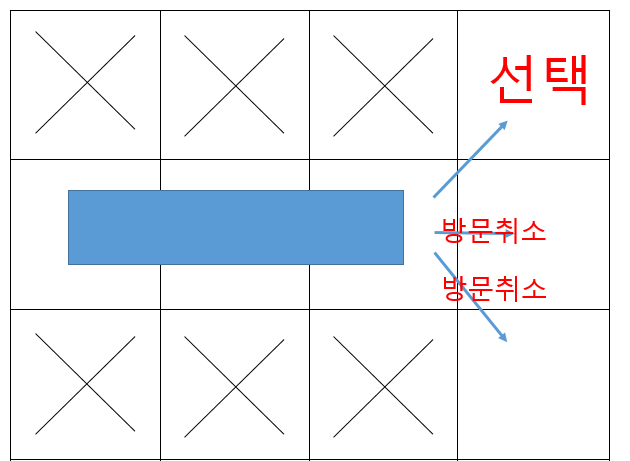
-
주석처리된 부분을 주석해제하면 전체 경로를 탐색하는 과정을 눈으로 볼 수 있습니다. 경로를 쉽게 알아보기 위해 @변수를 사용했지만 문제를 푸실 때에는 그냥 'x'를 넣으면 됩니다.
정답
import java.util.*;
public class Main {
static int R,C,cnt;
static char[][] board;
static int[] dx = {-1,0,1};
static int[] dy = {1,1,1};
static boolean finished;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringTokenizer st = new StringTokenizer(sc.nextLine()," ");
R = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
board = new char[R][C];
for (int i = 0; i < R; i++) {
board[i] = sc.nextLine().toCharArray();
}
//출발지점에서 각각 DFS(백트래킹)을 실행합니다.
for (int i = 0; i < R; i++) {
finished = false;
board[i][0] = '@'; // 눈으로 변화를 확인하기 위해 넣은 코드입니다.
BackT(i,0);
}
System.out.println(cnt);
}
public static void BackT(int x, int y) {
//전체 진행과정을 확인하기 위한 코드입니다.
//System.out.println();
//for (int j = 0; j < board.length; j++) {
// System.out.println(Arrays.toString(board[j]));
//}
//System.out.println();
if(y == C-1) { // 마지막 행에 도달했다면 경로가 완성된 것입니다.
finished = true; //해당 출발지에서 도달가능한 경로를 찾았기 때문에
// 재귀예정인 탐색을 모두 취소하게 합니다.
cnt++;
return;
}
for (int i = 0; i < 3; i++) {
int nx = x + dx[i];
int ny = y + dy[i]; //dy값은 다 1이기 때문에 y+1을 해도 상관없습니다.
// 답이될수 없는 경우의 수는 가지치기(pruning)합니다.
if(nx<0 || nx>=R || ny>=C || board[nx][ny] == 'x' || board[nx][ny] == '@') continue;
// 해당 출발지에서 갈 수 있는 최적경로가 등장했다면 더 이상 재귀적인 탐색을 하지 않습니다.
if(finished) continue;
// 여기까지 왔다는 건 아직 최적의 경로가 등장하지 않았다는 뜻입니다.
board[nx][ny] = '@';
BackT(nx,ny);
}
}
}
기타
-
finished변수를 통해 다음과 같은 경우를 만들었다고 비유할 수 있습니다.
1등만 상금을 주는 퀴즈대회에 참여했습니다.
1등이 아직 등장하지 않았다면 열심히 문제를 풀겠지만,
1등이 등장했으면(finished가 true면) 문제를 열심히 풀 필요가 없게됩니다. -
문제가 풀리지 않아 링크에 있는 원 대회의 데이터를 가져와 틀린 부분을 찾았습니다.
15 15
.xxxxxxxxxx....
...x.......xxx.
...x.......x...
..xx.......xx..
...x........xx.
.x.x......x.x..
...x......xx...
.x.x....xxx....
.x....x.x......
.x.....xx.x....
.x..x.xx.......
.....xx........
....x..........
......x........
...............
정답 4 -
백트래킹이 아니라
우상단>중간>우하단으로 하나만 선택하게 하면 다음의 반례에 막힙니다.5 7
.x...x.
.x...x.
.x.....
.......
.......
정답 2

