백준 7570번: 줄 세우기

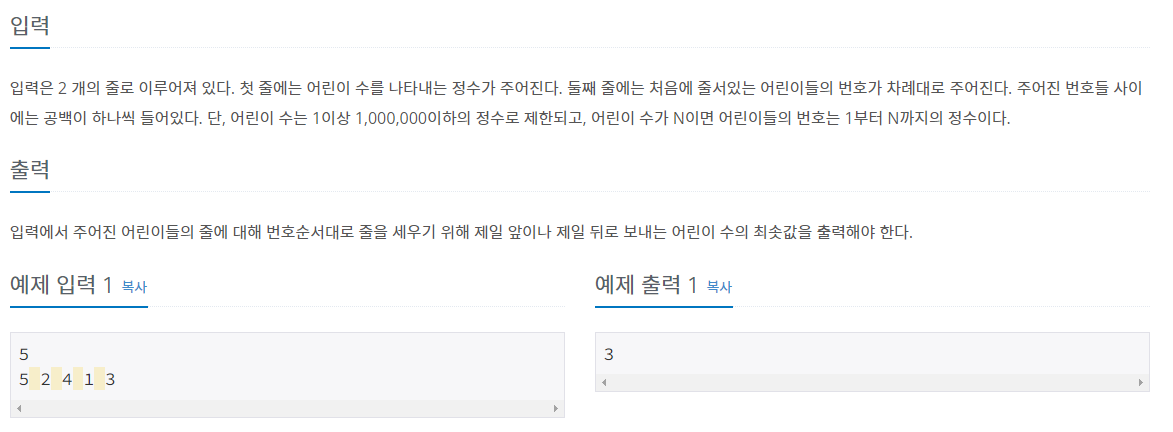
문제 설명

• https://www.acmicpc.net/problem/7570
• 숫자를 가장 앞으로 보내거나 가장 뒤로 보낼 수 있습니다.
  이를 통해 숫자를 오름차순으로 정렬하려 할 때 최소 움직임을 구하는 문제입니다.

접근법

• 움직여야 하는 값을 찾는 것보다 움직이지 않는 값을 찾는 게 문제의 핵심입니다. LIS알고리즘을 통해 움직이지 않을 값을 찾을 수 있습니다. 백준 2565번: 전깃줄 문제와 유사합니다.

• 이 문제는 값을 처음 또는 끝으로만 보낼 수 있기 때문에 단순 LIS가 아니라 반드시 +1차이가 나야 합니다.
  [1, 3, 5, 4, 2]는 단순 LIS로 접근하면 [1, 3, 5]가 이미 정렬되어 있고, 각 숫자 사이에 2와 4를 넣으면 됩니다.
  하지만 처음 또는 끝으로만 값을 보낼 수 있기 때문에 [1, 2]를 그대로 두고 3, 4, 5를 움직여야 합니다.

• 아래 코드는 시간초과가 발생한 코드지만 문제의 로직을 잘 설명해 줍니다.

  import java.util.*;
  import java.io.*;
  
  public class Main {
  
      public static void main(String[] args) throws Exception {
          BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
          int N = Integer.parseInt(br.readLine());
          StringTokenizer st = new StringTokenizer(br.readLine());
          int[] arr = new int[N];
          for (int i = 0; i < N; i++) {
              arr[i] = Integer.parseInt(st.nextToken());
          }
          int[] dp = new int[N];
          Arrays.fill(dp, 1);
          int answer = 1;
          for (int i = 1; i < N; i++) {
              for (int j = 0; j < i; j++) {
                  if(arr[j]+1 == arr[i]) { // arr[i] 앞에 arr[i]보다 1 작은 값이 있으면
                      dp[i] = Math.max(dp[i], dp[j]+1);
                      answer = Math.max(answer, dp[i]);
                  }
              }
          }
          System.out.println(N-answer);
      }
  }	
  

  • i번째 값 arr[i] 앞에 만약 arr[i-1]이 있다면 arr[i-1]까지의 LIS에 +1을 한 값이 arr[i]의 LIS입니다.

• O(N^2)을 벗어나는 방법을 생각해 봅시다.
  우리는 굳이 arr[i-1]이 i번째 값보다 앞에 존재하는지 확인할 필요가 없습니다.
  존재하지 않은 상태를 0으로 표현하면 자연스럽게 arr[i]의 LIS가 정해집니다.
  순서 [1,3,5,2,4]가 주어졌을 때 i번 학생의 LIS를 나타내는 dp배열을 만듭시다.

  • 1번 학생 혼자만 있을 때 dp[1] = 1입니다.
  • 3번 학생의 LIS에는 반드시 2번 학생의 값이 필요합니다.
    하지만 2번 학생은 아직 등장하지 않았기 때문에(3번보다 뒤에있기 때문에) dp[2]의 값은 아직 0입니다. dp[3] = dp[2]+1에서 dp[2]가 0이기 때문에 dp[3]은 자연스럽게 1이 됩니다.
    +1을 하는 이유는 모든 숫자가 자기자신만 포함되어 있는 길이가 1인 LIS를 만들 수 있기 때문입니다. 1번 학생의 dp[1]이 1인 이유도 이때문입니다.

요약
숫자가 K인 학생의 LIS는 반드시 K-1번째 학생의 LIS가 필요합니다. K학생 앞에 K-1학생이 등장했는지 여부는 dp[K-1]이 0이냐 아니냐로 판단할 수 있기 때문에 굳이 검증할 필요가 없이 그냥 계산해주면 됩니다.

정답

import java.util.*;
import java.io.*;

public class Main {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());

		StringTokenizer st = new StringTokenizer(br.readLine());
		int[] dp = new int[N+1];
		int MotionLessKidsNum = 0;
		for (int i = 0; i < N; i++) {
			int num = Integer.parseInt(st.nextToken());
			dp[num] = dp[num-1]+1; // dp[num-1]이 i이전에 존재하는지 확인하지 않습니다.
			MotionLessKidsNum = Math.max(MotionLessKidsNum, dp[num]);
		}
		System.out.println(N-MotionLessKidsNum);
	}	
}