백준 9084번: 동전

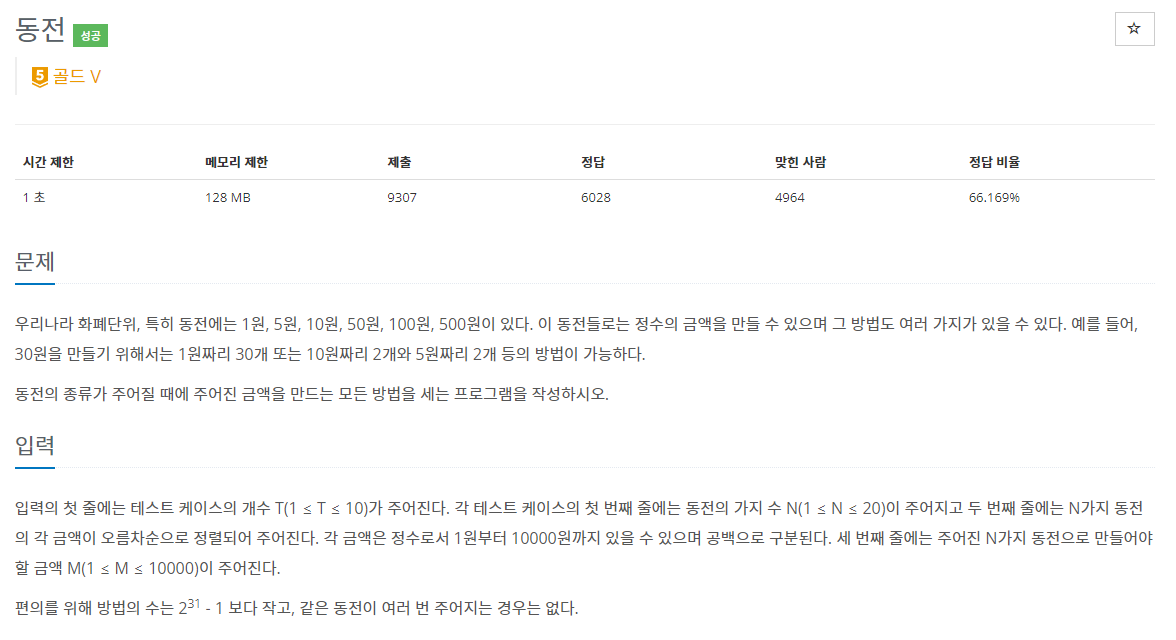
문제 설명

• https://www.acmicpc.net/problem/9084
• 동전이 N개 주어졌을 때 동전을 활용해 M원을 만드는 경우의 수를 구하는 문제입니다.

접근법

• 배낭 문제의 한 종류로 행을 동전, 열을 만들어야 하는 숫자로 두고 문제를 해결할 수 있습니다.
  배낭 문제의 핵심은 i까지 '고려'했을때의 값이 dp에 담기게 됩니다. 고려한다는 건 반드시 해당 값을 사용한다는 것과 다릅니다. dp[i][j]는 i개의 동전을 고려해 j를 만드는 경우의 수를 가지게 됩니다.

  1,5,10 3개의 동전을 이용해 11을 만드는 방법은 4가지(1*11, 1*6 + 5, 1 + 5*2, 10 + 1)입니다. 이때 (1*11, 1*6 + 5, 1 + 5*2)과 (10 + 1)를 나눠서 생각해볼 수 있습니다.
  (1*11, 1*6 + 5, 1 + 5*2)은 10이라는 마지막 동전을 사용하지 않고 만든 값입니다. 즉 dp[3][11]을 3가지 동전(1,5,10)을 이용해 11을 만드는 경우의 수라고 했을 때 dp[2][11]는 2가지 동전(1,5)을 이용해 11을 만드는 경우의 수이고, (1*11, 1*6 + 5, 1 + 5*2)은 dp[2][11]과 같습니다.
  (10 + 1)은 dp[3][1]의 경우의 수와 같습니다. 3개의 동전으로 1을 만든 뒤 10원짜리를 추가한 것이기 때문입니다.

  조금 더 일반화하면 dp[i][j] = dp[i-1][j] + dp[i][j-num]라는 점화식을 얻을 수 있습니다.

• 동전과 동일한 값이 되었을 때는 경우의 수가 하나 더 추가됩니다. 가령 5원짜리 동전 하나를 가지고 있는 상태라면 M이 0,...,4일때까지는 경우의 수가 0이지만, M이 동전의 값과 같은 5가 되면 경우의 수는 1로 변하게 됩니다. 이는 M+1길이로 만든 DP배열의 첫 Column을 1로 세팅하면 편리하게 구현할 수 있습니다. dp[i][j-num]에서 j-num이 0이 되는 경우로 1을 얻을 수 있기 때문입니다.

정답

import java.util.*;
import java.io.*;


public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int T = Integer.parseInt(br.readLine());
		StringBuilder sb = new StringBuilder();
		for (int t = 0; t < T; t++) {
			int N = Integer.parseInt(br.readLine());
			int[] arr = coinInfo(N,br);
			int M = Integer.parseInt(br.readLine());
			int[][] dp = makeDPArray(N,M);
			fillDPArray(arr,dp,N,M);
			sb.append(dp[N][M]);			
			sb.append("\n");

		}
		System.out.println(sb.toString());
	}
	
	public static int[] coinInfo(int N, BufferedReader br) throws Exception {
		int[] arr = new int[N+1];
		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 1; i <= N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}		
		return arr;
	}

	public static int[][] makeDPArray(int N, int M){
		int[][] dp = new int[N+1][M+1];
		initFirstColumn(N,M,dp);
		return dp;
	}
	
	public static void initFirstColumn(int N, int M, int[][] dp) {
		for (int i = 0; i <= N; i++) {
			dp[i][0] = 1;
		}		
	}	
	
	public static void fillDPArray(int[] arr, int[][] dp, int N, int M) {
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= M; j++) {
				int num = arr[i];
				if(j-num<0) {
                	// '선택'이 아니라 '고려'이기 때문에 이전값을 그대로 가져옵니다. 
					dp[i][j] = dp[i-1][j];
					continue;
				}
				dp[i][j] = dp[i-1][j] + dp[i][j-num];
			}
		}		
	}
}