비트연산자

개념

&: 두 피연산자의 비트값이 모두 1이면 1, 나머지는 0
|: 두 피연산자의 비트값이 모두 0이면 0, 나머지는 1
^: 두 피연산자의 비트값이 다르면 1, 같으면 0
~: 피연산자의 모든 비트를 반전
<<: 앞의 피연산자 비트열을 뒤 피연산자만큼 왼쪽으로 이동 후 빈칸은 0으로 채움
>>>: 앞의 피연산자 비트열을 뒤 피연산자만큼 오른쪽으로 이동 후 빈칸은 0으로 채움
>>: 앞의 피연산자 비트열을 뒤 피연산자만큼 오른쪽으로 이동하고 이동 후 빈칸은 음수면 1, 양수면 0으로 채움

예시

• <<

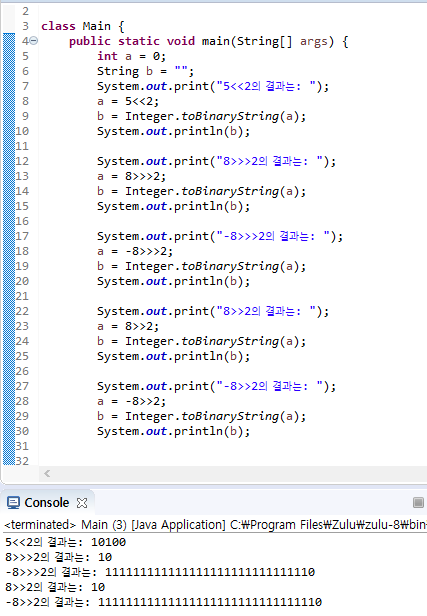
  • 5<<2
    • 00000101가 '00000101??'을 거쳐 최종적으로 00010100이 됩니다.

• >>>

  • 8>>>2
    • 00001000가 '??00001000'를 거쳐 최종적으로 00000010이 됩니다.
  • -8>>>2
    • -8을 2진수로 표현하면 11111111 11111111 11111111 11111000입니다.
    • 11111111 11111111 11111111 11111000가 '??111111 11111111 11111111 1111111000'를 거쳐 최종적으로 00111111 11111111 11111111 11111110이 됩니다.

• >>

  • 8>>2
    • 00001000가 '??00001000'를 거쳐 최종적으로 00000010이 됩니다.
  • -8>>2
    • 11111111 11111111 11111111 11111000가 '??111111 11111111 11111111 1111111000'를 거쳐 최종적으로 11111111 11111111 11111111 11111110이 됩니다.

활용

비트연산자를 다음과 같이 활용할 수 있습니다.

2진수 flag

• 2진수의 1을 true, 0을 false로 보면 2진수는 항상 어떤 boolean배열과 동일합니다.

10진수 1 == 2진수 1 == [true]
10진수 2 == 2진수 10 == [true,false]
10진수 3 == 2진수 11 == [true,true]
10진수 8 == 2진수 100 = [true,false,false] 
10진수 10 == 2진수 1010 == [true,false,true,false] 

1<<n : n번째 값

1을 왼쪽으로 n만큼 이동시킨 후 빈칸을 0으로 채웁니다.
만약 n이 3이라면
00000001이 '00000001???'을 거쳐 최종적으로 00001000이 됩니다.
1000은 n번째 자리만 1이기 때문에 n번째 값을 의미합니다. // 0번째 자리가 아니고 왜 n번째 자리냐고 의문을 가지면 복잡해서 더 이상 생각을 진행할 수 없습니다. 그냥 flat하게 느낌적으로만 받아들이시는 걸 추천드립니다.

& : 값을 확인한다

&연산은 두 값이 모두 true일때만 true를 반환합니다.
num&(1<<3)을 해 봅시다. num은 어떤 수가 들어있는지 잘 모르지만 1<<3은 00001000입니다.
num이 0이든 1이든 1<<3이 0을 반환한 곳은 무조건 0입니다.
즉 우리가 얻는 결과는 0000'?'000 입니다.
0000'0'000 혹은 0000'1'000 밖에 없습니다.
그렇기 때문에 num&(1<<3)은 num의 3번째 값을 확인하는 효과를 가집니다.
3번째 값이 0이면 0000'0'000, 3번째 값이 1이면 0000'1'000이기 때문입니다.

| : 값을 1로바꾼다(true 처리)

&와 유사합니다.
num|(1<<3)을 해 봅시다. num은 잘 모르지만 1<<3은 00001000입니다.
1<<3에서 3번째 값이 1이기 때문에 num과 무관하게 3번째 값은 true입니다.
즉 우리가 얻는 결과는 ????'1'??? 입니다.
그렇기 때문에 num|(1<<3)은 num의 3번째 값을 1(true)로 바꾸는 효과를 가집니다.

비트마스킹 순열

// 일반코드
if( isSelected[i] == true){}

// 비트마스킹 활용
if(flag &(1<<i) == 1){}

// 전체 코드
public class bitmask_permu {
	static int N,R;
	static int[] input, numbers; // input:입력수배열, numbers:선택수배열
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		R = sc.nextInt();
		
		input = new int[N];
		numbers = new int[R];
		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();
			
		}
		permutations(0,0); //실행
 				
	}
	//cnt자리의 수 뽑기
	public static void permutations(int cnt,int flag) { //flag: 뽑힌 수들에 대한 플래그비트열
		//종료 조건
		if(cnt == R) {
			System.out.println(Arrays.toString(numbers));
			return;
		}
		
		for (int i = 0; i < N; i++) {
			if((flag & 1<<i)!=0) continue; //!=말고 ==1로하면 음수일 때 문제가 생기나?
			numbers[cnt] = input[i];
			permutations(cnt+1,flag|1<<i); // 지금 내가 선택한 숫자: i번째 숫자, 그걸 사용처리(flag|1<<i)한 걸 재귀에 넘기겠다.
			
		}
	}

}

비트마스킹 부분집합

import java.util.Scanner;

public class SubSet_BinaryCounting {
		
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int[] input = new int[N];

		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();			
		}
		generateSubSet(input);
	}

	private static void generateSubSet(int[] input) {
		int N = input.length; //원소 수
		for (int flag = 0,caseCount = 1<<N; flag < caseCount; flag++) { // 1<<N == 2^N
			// flag : 원소들의 선택상태의 비트열
			for (int i = 0; i < N; i++) { // 각 비트열의 상태를 확인
				if((flag & 1<<i) != 0) {
					System.out.print(input[i]+" ");
				}
			}
			System.out.println();
		}
	}
}