카카오: 표현 가능한 이진트리

문제 설명

• 2023 KAKAO BLIND RECRUITMENT 문제 - 표현 가능한 이진트리
• https://school.programmers.co.kr/learn/courses/30/lessons/150367
• 아래 제가 적은 설명으로 문제를 이해하기가 쉽지 않습니다. 많이 생략된 내용이므로 문제를 함께 읽어보면서 직접 생각해 보시는걸 추천드립니다.
  • 어떤 수를 2진수로 변환합니다.
  • 해당 이진수를 이진트리의 노드로 생각하면 됩니다.
  • 원래의 숫자를 유지한 채 해당 이진트리를 포화이진트리로 만듭니다.
    • 원래의 숫자를 유지한다는 건 2진수의 부족한 앞부분을 0으로 채운다는 의미입니다. 채우는 건 숫자에 영향을 주지 않습니다. 00001과 1은 10진수로 변환했을 때 같은 값입니다.
    • 포화이진트리는 노드의 총 개수가 항상 ((2^x)-1)개 입니다.
  • 각 노드를 검사합니다. 자신이 1인데 부모가 0이면 모순입니다.

접근법

문제의 대략적인 형태는 금방 파악할 수 있었지만 모호한 조건이 많았습니다. 결과적으로 부모가 0인데 1의 자식을 가지는 모순이 발생하는 경우만 0, 그렇지 않으면 1을 반환해야 했습니다.

애매했던 부분
자식도 0이고 부모도 0이면 조건을 만족하는걸까? 만족합니다.
포화이진트리를 만들 때 반드시 0을 앞으로 채워야할까? 앞으로만 채워야 합니다.

전체 흐름은 다음과 같습니다.
1. 입력값을 2진수로 만듭니다.
2. 2진수를 포화이진트리로 만듭니다. 2진트리는 반드시 ((2^n) - 1)개의 노드를 가집니다.
조금 더 정확히는 이진트리의 height를 구한 뒤 해당 height의 포화이진트리가 가져야 할 부족한 노드개수만큼을 앞에서부터 0으로 채워줍니다.
3. 포화이진트리에서 부모를 찾아가는 방법을 구합니다.
4. 부모가 0인데 자식이 1인 모순이 존재하는지 파악합니다.

3번을 구현하는 게 가장 어려웠습니다. 트리의 속성을 완벽히 이해하고 값을 구했다기 보다 특정 규칙을 갖는 수열을 구현하는 느낌의 풀이가 되어버렸습니다.
저는 vectorToGoParent[i] = i번째 노드가 부모로 가기 위해 움직여야 하는 값으로 구했습니다. 즉, i + vectorToGoParent[i] = 부모노드 index가 형성됐습니다. vectorToGoParent는 재귀적인 성질을 가집니다. 먼저 방향(부호)을 고려하지 않았을 때 다음과 같은 규칙을 가집니다.

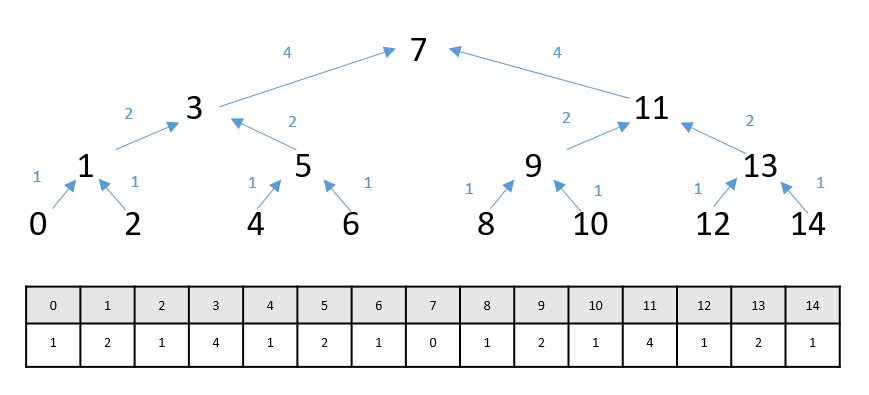
• 리프노드의 height를 0이라 할 때 각 계층의 노드는 자신의 부모로 가기 위해 2^height만큼의 이동이 필요합니다.

방향을 고려하면 우측노드는 부모로 가기 위해 해당 거리만큼 -값을 가져야 합니다. 즉 최종적으로 높이가 3인 포화이진트리는 [1,2,-1,4,1,-2,-1,0,1,2,-1,-4,1,-2-1]모양의 vectorToGoParent배열을 가져야 합니다. 저는 이를 재귀함수로 구현했습니다. String으로도 도전해보고 ArrayList로도 도전해봤는데 다 실패하고 결국 아래와 같은 코드가 나왔습니다. 대략 N번째 값 = N-1번째 값 + 부모노드 + N-1번째 값형태의 재귀코드입니다.
저는 특히 우측노드를 -처리하는 게 특히 어려웠습니다. 정확히는 이전 재귀에서 다른 값의 부호는 이미 처리되었기 때문에 우측노드의 root만 -처리해줘야 합니다. center + (int)Math.pow(2,depth-2)는 N-1번째 재귀함수의 center값입니다. N-1번째 재귀함수의 center값의 부호만 -로 바꿔줬습니다. 이때 if(depth > 1)라는 조건을 걸었는데 높이가 0인 1을 만들 때 덮어쓰기 되어버리기 때문에 모든 1의 값의 부호가 반대로 나와버려서 이러한 조건을 붙였습니다.
특별한 코드라기보다는 제가 해당 알고리즘을 효율적으로 구현하지 못해서 생긴 문제 정도로 이해해 주시면 될거 같습니다.

정답

import java.util.*;

public class Main {
	public static void main(String[] args) throws Exception {
		long[] numbers = new long[] {63,111,95};
		int[] answer = new int[numbers.length];		
		for (int i = 0; i < numbers.length; i++) {
			String s = Long.toBinaryString(numbers[i]);			
			String perfectBinaryTree = makePerfectBinaryTree(s)[1];
			int height = Integer.parseInt(makePerfectBinaryTree(s)[0]);		
			int centerIdx = ((int)Math.pow(2, height)-1)/2;
			int[] vectorToGoParent = new int[(int)Math.pow(2, height)-1];
			calVectorFromChildToParent(height,vectorToGoParent,centerIdx);
			vectorToGoParent[centerIdx] = 0;
			if(isCorrect(perfectBinaryTree,vectorToGoParent)) {
				answer[i] = 1;
			}
		}
		System.out.println(Arrays.toString(answer));
	}
	
    // 포화이진트리 만들기
	public static String[] makePerfectBinaryTree(String binaryNumber) {
		int length = binaryNumber.length();
		int height = findHegihtOfPerfectBinaryTree(length);
		StringBuilder padding = new StringBuilder();
		for (int i = 0; i < Math.pow(2, height)-1-length; i++) {
			padding.append("0");
		}
		padding.append(binaryNumber);
		return new String[]{Integer.toString(height),padding.toString()};
	}
	
    // 2진수의 문자열의 길이를 통해 포화이진트리의 높이 구하기.
	public static int findHegihtOfPerfectBinaryTree(int length) {
		for (int i = 0; i < 100; i++) {
			if(Math.pow(2, i)-1 <= length && length < Math.pow(2, i+1)) {
				return i+1;
			}
		}		
		return -1;
	}
	
    // 포화이진트리의 부모노드 인덱스로 가기 위해 이동해야 하는 값
	public static void calVectorFromChildToParent(int depth, int[] arr, int center) {
		if(depth == 0) return;
		calVectorFromChildToParent(depth-1,arr,center - (int)Math.pow(2, depth-2));
		arr[center] = (int)Math.pow(2, depth-1);
		calVectorFromChildToParent(depth-1,arr,center + (int)Math.pow(2, depth-2));
		if(depth > 1) {
			arr[center + (int)Math.pow(2, depth-2)] *=-1;
		}		
	}

	// 부모가 0인데 1인 자식이 존재하는 오류가 있는지 검사
	public static boolean isCorrect(String perfectBinaryTree, int[] vectorToGoParent) {
		for (int i = 0; i < perfectBinaryTree.length(); i++) {
			if(perfectBinaryTree.charAt(i) == '1' && perfectBinaryTree.charAt(i+vectorToGoParent[i]) == '0') return false;
		}
		return true;
	}	
	
	

}