DP에 대한 내용을 정리하기 전에!

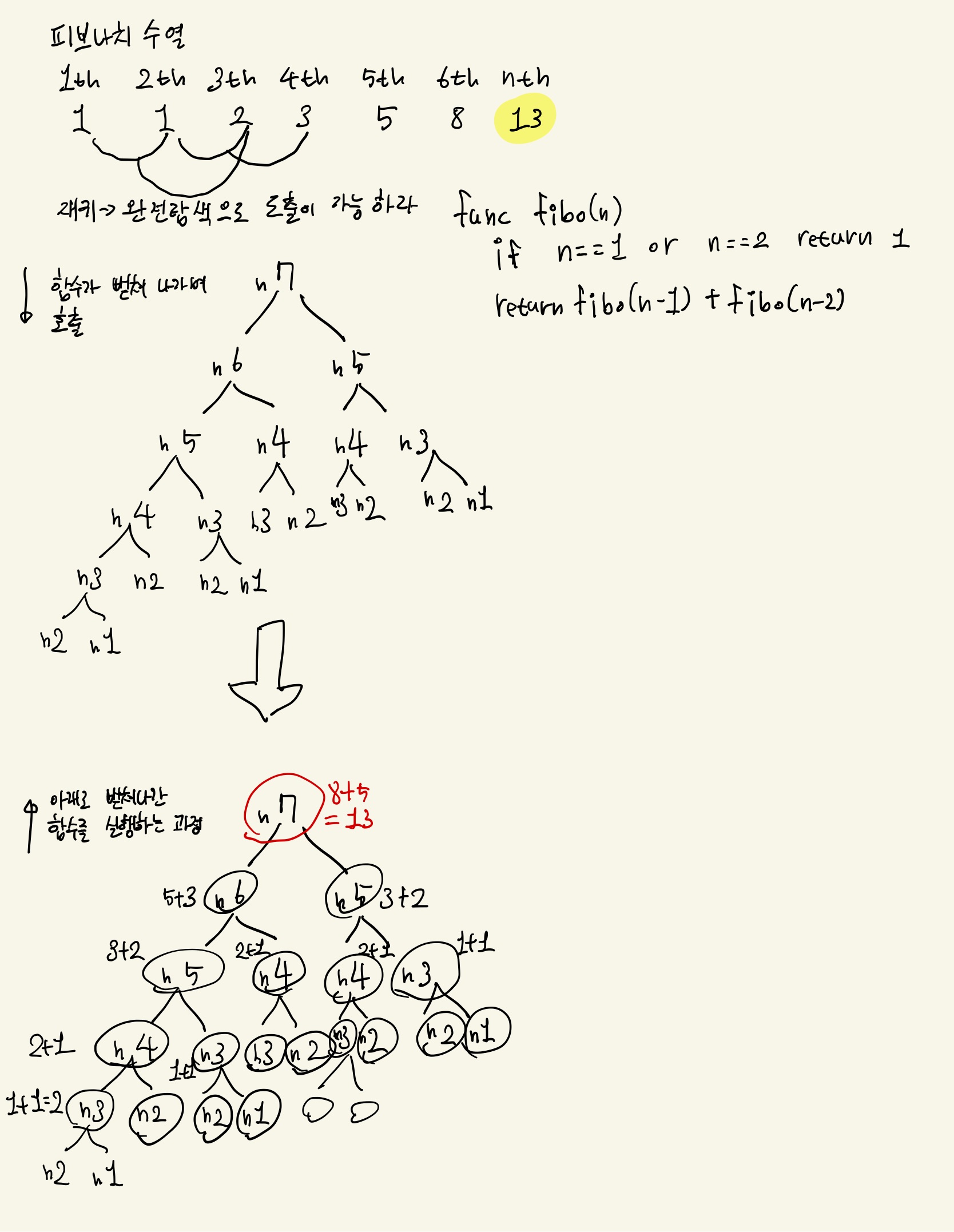
재귀에 대해 다시 정리하자

• 접근방법 > 완전탐색(재귀)
• 크고 복잡한 문제를 하위 문제로 나눈다.
• 하위 문제에 대한 답을 계산한다.
• 하위 문제에 대한 답으로 원래 문제에 대한 답을 계산한다

대표적으로 피보나치 수열을 구하는 문제를 예시로 들어보자

• 굉장히 많은 함수가 호출이 된다 ! ( 시간 복잡도 : O(2n) )
• 이미 계산해 놓은 값도 다시 계산하여 비효율 적이다.
• 말 그대로 완전 탐색의 과정을 거친다고 이해할 수 있겠다.

const fibo = (n) => {
  if (n <= 1) {
    return n;
  } else {
    return fibo(n - 1) + fibo(n - 2);
  }
};

console.log(fibo(7));

//13

• 자바스크립트로 피보나치 수를 구현한 대표적인 예시이다. 내가했음

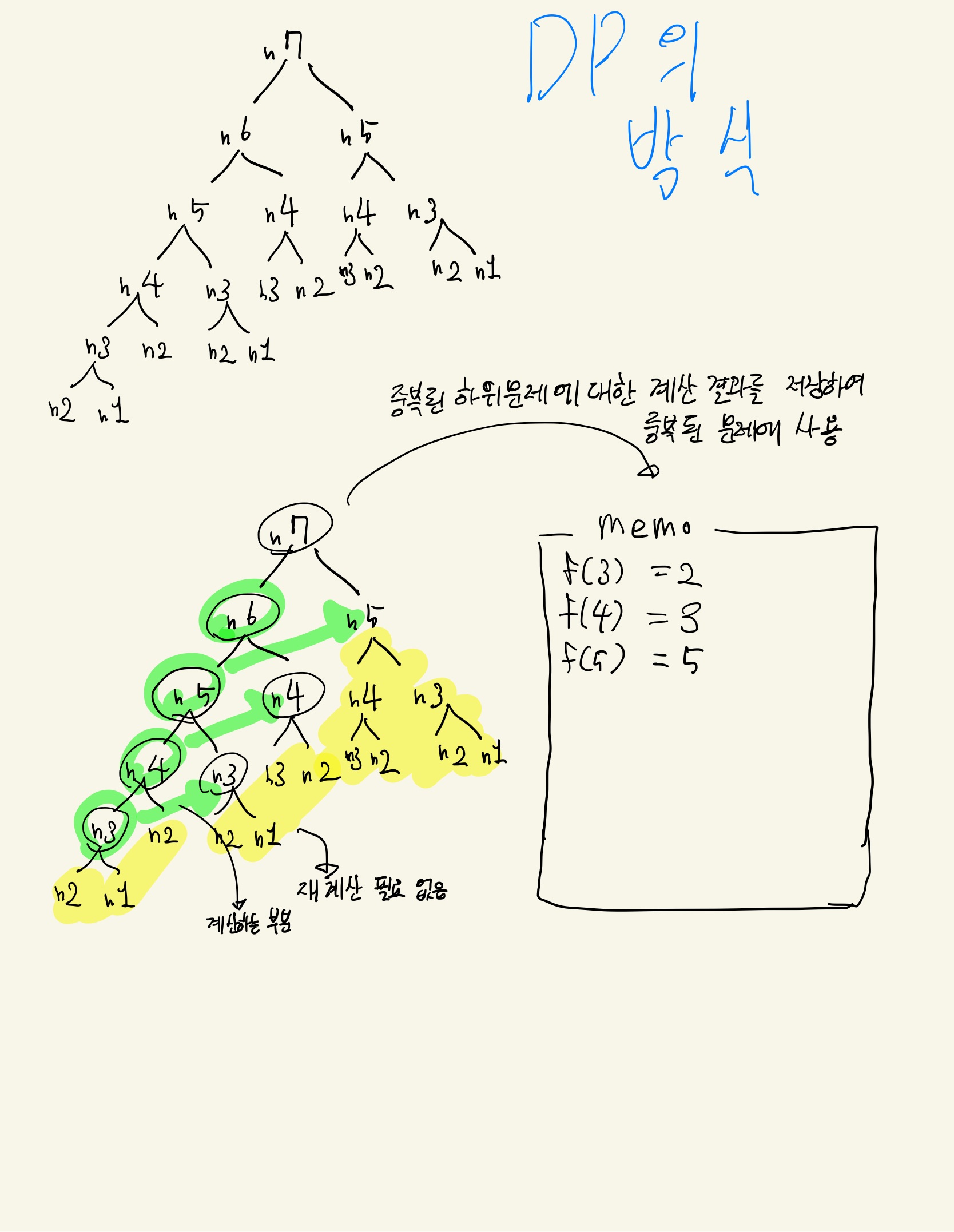
그래서 DP를 쓰는 이유가 ?

• 접근방법 > 완전탐색(재귀) > DP
• 크고 복잡한 문제를 하위로 나눈다 ( 재귀와 (성)동일 )
• 하위 문제에 대한 답을 계산 후 중복 메모리에 대해선 저장해 놓은 값을 쓰자! ( 시간복잡도 : O(n) )
• 하위 문제에 대한 값으로 원래 문제에 대한 답을 계산한다 ( 재귀와 동일 )

DP의 특징

• 재귀적인 형태로 Top-down의 형태를 띈다
• 가장 큰 문제에서 작은 문제로 하나하나 쪼개가기 때문에 ( 그러나 본격 계산은 아래부터 하긴 한다 )

let memo = [];
let fibo = (n) => {
  if (n < 3) {
    memo[n] = 1;
  }
  if (!memo[n]) {
    // 내가 저장한 값 중에 없다면 
    memo[n] = fibo(n - 1) + fibo(n - 2);
        // 재귀를 이용해 구하고 저장
  }

  return memo[n];
};

console.log(fibo(7));

//13

• 배껴왔음

이 정도로 다뤄보고 문제 풀이로 돌아온다