
순열이란 ?
주어진 정수를 조합하여 모든 경우의 수를 나열하는 것!
단순 반복문을 이용해서도 구현할수 있지만 재귀에 익숙해지기 위해 재귀로 구현하는 방법을 선택해서 구현했습니다.
[1, 2, 3]의 배열의 수현을 구하려면 어떡해야 할까 생각해 보았을때
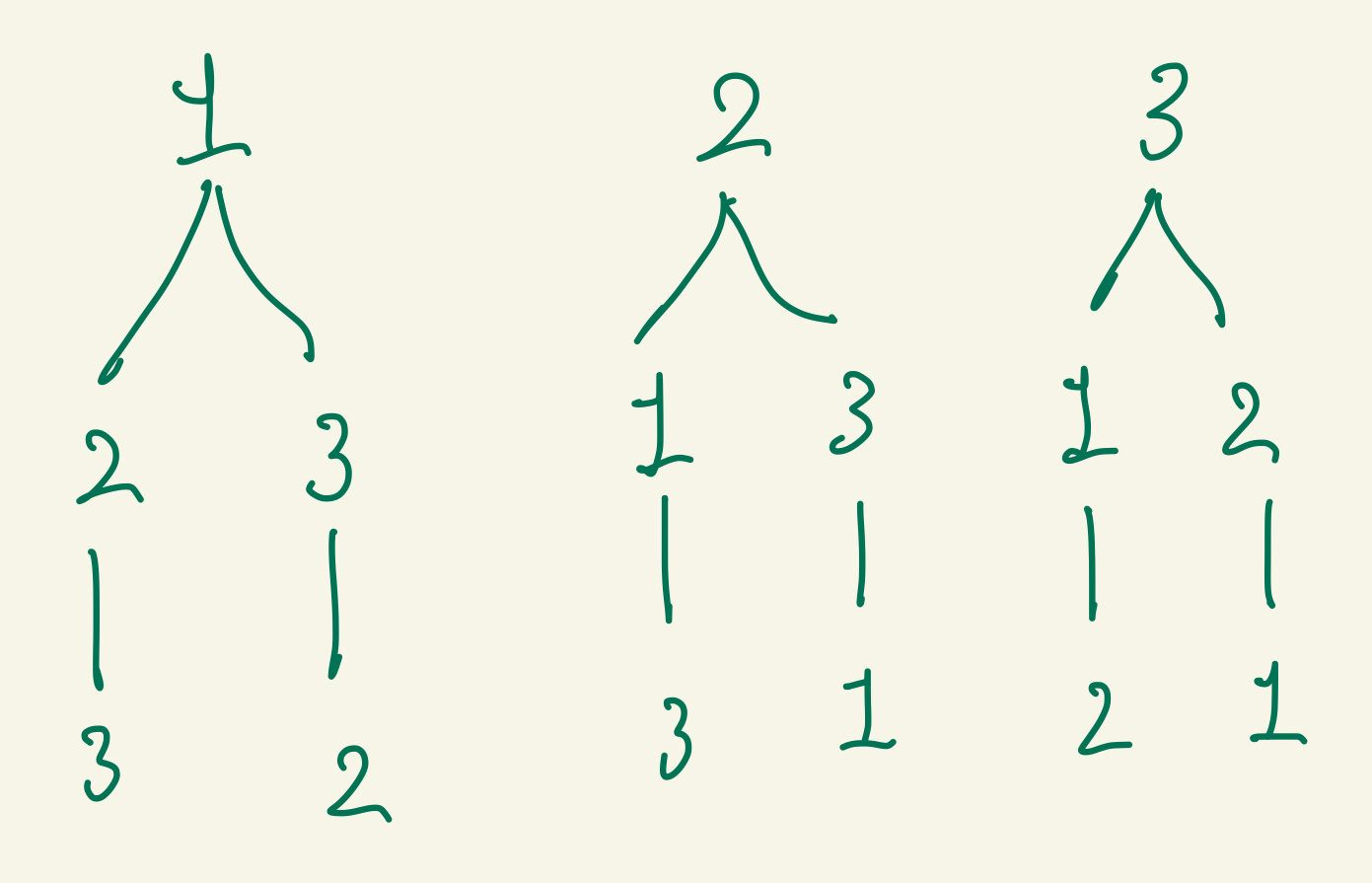
이런식으로 그림을 그려볼수 있고
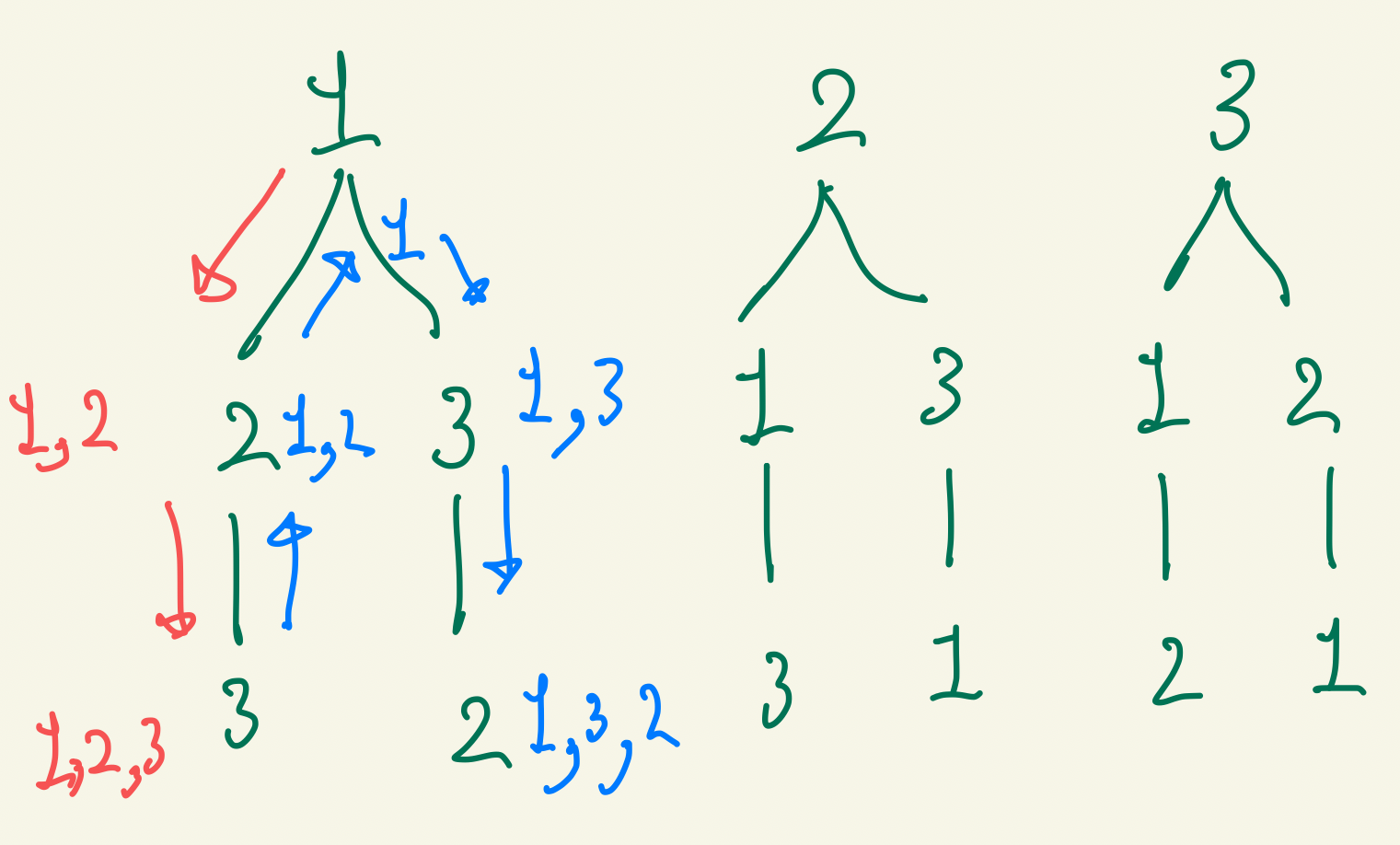
빨강 > 파랑의 순서로 생각해서 이 과정을 반복하면 몇개의 수가 나와도 순열이 구현됩니다.
여기서 요구하는 순열의 길이에 따라 재귀의 베이스케이스를 조절해주면 됩니다.
주어진 수의 갯수와 동일한 길이의 수열을 반환하는 코드를 구현해봤습니다 !
const solution = (nums) => {
const result = [];
const cur = [];
const backtrack = (cur) => {
if (cur.length === nums.length) {
result.push([...cur]);
return;
}
for (const num of nums) {
if (!cur.includes(num)) {
cur.push(num);
backtrack(cur);
cur.pop();
}
}
};
backtrack(cur);
return result;
};
console.log(solution([1, 2, 3, 4]));코드 설명
if (cur.length === nums.length) {
result.push([...cur]);
return;
}재귀의 베이스케이스가 될 것이고 길이가 주어진 배열의 길이와 동일해지면 함수를 중단하고,
위 그림으로 치면 파랑색 화살표의 로직을 진행해줍니다.
for (const num of nums) {
if (!cur.includes(num)) {
cur.push(num);
backtrack(cur);
cur.pop();
}
}여기선 주어진 배열을 탐색하는데 [1, 1, 1, 1]은 수열이 될수 없기 때문에 includes메서드를 이용하여 지금 탐색하는 수가 이미 있는 경우에는 배열에 요소를 추가해주지 않습니다.
그렇게 cur에는 지금 탐색중인 요소를 담아주고 result에는 cur이 베이스케이스에 만족할 시 해당 배열을 담아줍니다 !
위의 예시로 보자면 [1, 2, 3], [1, 3, 2], [2, 1, 3]....이런 순서로 배열에 담기겠죠 !
cur의 상태를 보자면
[1]
[1, 2] cur push
[1, 2, 3] result push
[1, 2] cur pop
[1] cur pop
[1, 3] cur push
[1, 3, 2] result push이런 순서로 진행되는것 까지 확인할수 있습니다.
여기서 생각해볼 부분은..
재귀를 진행하면서 nums를 탐색하는데 nums가 길어질수록 CallStack에 너무 많은 함수가 쌓일수 있다는 점입니다.
고민해보겠습니다.
조합은 ?
조합을 구현할 땐 위 순열과 다르게 중복되지 않아야 한다는 점이 중요합니다.
[1, 2, 3, 4], [2, 1, 3, 4]
이 둘은 순서는 다르지만 중복되는 요소들이기 때문에 중복된다고 볼수 있고,
순열과의 가장 큰 차이는 순열은 가능한 모든 경우의 수를 나열하지만,
조합은 여기서 한번 더 걸러줘야하는 점이 있는거죠 !
하나 더 생각해야할 것은 위에서 구현한 수열의 경우에는 주어진 요소들의 길이와 동일한 길이로 구현했습니다.
조합은 그렇게 구현하면 당연히 하나밖에 나오지 않기 때문에 길이를 임의로 지정해줘야 합니다 !
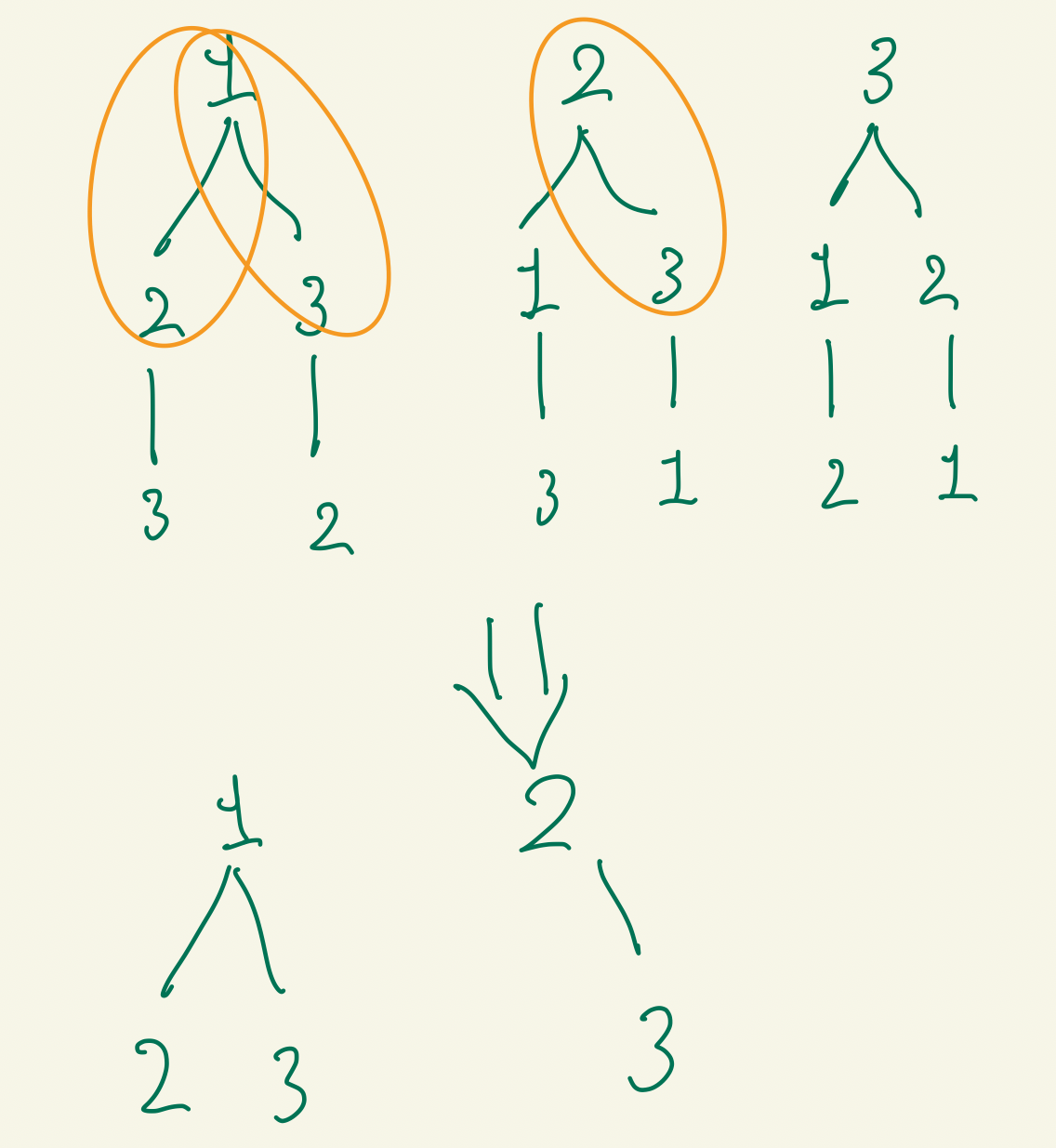
2개로 중복되지 않는 조합의 예시를 그려봤을때..
지금 가지고 있는 요소에서 1을 더해준 것만 탐색해주면 된다는 것을 확인할수 있습니다 !
구현 방식은 거의 동일합니다 !
const solution = (nums, end) => {
const result = [];
const cur = [];
const backtrack = (cur, start) => {
if (cur.length === end) {
result.push([...cur]);
return;
}
for (let i = start; i < nums.length; i++) {
cur.push(nums[i]);
backtrack(cur, i + 1);
cur.pop();
}
};
backtrack(cur, 0);
return result;
};
console.log(solution([1, 2, 3, 4], 2));차이점이 보이시나요 !
start라는 변수를 하나 만들어주고 다음 숫자만 탐색하도록해주어서 간단한 조합도 구현할수 있었습니다..
파이썬은 제공하는 라이브러리가 있다고 하는데 부럽군요
하지만 이렇게 직접 구현해보는 경험은 좋았습니다 !
앞으로 조합 관련된 문제도 풀어보며 공부해야겠어요 그럼 20000...
