[TIL] 24.10.27 SUN

삼각비

삼각비는 직각삼각형 변들 사이의 비율을 이용하여 각도와 변의 길이를 구하는 방법이다. 우리가 삼각함수에서 사용하는 Sin, Cos, Tan 모두 삼각비의 일종이다.

밑변과 높이?

우리가 학창시절 삼각함수를 배울 때 높이를 밑변으로 나눈게 탄젠트, 높이를 빗변으로 나눈게 사인 등등 이런식으로 외웠었는데 밑변과 높이에 대한 기준이 중요하다.

원하는 각도에 따라 밑변과 높이는 달라지기 때문이다.

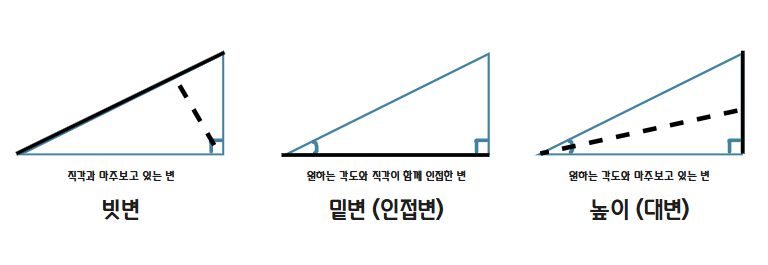
빗변은 직각과 마주보고 있는 변이다.
높이(대변)는 원하는 각도와 마주보고 있고, 직각과는 인접하지 않은 변이다.
밑변(인접변)은 원하는 각도와 직각이 함께 인접한 변이다.

sin, cos, tan

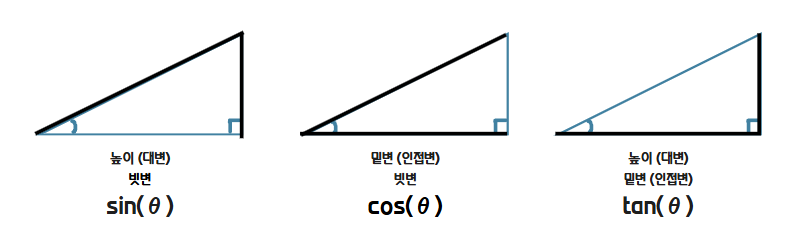
sin

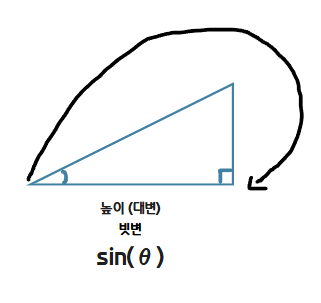
사인은 삼각형에서 주어진 각도의 마주보는 변인 높이(대변)을 빗변으로 나눈 것이다.

사인의 유래는 고대 인도 수학에서 아르다-자야라고 불렸고 이는 반원 호를 뜻한다. 12세기 유럽으로 전파될 때 라틴어 sinus(곡선, 만곡) 이라는 뜻을 가진 단어가 사용되었고 이게 지금은 sin이 된 것이다.

cos

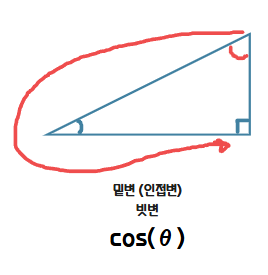
코사인은 사인의 보수라는 의미에서 유래되어 원하는 각도(θ)와 그 보각 90-θ 이 있을 때 해당 보각의 사인이 코사인이다.
즉 , cos(θ) = sin(90-θ)을 뜻한다.

tan

탄젠트는 접하다라는 뜻의 라틴어 tangens에서 유래되었으며 단위원에서 특정 각도에 대한 탄젠트 값은 원의 접선과 관련된 길이로 해석할 수 있다.

특수각에 관련된 삼각형

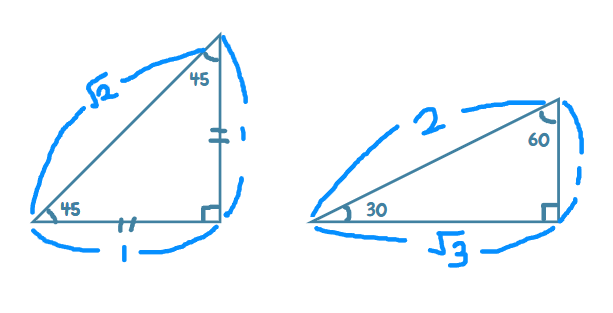
우리가 중학 수학때 배운 특수각에 관련된 삼각형은 직각삼각형과
직각삼각형이면서 이등변이 같은 삼각형이 있다.

피타고라스 정의에 따른 비율은 위의 그림과 같다.
그럼 특수각 (30, 45, 60) 에 대한 사인, 코사인, 탄젠트의 값 또한 구할 수 있다.

	$30°$	$45°$	$60°$
$sin$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$
$cos$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$
$tan$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$

단위원과 삼각함수 정의의 관계?

삼각함수의 정의는 단위원과 직각삼각형의 기하학적 성질에서 자연스럽게 도출된다.

단위원

단위원은 반지름이 1인 원을 말한다.
원점(0,0) 을 중심으로 하고 반지름이 1이기 때문에
$x^2+y^2 = 1$ 같은 방정식을 가진다.

예를들면 아래와 같다.
$θ=0°$일 때 (1,0)
$θ=90°$일 때 (0,1)
$θ=180°$일 때 (-1,0)

단위원과 직각삼각형의 관계

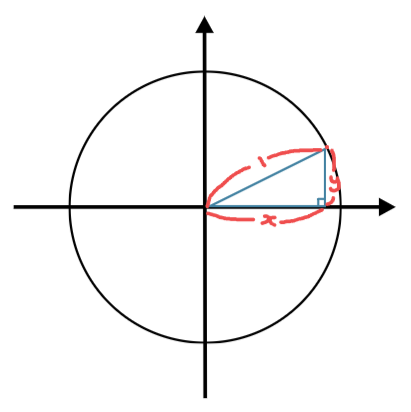
여기서 다르게 해석하면 단위원은 직각삼각형이 형성된다고 볼 수 있다.
x축은 인접변, y축은 대변, 반지름(1)은 빗변

우리가 아까 배운 삼각비에 따르면,
$cos(θ) = \frac{x}{1} = x$
$sin(θ) = \frac{y}{1} = y$

즉, 각도 θ 에 대한 단위원의 점 좌표는
$(x,y) = (cos(θ),sin(θ))$ 이다.

그렇다면 우리는 다음과 같이 정의할 수 있다.

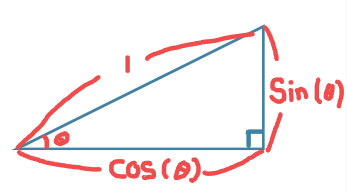
빗변이 1일때, x값은 코사인 y값은 사인이다.
탄젠트는 무엇을 의미하는가?

$tan(θ) = \frac{sin(θ)}{cos(θ)}$

$특정 θ에 대한 동경의 기울기 = \frac{y}{x}$

$즉, 동경의 기울기 = \frac{sin(θ)}{cos(θ)} = tan(θ)$

탄젠트는 세타에 대한 동경의 기울기라고 할 수 있겠다.

각도와 거리로 좌표 구하기

원점에서 특정 각도 θ 방향으로 거리 r만큼 떨어진 곳의 좌표를 구하고자 할 때 우리는 다음과 같이 정의할 수 있다.
$x = r * cos(θ)$
$y = r * sin(θ)$

만약 45도 방향으로 10정도의 거리가 떨어진 적의 위치를 구하고자 한다면,
$x = 10 * cos(45) = 10 * \frac{\sqrt{2}}{2} ≈7.07$
$y = 10 * sin(45) = 10 * \frac{\sqrt{2}}{2} ≈7.07$

현 위치 (10,20)에 있을 경우 적의 좌표는 $(17.07,27.07)$ 이라고 할 수 있다.