Union-Find

• union-find는 disjoint set을 이용 대표적인 그래프 알고리즘
• uses:
  1. 그래프에서 서로 연결되어 있는 node들을 찾기
  2. 그래프에서 cycle이 발생하는지 확인 (kruskal algorithm)

Vocabulary

• Disjoint set:
  • two distinct sets with no common elements
  • 공통원소가 존재하지 X (상호 배타적인 부분집합들)
  • 아래 왼쪽 그림처런 공통원소가 없는 상태:
    
• Union: disjoint set을 하나의 집합으로 합치는 것
• Find: 찾고자 하는 원소 x가 들어 있는 집합을 찾는 것

characteristics

• each set is represented as a tree
• time complexity: O(log N)
  - since we are using a tree
  • BUT 원소들이 하나의 트리로 몰리게 되면 O(N)이 될 수 있음 --> path compression, rank를 이용해서 최적화

기본 구현

int parent[MAX];

void init(){
	for(int i = 0; i < MAX; ++i)
    	parent[x] = x; // 각각 자기 자신만 존재하는 set 구성
}

int find(int x) {
    if (x == parent[x])
        return x;
    else
    	return find(parent[x]);
}

void union(int a, int b){
	int rootA = find(a);
    int rootB = find(b);
    
    parent[rootB] = rootA; // b's root connected to a's root
}

Union-by-rank

• rank = tree depth
• higher rank tree added to lower rank tree
• 이런 방식으로 트리들을 합치게 되면 더웃 효율적이게 관리 가능

code

void union_find() {
    int a, b;
    cin >> a >> b;

    int rootA = find(a);
    int rootB = find(b);

    if (rootA == rootB)
        return;


    if (node_rank[rootA] < node_rank[rootB]) {
        parent[rootA] = rootB;
    } else if (node_rank[rootA] > node_rank[rootB]) {
        parent[rootB] = rootA;
    } else {
        parent[rootB] = rootA;
        ++node_rank[rootA];
    }
}

Path compression

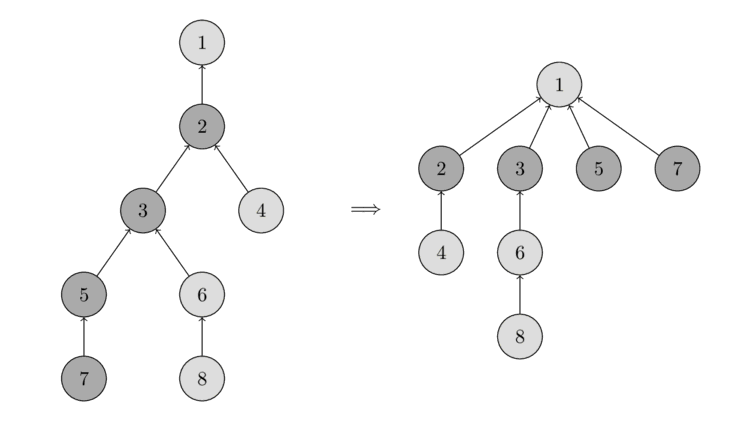
• tree height를 줄이면 find를 할때 필요한 연산이 줄어들게 된다
• 아래 그림처럼 노드들을 직접 root에 달아서 find할때 필요한 traversal을 줄임
• root node를 원하는 값으로 강제할 수 있다
  
  

code

int find(int x) {
    if (x != parent[x])
        parent[x] = find(parent[x]); // flatten the tree

    return parent[x];
}

참고자료

• union-find: what does it do
• disjoint set img
• union by rank img
• path compression img1
• path compression img2